Электромагнитные колебания

Электромагнитные колебания

 

Общие сведения о колебаниях

 

Колебания - это процесс, при котором физические величины, характеризующие его, периодически изменяются во времени: по истечении времени, кратного периоду t = nT (T - период колебаний, n = 1, 2, 3,...), любая из этих величин (X) приобретает первоначальное (t = 0) значение. За единицу времени совершается число колебаний n = 1/T, n - частота колебаний. Наряду с n используется также круговая частота w = 2pn, которая равна числу колебаний за время, равное 2p(сек):

w = 2p/T.

Колебания называются гармоническими, если X изменяется по закону косинуса:

X = A cos (wt + a) (1)

A - амплитуда колебаний, которая равна максимальному значению X;

(wt + a) - фаза колебаний, имеющая смысл угловой меры времени;

a - начальная фаза, определяющая в соответствии с (1) значение X в момент времени t = 0.

Независимо от природы гармонические колебания описываются одними и теми же дифференциальными уравнениями и подразделяются на несколько типов.

 

Свободные незатухающие колебания описываются однородным дифференциальным уравнением второго порядка

d²X/dt² + w₀²X = 0. (2a)

Решение этого уравнения

X = A cos (w₀t + a), (2б)

w₀ - собственная частота колеблющейся системы, которая определяется внутренними (собственными) параметрами. К примеру, w₀² = k/m для пружинного маятника, где k – коэффициент жесткости пружины, m - масса тела, x – смещение массы m от положения равновесия; сила упругости F = - kx. Для математического маятника при малой амплитуде колебаний в роли квазиупругой силы, возвращающей маятник к положению равновесия, выступает составляющая силы тяжести mg и w₀² = g/ l, где g - ускорение свободного падения, l - длина маятника. В колебательном электрическом L-C контуре w₀² =1/LC, где L – индуктивность, С - электрическая емкость.

 

Свободные затухающие колебания описываются уравнением

d²X/dt² + 2bdX/dt + w₀²X=0. (3a)

Его решение - при w₀² > b² (b - коэффициент затухания)

X = A₀e^-bt×cos(wt+a). (3б)

Собственная частота и период затухающих колебаний

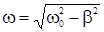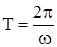, ^. (3в)

Отметим, что период затухающих колебаний тем меньше, чем больше величина затухания b.

Появление в ур. (3а) члена 2bdX/dt обусловлено учетом диссипативных сил, в присутствие которых энергия, запасенная в колеблющейся системе, постепенно переходит в тепло.

Величину A=A₀e^-bt можно назвать амплитудой затухающих колебаний, которая, как видно, уменьшается со временем по экспоненциальному закону. На рис.1 и 2 приведены зависимости X(t), соответствующие ур. (2б) и (3б).

 

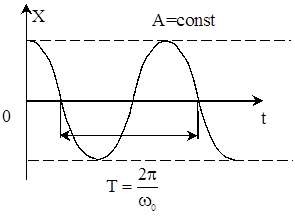
Рис. 1. Рис. 2.

 

Заметим, что квадрат амплитуды колебаний пропорционален энергии системы (механической или электрической) и уменьшение амплитуды связано с переходом этой энергии в тепло. Затухание колебаний принято описывать посредством нескольких параметров.

Декремент затухания:

e^bT = A(t)/A(t+Т)= 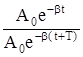(4)

Логарифмический декремент затухания:

l =ln[A(t)/A(t+Т)] = bT (5)

Выразив согласно ур.(5) b через l, закон убывания амплитуды со временем можно представить как:

A = A₀ (6)

Временем релаксации t называется время, в течение которого амплитуда колебания уменьшается в e раз (т.е. при 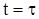имеем А/А₀=e^-lt/T=e^-1), .

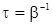За время t система совершает число колебаний N_t=t/Т.

Следовательно, lt/T=lN_t=1 и логарифмический декремент затухания по величине обратно пропорционален N_t

l = 1/ N_t. (7)

Кроме l, колебательная система может быть охарактеризована добротностью Q:

Q = p/l = p N_t. (8а)

Можно показать, что добротность Q при слабом затухании (b < w₀) равна отношению энергии колеблющейся системы в любой момент времени t к ее убыли за период, т.е.

Q/2p = W(t)/[W(t) - W(t+T)] (8б)

Заметим в заключение, что при сильном затухании, т.е. при b² > w₀², колебания не возникают - процесс является апериодическим. Для такой системы зависимость X(t) имеет вид кривых 1 или 2, приведенных на рис.3. При этом кривая 2 наблюдается в случае, когда система выведена из равновесия за счет сообщения ей достаточно большой энергии.

Рис. 3.

 

Вынужденные колебания.

Этот вид колебаний возникает, если система подвергается внешнему периодическому воздействию, например, силы в механической системе или напряжения в электрической, изменяющихся по гармоническому закону:

F = F₀ coswt или U = U₀ coswt.

Уравнение вынужденных колебаний имеет вид:

d²X/dt² + 2bdX/dt + w₀²X = Ycoswt, (9)

где через Y обозначены величины F₀/m для механической системы или U₀/L для электрической цепи соответственно; w₀ , как и выше, имеет смысл собственной частоты колебаний системы, т.е. в отсутствие внешнего периодического воздействия и диссипативных сил.

Уравнение (9) является неоднородным дифференциальным уравнением и его общее решение равно сумме общего решения соответствующего однородного уравнения - (3а) и частного решения данного неоднородного ур.-(9).

Поскольку общее решение ур.(3а) описывает затухающие колебания (см. далее ур.(3б)), то по истечении некоторого времени (тем большего, чем меньше коэффициент b) собственные колебания затухают и система переходит в режим вынужденных колебаний с частотой вынуждающей силы w:

X = A cos (wt - j), (10)

фаза которых отличается от фазы внешнего воздействия на j. Это выражение является частным решением ур.(9), следовательно, в ур.(9)

dX/dt = - w A sin (wt - j) = wA соs(wt - j + p/2), (11)

d²X/dt² = - w²A cos(wt - j) = w²A cos(wt - j + p).

Подставив (10) и (11) в ур.(9), получим

w²A cos(wt - j + p) + 2bwA cos(wt - j + p/2) + w₀²A cos(wt - j) = Y₀ coswt (12)

Поскольку все слагаемые ур-я (12) являются гармоническими функциями, то определить амплитуду и фазу вынужденных колебаний можно методом векторных диаграмм. Это графический метод, при котором колебание изображается в виде вектора, выходящего из точки О, его модуль равен амплитуде колебания А, а угол наклона к оси Х – фазе (wt + a) (см. рис.4 и ур.(1)). При вращении этого вектора вокруг точки О его проекция на ось Х равна A cos (wt + a), т. е. совпадает с выражением (1).

С помощью метода векторных диаграмм можно складывать гармонические колебания с одинаковыми частотами. Для этого колебания-слагаемые изображаются в виде векторов, выходящих из одной и той же точки О. Их взаимная ориентация на плоскости определяется начальными фазами. Векторы-слагаемые ур. (12) показаны на рис.5а (w₀ > w) и 5б (w₀ < w); их начальные фазы – (), () 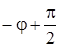и т.д. В каждый момент времени, включая t=0, вектор Y₀ будет равен векторной сумме векторов-слагаемых левой части ур.(12).

Соотношение фаз слагаемых левой части ур.(12) позволяет определить A и j из рис.5а,б по теореме Пифагора:

. (13)

Откуда

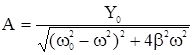, (14)

tg 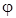= 2bw/(w₀² - w²). (15)

А) б)

Рис. 4. Рис. 5.

Резонанс.

Амплитуда вынужденных колебаний системы зависит, как видно из ур.(14), от частоты внешнего воздействия w. Если изменять величину w, то при некотором ее значении w = w_р амплитуда вынужденных колебаний приобретает максимальное значение A = A_р. Это явление называется резонансом. Квадрат амплитуды определяет энергию колеблющейся системы, следовательно, при приближении к резонансу (w w_р) она возрастает. Однако энергия может увеличиваться только за счет работы, совершаемой при внешнем воздействии. Следовательно, при резонансе существуют наиболее благоприятные условия для передачи энергии в колеблющуюся систему извне, т.е. выполнения положительной работы. Возрастание амплитуды вынужденных колебаний до величины A_р - это процесс передачи энергии системе извне, который длится конечное время. В связи с этим нужно иметь в виду, что даже очень резкое увеличение амплитуды при резонансе, которое имеет место при малом затухании b, не происходит мгновенно. Для электромагнитных систем (настройка приемника) это время много меньше, чем для механических (раскачивание качелей); заметим, что мгновение для наблюдателя, настраивающего приемник, является громадным временем по сравнению, например, со временем жизни возбужденного атома (10^-8 сек).

После того, как установилось значение амплитуды A = A_р = const, вся энергия, поступающая в систему извне, расходуется на работу против диссипативных сил.

Рассчитаем резонансную частоту, потребовав при этом, чтобы в ур.(14) величина А имела максимальное значение. Это выполняется, если значение знаменателя минимально. Продифференцировав и приравняв нулю выражение знаменателя ур.(14), имеем:

- 4(w₀² - w²)w + 8b²w = 0. (16)

Ур.(16) имеет три решения: w = 0 и w = ± 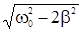. Первое из них соответствует не максимуму, а минимуму амплитуды. Отрицательное значение частоты не имеет физического смысла, поэтому

w_р = + 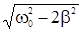. (17)

Отсюда

(18)

На рис.6 представлены резонансные кривые - зависимости амплитуды от частоты внешнего воздействия - A(w) при различных значениях параметра b. При 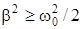явление резонанса исчезнет (нижняя линия на рис.6). Величина j (ур.15) изменяется от 0 до p (рис.7).

На рис.6 видно, что чем меньше затухание (b), тем резче увеличивается амплитуда А_р и тем ближе значение w_р к w₀ (собственной частоте незатухающих колебаний). При w ® ¥ все кривые асимптотически стремятся к нулю, т.е. система не успевает реагировать на внешнее воздействие, а при w ® 0 на нее действует постоянная внешняя сила, т.е. колебания тоже не возбуждаются.

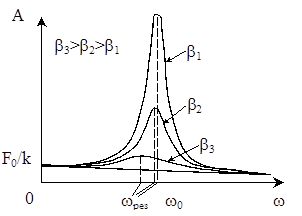
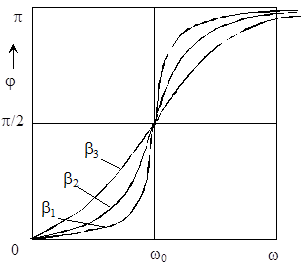
Рис. 6. Резонансные кривые Рис. 7. Зависимость j от w

 

Помимо рассмотренных выше типов колебаний существуют еще два вида колебательных процессов - параметрические колебания и автоколебания. Однако здесь они описываться не будут.

 

Контрольные вопросы.

1. Что такое колебания? Приведите примеры колебательных процессов.

2. Что называется периодом и частотой колебаний? Какова связь между периодом Т и частотами n и w?

3. Что такое гармонические колебания?

4. Запишите дифференциальные уравнения для свободных незатухающих и свободных затухающих колебаний, а также их решения.

5. Чем определяется собственная частота колебательной системы: а) при отсутствии затухания (b = 0); б) при наличии затухания (b ¹ 0).

6. Дать определение: декремента затухания, логарифмического декремента затухания, добротности и времени релаксации.

7. Что такое амплитуда и фаза колебаний?

8. Какова связь между амплитудой колебаний и энергией колеблющейся системы?

9. Запишите выражение для амплитуды затухающих колебаний. На что расходуется энергия, первоначально переданная системе?

10. Что такое вынужденные колебания? Запишите дифференциальное уравнение вынужденных колебаний. Каково его решение?

11. Поясните суть метода векторных диаграмм.

12. С помощью метода векторных диаграмм определите амплитуду вынужденных колебаний и сдвиг фаз между внешним воздействием и установившимися вынужденными колебаниями.

13. Что такое резонанс? Как выглядят резонансные кривые при различных коэффициентах затухания?

14. За счет чего возрастает амплитуда при резонансе? Почему с увеличением затухания значения резонансной амплитуды уменьшаются?

 

Электромагнитные колебания

 

Свободные незатухающие колебания в L-C контуре

Простейшей системой, в которой возникают электромагнитные колебания, является электрическая цепь, состоящяя из конденсатора С и катушки индуктивности L (L-С контур) - рис. 8.

 

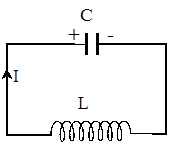
Рис. 8.

 

Если пренебречь активным сопротивлением (R = 0), то в L-C контуре возникают свободные незатухающие колебания.

Рассмотрим, как в такой системе возникает колебательный процесс.

Для наглядности удобно воспользоваться аналогией с какой-либо механической системой, например пружинным маятником. Напомним, что для возникновения свободных незатухающих колебаний необходимо, чтобы после выведения из положения равновесия (т.е. передачи энергии извне) в системе возникала возвращающая упругая или квазиупругая сила, а силы трения в ней либо малы, либо вовсе отсутствуют.

Передадим энергию в L-C контур, зарядив конденсатор:

W = CU²/2 = q²/2C. (19)

После подключения к заряженному конденсатору катушки индуктивности, он начнет разряжаться и в цепи появится ток I. Условимся считать положительным ток, заряжающий конденсатор. На рис.8 показана фаза перезарядки конденсатора. В отсутствие активного сопротивления (R = 0), закон Ома (IR = j₁ - j₂ + e₁₂) для такой цепи можно записать как

0 = - q/C - L(dI/dt), (20)

где разность потенциалов на обкладках конденсатора U = j₁ - j₂ = - q/C,

а ЭДС – есть ЭДС самоиндукции e_s = - L(dI/dt).

Учитывая, что I = dq/dt, ур-е (20), преобразуем к виду

d²q/dt² + w₀²q = 0, (21)

где w₀² = 1/ LC.

Видно, что ур.(21) аналогично ур.2а, т.е. соответствует незатухающим гармоническим колебаниям заряда:

q = q₀ cos (w₀t + a). (22)

В (22) и далее амплитудные значения будут обозначаться как q₀, U₀ и т.д.

Собственная частота контура: w₀ = 1/ .

Соответствующее выражение для периода колебаний называется формулой Томсона:

T= 2p . (23)

Напряжение (разность потенциалов) на конденсаторе и ток через катушку индуктивности:

U = q/С = U₀ cos (w₀t + a), (24)

U₀ =q ₀ /C,

I = dq/dt = - w₀ q₀ sin(w₀t + a) = I₀ cos (w₀t + a + p/2), (25)

I₀ = w₀q₀.

Видно, что сила тока по фазе опережает напряжение на конденсаторе. Следовательно, в момент времени, когда заряд (напряжение) на конденсаторе достигает максимальной величины, сила тока равна нулю и наоборот.

Таким образом, в L-C контуре возникают гармонические колебания заряда конденсатора и разности потенциалов (напряжения) на его обкладках, а также силы тока, текущего через катушку индуктивности. Одновременно с этим периодически (с частотой вдвое большей, чем для колебаний q и I) изменяется энергия электрического поля, запасенная в конденсаторе (q² /2C), и энергия магнитного поля, созданного током, текущим через катушку индуктивности (LI²/2).

Известно, что превращение энергии из одной формы в другую происходит при совершении работы. В данном случае эта работа есть:

DA = qe_s (26)

и совершается силами вихревого электрического поля. При разрядке конденсатора (q²/2C ® LI²/2) эта работа отрицательна (против э.д.с. самоиндукции e_s), а при его зарядке (LI²/2 ® q²/2C) положительна.

В механической колебательной системе взаимное превращение кинетической энергии в потенциальную и обратно происходит за счет работы упругой (квазиупругой) силы; знак работы зависит от направления процесса. Таким образом, напряженность вихревого электрического поля Е в известной степени является аналогом упругой силы в механических системах. Сопоставив колебания в L-C контуре с колебаниями пружинного маятника, можно провести и другие аналогии:

Маятник L-C контур

 

Потенциальная энергия

W_пот = kX²/2 W = q²/2C

 

Кинетическая энергия

W_кин = mv² /2 = (m/2)(dx/dt)² W = LI²/2 = (L/2) (dq/dt)²