Содержание
| Задача №1 | |
| Задача №2 | |
| Задача №3 | |
| Задача №4 | |
| Список литературы |
Задача №1
В процессе изменения состояния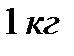 
газа внутренняя энергия его увеличивается на 
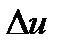. При этом над газом совершается работа, равная 
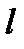. Начальная температура газа 
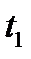, конечное давление 
.
Определить для заданного газа показатель политропы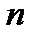 
, начальные и конечные параметры, изменение энтропии 
и изменение энтальпии 
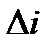
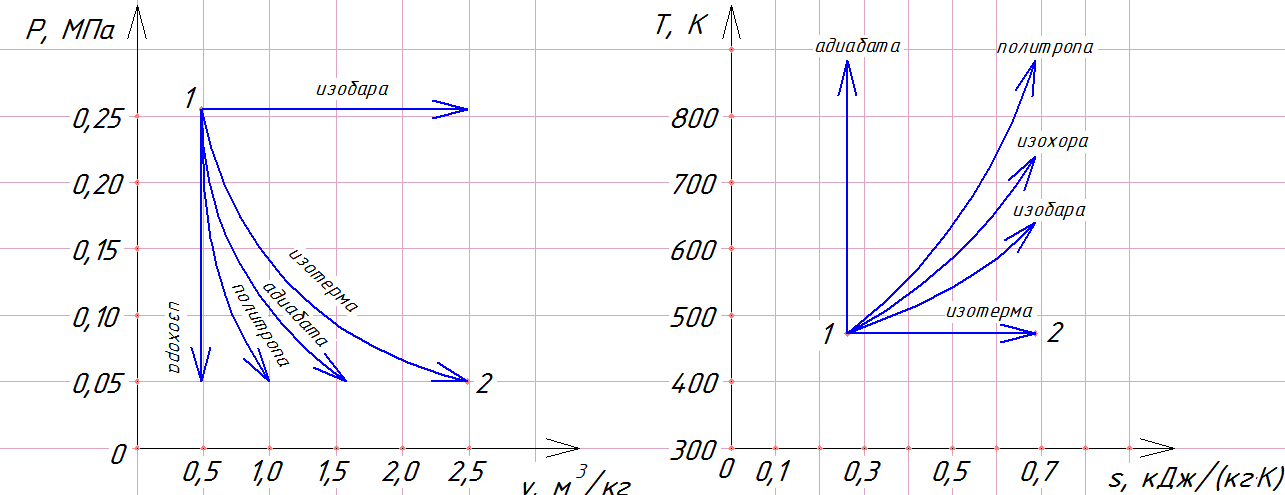
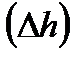. Представить процесс в 
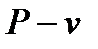и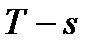 
координатах. Изобразить здесь же (без расчета) изобарный, изохорный, изотермический и адиабатный процессы, проходящие через начальную точку.
Решение:
1 Конечная температура процесса определяется из выражения для изменения внутренней энергии,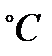 
:
,
где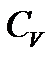 
– удельная массовая теплоемкость в процессе постоянного объема 
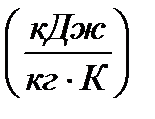, вычисляемая из соотношения:
.
Конечная температура процесса равна:
.
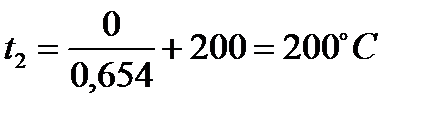2 Показатель политропы определяется из выражения для работы процесса:
,
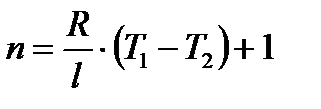где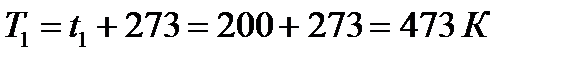 
;
;
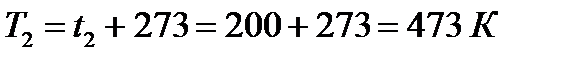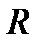– постоянная газовая постоянная, 
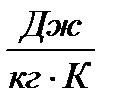, определяемая выражением:
,
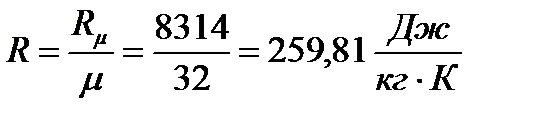где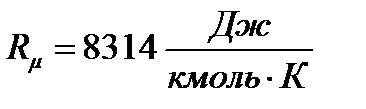 
– универсальная газовая постоянная.
Показатель политропы равен:
.
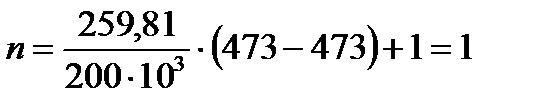Так как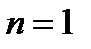 
, то процесс изотермический.
3 Начальное давление газа можно найти из соотношения параметров изотермического процесса,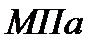 
:
;
.
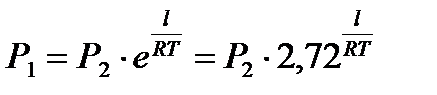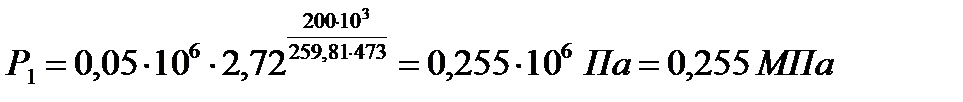4 Начальный и конечный объем определяем из характеристического уравнения состояния газа,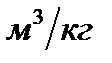 
:
;
.
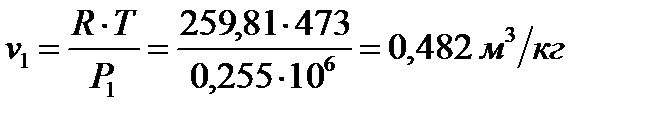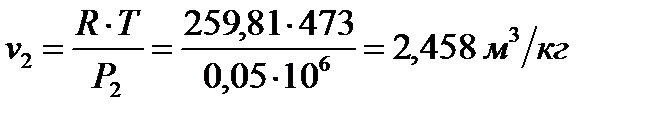5 Изменение энтропии составит,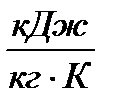 
:
.
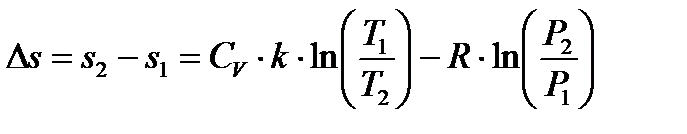Или для изотермического процесса:
.
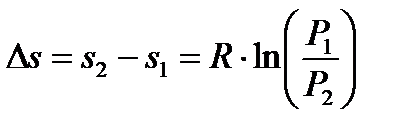
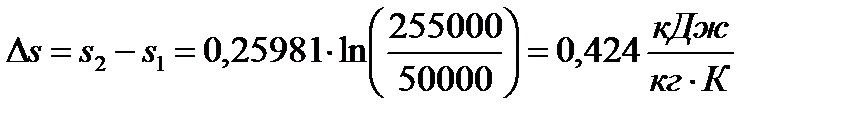6 Изменение энтальпии процесса,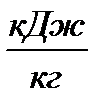 
:
.
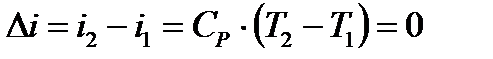7 Для построения процессов в координатах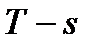 
необходимо вычислить значение энтропии газа в начальном состоянии по формуле, :
,
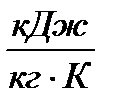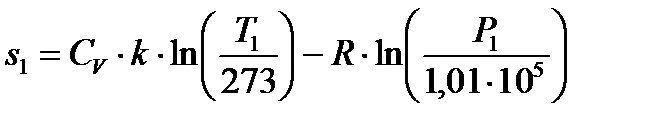где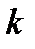 
– показатель адиабаты, определяемый зависимостью:
|
|
.
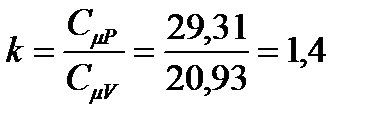Значение энтропии газа в начальном состоянии равно:
.
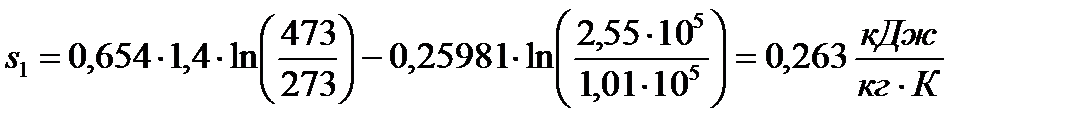8 Изображение термодинамических процессов.
Задача №2
Определить параметры рабочего тела в характерных точках идеального цикла поршневого двигателя внутреннего сгорания, если известны давление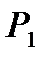 
и температура 
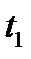рабочего тела в начале сжатия.
Степень сжатия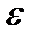 
, степень повышения давления 
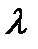, степень предварительного расширения 
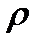заданы.
Определить работу, получаемую от цикла, его термический КПД и изменение энтропии отдельных процессов цикла.
За рабочее тело принять воздух, считая теплоемкость его в рабочих интервалах температур постоянной, построить в масштабе этот цикл в координатах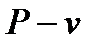 
и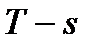 
.
Исходные данные и искомые показатели
| Дано | Определить | |
|  ,  ,  ,  , 
| 
|
|  ,  ,  , 
| 
|
|  ,  ,  , 
| 
|
| 
| 
|
| 
| 
|
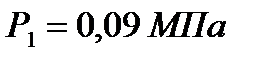
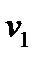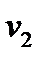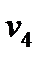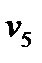
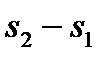
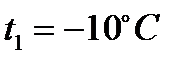
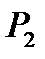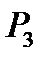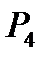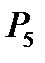
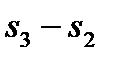
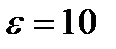
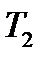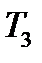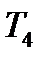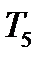
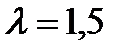
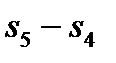
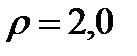
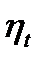
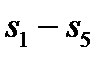
Решение:
1 Удельный объем воздуха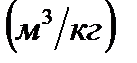 
в точке 1 цикла, соответствующей начальному состоянию, находится из характеристического уравнения:
,
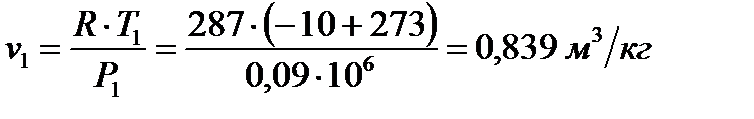где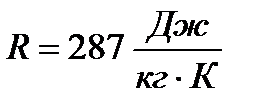 
– индивидуальная газовая постоянная воздуха.
2 Так как сжатие происходит по адиабатному процессу, то параметры состояния рабочего тела в точке 2 цикла определяются выражениями:
;
,
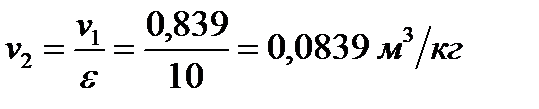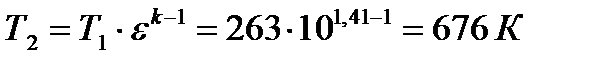где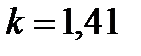 
– показатель адиабаты для воздуха.
.
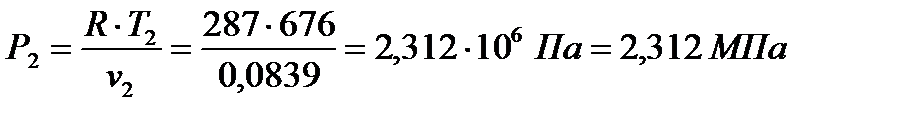3 В процессе 2-3 цикла осуществляется изохорный подвод теплоты в количестве 
. Исходя из этого, параметры рабочего тела в точке 3 будут иметь следующие значения:
;
;
.
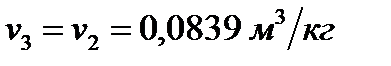4 Линия 3-4 на диаграмме изображает изобарный процесс подвода теплоты в количестве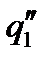 
. Исходя из условий изобарного процесса, параметры рабочего тела в точке 4 составят:
;
;
.
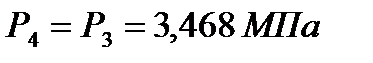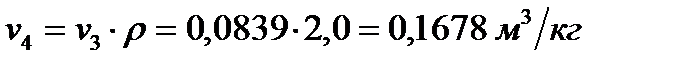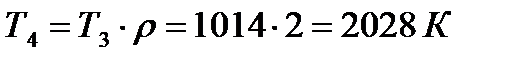5 Дальнейший процесс расширения происходит по адиабате 4-5. Параметры состояния рабочего тела в точке 5 определяются выражениями:
|
|
;
;
.
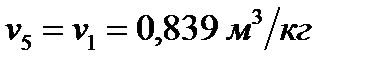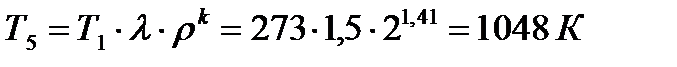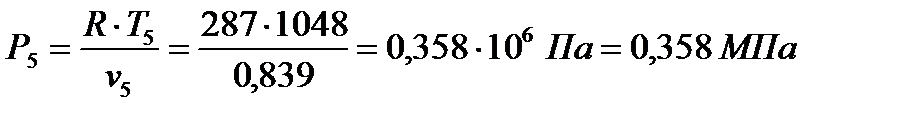6 Количество подведенной теплоты в цикле составит:
,
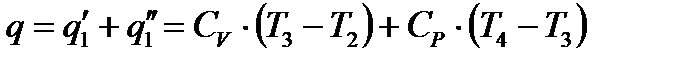где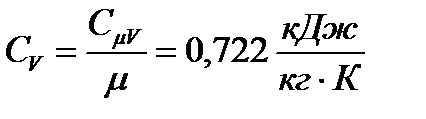 
– удельная массовая теплоемкость воздуха в процессе постоянного объема;
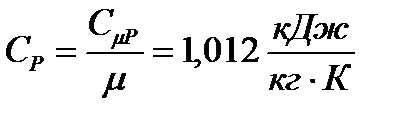– удельная массовая теплоемкость воздуха в процессе постоянного давления.
.
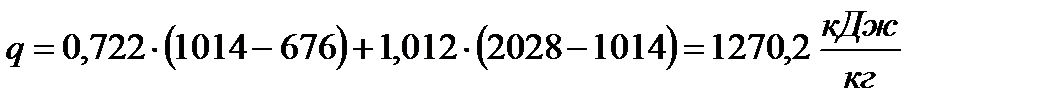7 Отведенная теплота цикла (процесс 5-1) равна:
.
8 Полезная работа цикла составит:
.
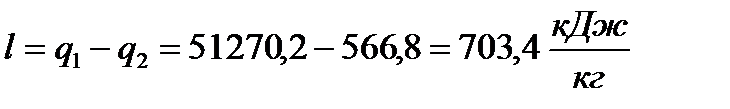9 Термический КПД цикла равен
.
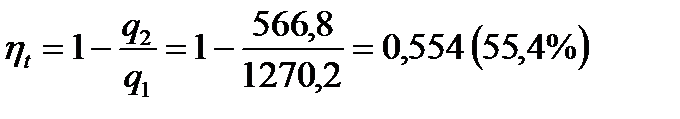10 Изменение энтропии в процессах цикла определяется по формуле:
.
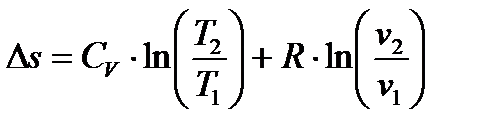Адиабатные процессы 1-2 и 4-5:
.
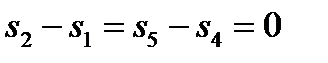Изохорный процесс 2-3:
.
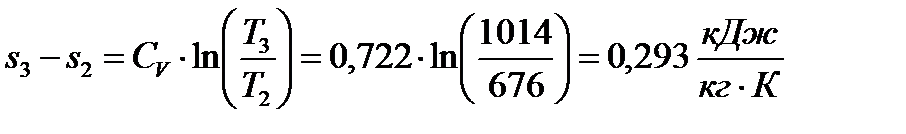Изобарный процесс 3-4:
.
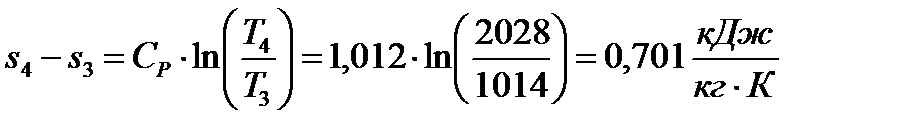Изохорный процесс 5-1:
.
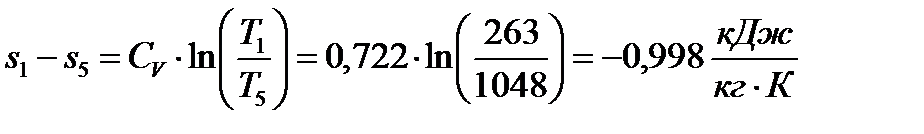Проверка.
Для цикла должно быть:
,
где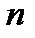 
– число участков цикла.
;
.
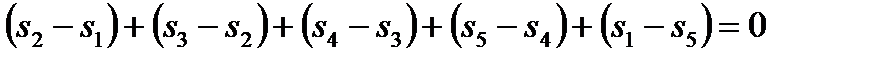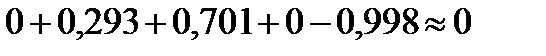Следовательно, вычисления выполнены правильно.
12 Для построения цикла в координатах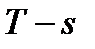 
необходимо вычислить значение энтропии газа в начальном состоянии по формуле:
;
.
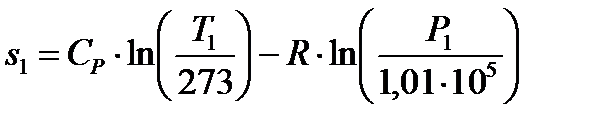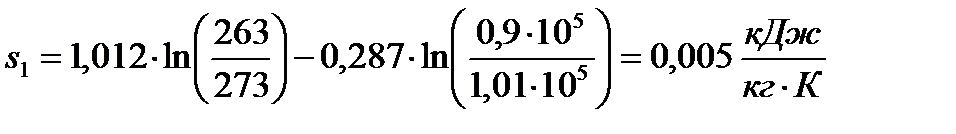13 Расчетные данные для построения цикла ДВС.
| Параметр | Координаты характерных точек цикла | |||||
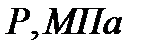
| 0,09 | 2,312 | 3,468 | 3,468 | 0,358 | |
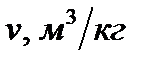
| 0,839 | 0,0839 | 0,0839 | 0,1678 | 0,839 | |
| ||||||
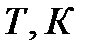
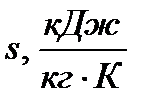
| 0,005 | 0,005 | 0,298 | 0,999 | 0,999 | |
14 Расчетная диаграмма термодинамического цикла ДВС со смешанным подводом теплоты (цикл Тринклера).
1-2 – сжатие;
2-3 – подвод теплоты в процессе расширения при постоянном давлении;
4-5 – расширение;
5-1 – выпуск ОГ при постоянном объеме.
15 Основные формулировки второго закона термодинамики.
¾ Теплота не может самопроизвольно переходить от более холодного тела к более нагретому (формулировка Клаузиуса).
|
|
¾ Вечный двигатель второго рода невозможен (формулировка Оствальда).
¾ Там где есть разница температур возможно совершение работы (формулировка Карно).
¾ Все самопроизвольные процессы в природе идут с увеличением энтропии.
¾ При прохождении в изолированной системе самопроизвольных процессов энтропия системы возрастает (энтропия изолированной системы стремится к максимуму, так как самопроизвольные процессы передачи тепла всегда будут происходить, пока есть перепады температур).
Задача №3
Показать сравнительным расчетом целесообразность применения пара высоких начальных параметров и низкого конечного давления на примере паросиловой установки, работающей по циклу Ренкина, определив располагаемый теплоперепад, термический КПД цикла и удельный расход пара для двух различных значений начальных и конечных параметров пара. Указать конечное значение степени сухости 
(при давлении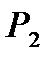 
).
Решение:
1 Термический КПД цикла Ренкина выражается формулой:
,
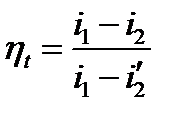где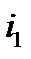 
– энтальпия перегретого пара, 
;
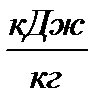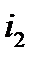– энтальпия пара в конце расширения, 
;
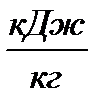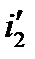– энтальпия конденсата 
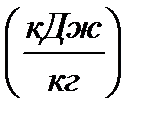, определяется выражением:
,
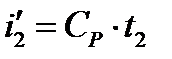где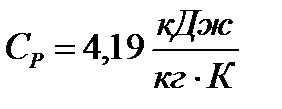 
– теплоемкость конденсата;
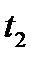– температура конденсата при давлении .
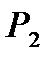2 Величину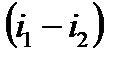 
называют располагаемым теплоперепадом, за счет которого производится полезная работа в цикле Ренкина. Величина 
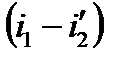отражает количество теплоты, затраченной в цикле.
Для определения значения энтальпии 
, находим на диаграмме 
водяного пара изобару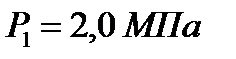 
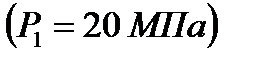и изотерму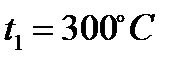 
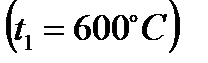. Пересечение этих линий образует точку 1, которая соответствует состоянию перегретого пара. По этой точке на оси ординат определяем величину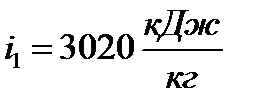 
.
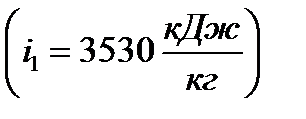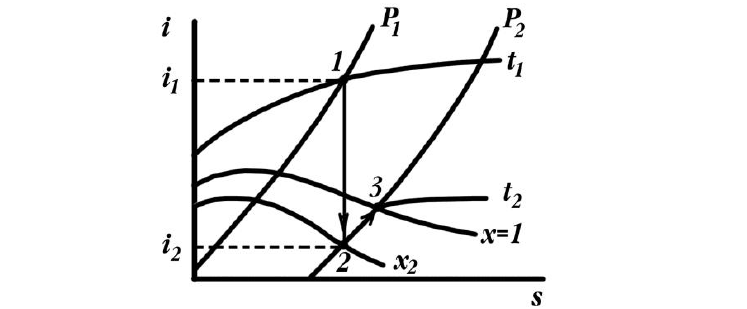
3 Так как в цикле Ренкина процесс расширения пара осуществляется по адиабате (изоэнтропийно), то на диаграмме он изображается вертикальной линией 1-2. В свою очередь, при пересечении адиабаты расширения, проведенной из точки 1, с изобарой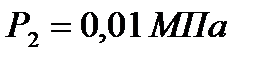 
получаем точку 2, соответствующую состоянию пара в конце расширения. По этой точке на оси ординат определяем величину энтальпии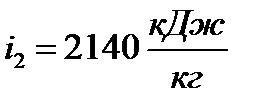 
.
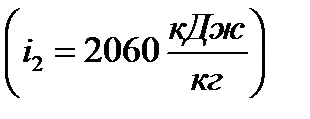4 После этого отработавший пар конденсируется при неизменном давлении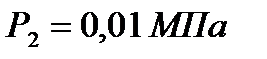 
и соответствующей этому давлению температуре 
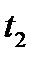. Так как в области влажного насыщенного пара изотермы и изобары совпадают, то для определения температуры отработанного пара из точки 2 диаграммы движемся по изобаре до пограничной линии 
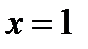. При степени сухости 
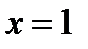(точка 3) изотерма отклоняется вправо от изобары. Эта изотерма соответствует значению 
.
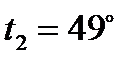Линия постоянной степени сухости, проходящая через точку 2, соответствует величине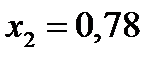 
.
По заданным значениям параметров из диаграммы следует:
| I вариант | II вариант |
| 
|
|
| 
|
|
|
| 
|
| 
|
| 
|
| 
|
| 
|
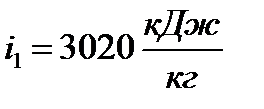
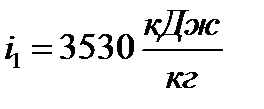
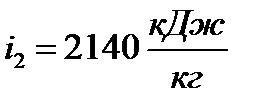
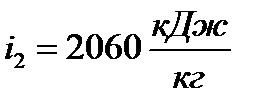
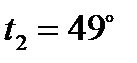
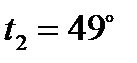
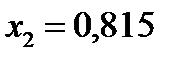
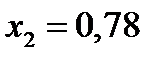
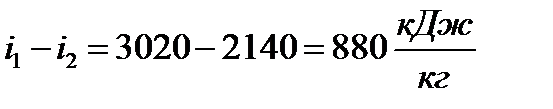
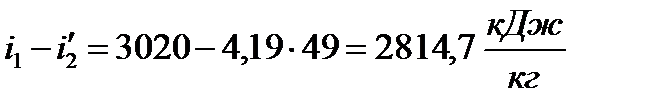
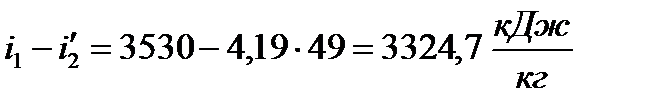
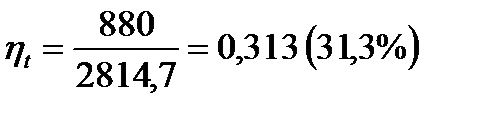
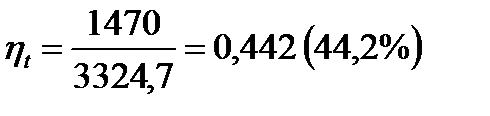
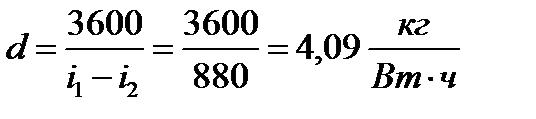
5 Схема графического решения задачи по диаграмме водяного пара.
6 Схема простейшей паросиловой установки.
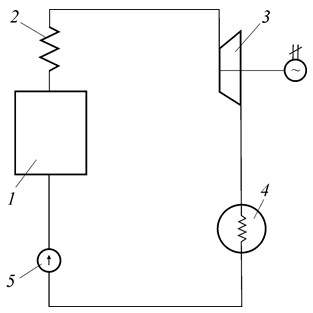
Краткое описание паросиловой установки:
В паровом котле паросиловой установки 1 за счет подвода теплоты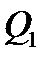 
, получаемой за счет сгорания топлива в топке, образуется пар при постоянном давлении 
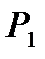. В пароперегревателе 2 он дополнительно нагревается и переходит в состояние перегретого пара. Из пароперегревателя пар поступает в паровой двигатель 3 (например, в паровую турбину), где полностью или частично расширяется до давления 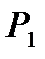с получением полезной работы 
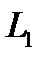. Отработанный пар направляется в холодильник-конденсатор 4, где он полностью или частично конденсируется при постоянном давлении 
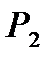. Конденсация пара происходит в результате теплообмена между отработавшим паром и охлаждающей жидкостью, протекающей через холодильник-конденсатор 4.
После холодильника сконденсированный пар поступает на вход насоса 5, в котором давление жидкости повышается с величины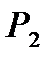 
до первоначального значения 
после чего жидкость поступает в паровой котел 1. Цикл установки замыкается. Если в холодильнике 4 происходит частичная конденсация отработавшего пара, то в паросиловой установке вместо насоса 5 используется компрессор, где давление пароводяной смеси также повышается с 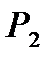до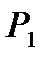 
. Однако для того, чтобы уменьшить работу на сжатие, целесообразно полностью сконденсировать пар в конденсаторе и затем сжимать не пароводяную смесь, а выходящую из конденсатора воду. Описанный цикл паросиловой установки называется циклом Ренкина.
7 Цикл Ренкина в координатах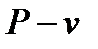 
и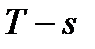 
.
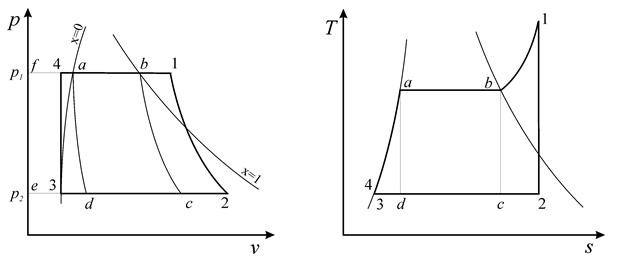
Цикл Ренкина состоит из изобары (4-1), где подводится теплота в нагревателе, адиабаты (1-2) расширения пара в паровой турбине, изобары (2-3) отвода теплоты в холодильнике-конденсаторе и изохоры (3-4) повышения давления воды в насосе. Линия (4-а) на изобаре соответствует процессу повышения температуры жидкости после насоса до температуры кипения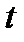 
при давлении . Участок (a-b) соответствует превращению кипящей жидкости в сухой насыщенный пар, а участок (b-1) – процессу подвода теплоты в пароперегревателе для превращения сухого насыщенного пара в перегретый.
Задача №4
Определить площадь поверхности нагрева газоводяного рекуперативного теплообменника, работающего по противоточной системе. Греющий теплоноситель – дымовые газ с начальной температурой 
и конечной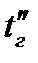 
. Расход воды через тепломобменник 
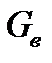, начальная температура воды 
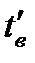, конечная 
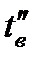. Коэффициент теплоотдачи от газов к стенке трубы 
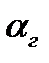и от стенки трубы к воде 
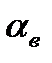. Теплообменник выполнен из стальных труб с наружным диаметром 
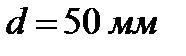и толщиной стенки 
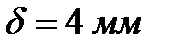. Коэффициент теплопроводности стали 
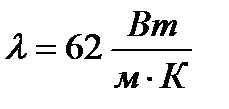. Стенку считать чистой с обеих сторон..
Определить также площадь поверхности теплообмена при выполнении теплообменника по прямоточной системе и сохранении остальных параметров неизменными.
Для обеих схем движения теплоносителей (противоточной и прямоточной) показать (без расчета) графики изменения температур теплоносителей вдоль поверхности теплообмена. Указать преимущества противоточной системы.
Решение:
1 Учитывая, что по условиям задачи отношение наружного диаметра к внутреннему меньше двух, расчет можно вести по формулам теплопередачи для плоской стенки в стационарном режиме, т.е.:
,
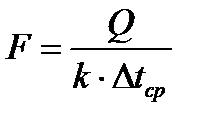где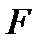 
– площадь поверхности теплообмена, исходя из среднего диаметра трубы, 
;
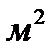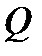– тепловой поток, 
;
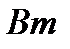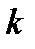– коэффициент теплопередачи, 
;
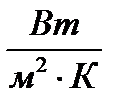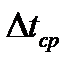– средний температурный перепад между теплоносителями (средний температурный напор),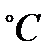 
2 Тепловой поток определяется выражением:
,
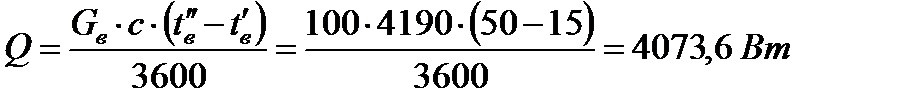где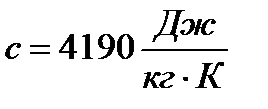 
– теплоемкость воды.
3 Коэффициент теплопередачи составит:
.
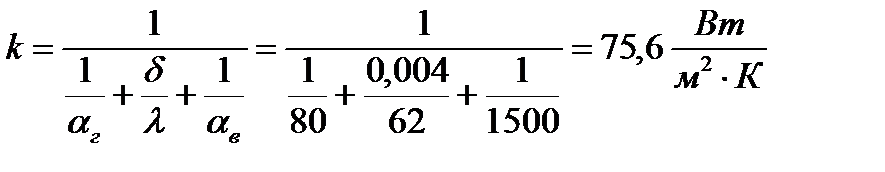4 Средний температурный напор определится исходя из схемы противоточного движения теплоносителей:
,
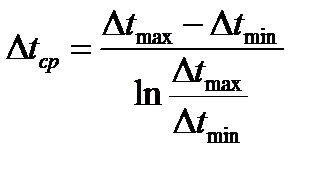где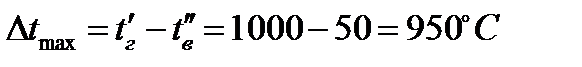 
;
.
.
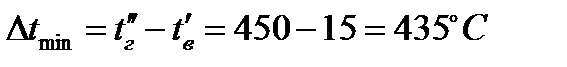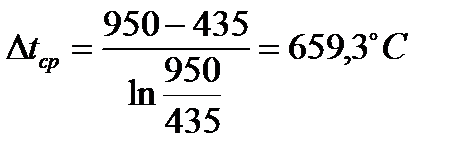5 Площадь поверхности теплообмена составит:
.
6 В случае применения прямоточной схемы теплообменного аппарата средний температурный напор составит:
,
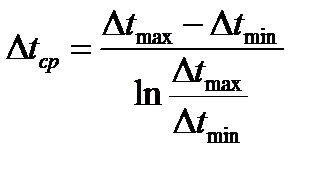где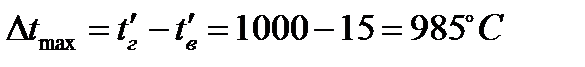 
;
.
.
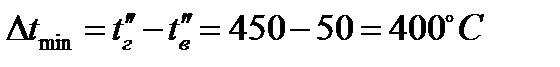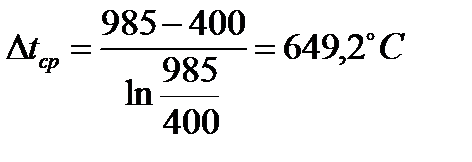Площадь поверхности теплообмена в данном случае составит:
.
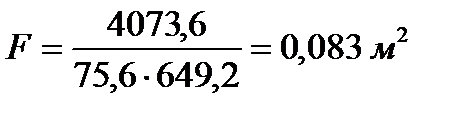7 Графики изменения температур теплоносителей вдоль поверхности теплообмена в прямоточном и противоточном теплообменных аппаратах.
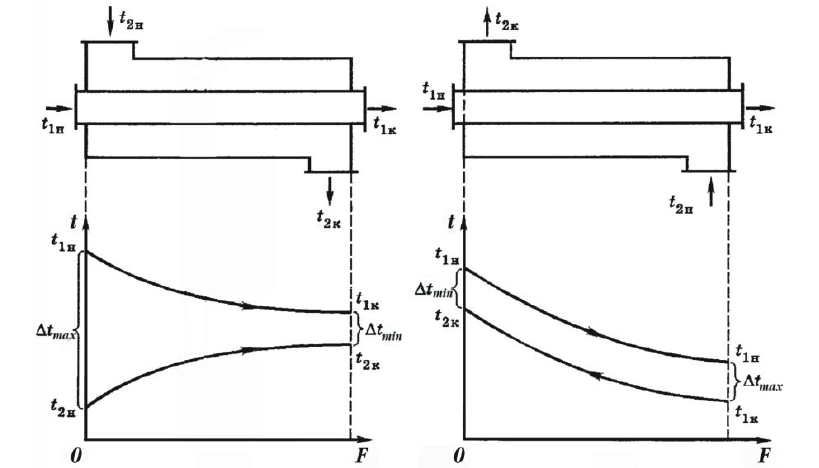
При равных условиях при противотоке передается больший тепловой поток, поэтому с данной точки зрения данная схема является более предпочтительной.
8 Коэффициент теплоотдачи 
характеризует процесс передачи тепла от некоторого теплоносителя (жидкость или газ) к твердой стенке. Определяется параметрами данного теплоносителя (режим течения, скорость, теплофизические характеристики типа – плотность, вязкость, теплопроводность), а также характеристиками той части стенки, которая омывается данным теплоносителем (характерный размер, наличие оребрения и т.п.)
Коэффициент теплопередачи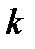 
характеризует процесс передачи тепла между двумя теплоносителями через разделяющую их твердую стенку. Определяется коэффициентами теплоотдачи обоих теплоносителей и параметрами теплопередающей стенки (толщина, теплопроводность).
Список литературы
1 Авчухов В.В., Паюсте Б.Я. Задачник по процессам тепломассообмена. Учеб. пособие для вузов. – М.: Энергоатомиздат, 1896. – 144 с. ил.
2 Кудинов В.А., Карташов Э.М. Техническая термодинамика. Учеб. пособие для вузов. М.: Высш. шк., 2000. – 261 с., ил.
3 Панкратов Г.П. Сборник задач по теплотехнике: Учеб. пособие для неэнергетич. спец. Вузов. – 2-е изд., перераб. и доп. – М.: Высш. шк. 1986. – 248 с., ил.
4 Рабинович О.М. Сборник задач по технической термодинамике. М.: «Машиностроение», 1973. – 344 с.
5 Телегин, А. С. Теплотехника и нагревательные устройства / А.С. Телегин, В. Г. Авдеева. - М.: Машиностроение, 1985. - 248 с.
6 Щербинин В.В. Теплотехника: учебно-методическое пособие. / В.В. Щербинин, В.В. Павленко. Барнаул: Изд-во АГАУ, 2007. 40 с.