II. ТЕПЛОВОЙ РАСЧЕТ РАДИАТОРА ДВС.

Исходные данные для расчетов.

Таблица 4.

Исходные данные

Наименование показателя	Обозначение показателя	Единица измерения показателя	Численное значение показателя
Мощность теплового потока, отводимого от ДВС в охлаждающую жидкость	Q	кВт
Объемный расход воздуха через радиатор	G02		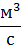1,9
Размер радиатора по глубине	a	м	0,1
Размер радиатора по ширине	b	м	0,4
Длина радиаторных трубок	lр	м	0,4
Коэффициент оребрения	ψ	-	8,5
Толщина стенок трубок радиатора	δ	м	0,1∙10-3
КПД радиатора	ηр	-	0,97
Средняя температура охлаждающей жидкости	t1ср	°С
Плотность охлаждающей жидкости	ρ1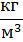
Удельная теплоемкость охлаждающей жидкости при постоянном давлении	cp1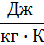
Коэффициент теплопроводности охлаждающей жидкости	λ1		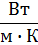0,666
Коэффициент кинематической вязкости охлаждающей жидкости	ν1		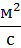0,39∙10-6
Температурный коэффициент объемного расширения охлаждающей жидкости	βт1	К-1	6,02∙10-4
Средняя температура воздуха в радиаторе	t2ср	°С
Плотность воздуха	ρ2		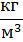1,21
Удельная теплоемкость при постоянном давлении воздуха	cp2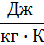
Коэффициент теплопроводности воздуха	λ2		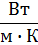2,59∙10-2
Коэффициент кинематической вязкости воздуха	ν2		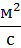15∙10-6
Температура охлаждающей жидкости на входе в радиатор	t1`	°С
Температура охлаждающей жидкости на выходе из радиатора	t1``	°С
Температура воздуха на входе в радиатор	t2`	°С
Коэффициент теплопроводности алюминия (материал - алюминий)	λм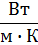

 

Тепловой расчет радиатора с числом трубок равным десяти (n = 10).

1) Определяем величину массового расхода воздуха:

(),

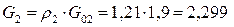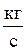где ρ₂ - плотность воздуха, ;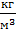

G₀₂ - объемный расход воздуха через радиатор, .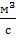

2) Определяем температуру воздуха на выходе из радиатора, принимая мощность теплового потока, полученной при охлаждении горячего теплоносителя Q₁ равной заданной величине мощности теплового потока, отводимого от ДВС в охлаждающую жидкость Q:

 

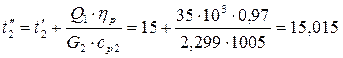(°С),

 

где t₂` - температура воздуха на входе в радиатор, °С;

η_р - КПД радиатора;

c_p2 - удельная теплоемкость при постоянном давлении воздуха, .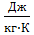

 

3) Определяем мощность теплового потока, полученную тепловым носителем:

 

 

Из уравнения теплового баланса для системы охлаждения:

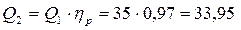(кВт).

 

 

Из уравнения теплопередачи:

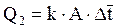, кВт.

 

где k – коэффициент теплопередачи;

А – площадь поверхности теплообмена;

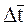– среднелогарифмический температурный напор.

 

4) Определяем режим течения воды внутри трубок радиатора.

Критерием служит значение критического числа Рейнольдса Re_кр = 2300. Значение числа Рейнольдса (рассчитанное в разделе I) Re = Re₁ = 100386,67.

Так как Re₁ = 100386,67 > Re_кр = 2300 режим течения воды внутри трубок радиатора будет турбулентным.

 

5) Для случая турбулентного течения воды внутри трубок радиатора значение критерия Нуссельта определяют по формуле:

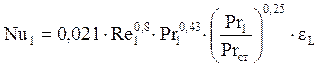
где ε_L – поправочный коэффициент, учитывающий влияние начального участка, так как 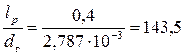> 50, то ε_L = 1;

l_р - длина радиаторных трубок, м;

Re₁ - критерий Рейнольдса для охлаждающей жидкости;

Pr₁ - критерий Прандтля для охлаждающей жидкости;

Pr_ст - критерий Прандтля для стенок трубок радиатора;

 

 

6) За определяющую температуру, при которой определяются теплофизические параметры теплоносителя, принята средняя температура воды:

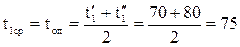(°С),

 

где t₁` – температура охлаждающей жидкости на входе в радиатор, °С;

t₁`` – температура охлаждающей жидкости на выходе из радиатора, °С.

 

7) Значение критерия Прандтля определяют при определяющей температуре, равной средней температуре стенок трубок:

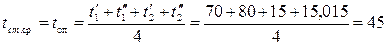(°С).

По справочнику определяем значение критерия Прандтля для стенок трубок радиатора:

Pr_ст = 7.

 

8) Определяем значение критерия Прандтля для охлаждающей жидкости:

 

,

 

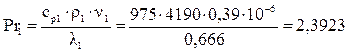где c_p1 - удельная теплоемкость охлаждающей жидкости при постоянном давлении, ;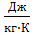

ρ₂ - плотность охлаждающей жидкости, ;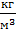

ν₁ - коэффициент кинематической вязкости охлаждающей жидкости, ;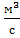

λ₁ - коэффициент теплопроводности охлаждающей жидкости, .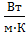

 

9) Определяем значение критерия Нуссельта для охлаждающей жидкости:

 

 

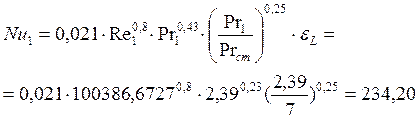
10) Определяем коэффициент теплоотдачи от воды к стенке трубок:

().

 

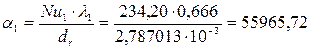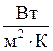11) Определяем критерий Нуссельта для случая поперечного обтекания пучка труб в радиаторе:

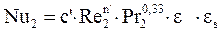
где Re₂ – критерий Рейнольдса для воздушного потока;

Pr₂ – критерий Прандтля для воздушного потока;

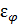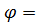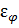– поправочный коэффициент, учитывающий угол между направлением течения потока и осью труб, следовательно при 90°С = 1;

ε_s – поправочный коэффициент, учитывающий влияние поперечного S₁ и продольного S₂ шагов;

с` и n` – коэффициенты, зависящие от взаимного расположения труб.

12) По рис. 2 «Поперечное сечение радиатора (n=10) определяем шаги:

 

S₁ = 70 мм = 0,070 м;

S₂ = 60 мм = 0,060 м.

Рисунки с трубками далее!!!!

 

 

Так как отношение шагов 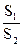> 2, то для шахматного расположения пучка труб ε_s = 1,12, если 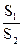< 2, то ε_s = 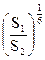; с`= 0,41 и n`= 0,6;

Для всех трубок (n=10,50,100,200,400) 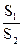< 2.

ε_s10 =1,03

ε_s50 =1,1

ε_s100 =0,98

ε_s200 =1,1

ε_s400 =0,98

13) Определяем площадь живого сечения по воздуху:

 

А_ж = l_р∙(b-n₁∙(d_г+2∙δ)),

 

где b – размер радиатора по ширине, м;

δ – толщина стенок трубок радиатора, м;

n₁ – количество трубок, расположенных во фронтовом сечении радиатора (см. рис. 2 «Поперечное сечение радиатора (n=10)»);

n₁ = 3 трубки во фронтовом сечении радиатора с числом трубок равным десяти.

 

А_ж = 0,4∙(0,4-5∙(2,787013∙10^-3+2∙0,1∙10^-3)) = 0,154 (м²).

 

14) Определяем фронтовую поверхность радиатора:

А_фр = b∙l_р = 0,4∙0,4 = 0,16 (м²).

 

15) Определяем коэффициент живого сечения:

.

 

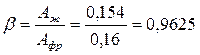16) Определяем скорость воздуха перед фронтом радиатора:

.

 

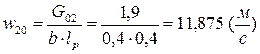17) Определяем критерий Рейнольдса для воздушного потока:

,

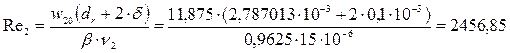где ν₂ – коэффициент кинематической вязкости воздуха, .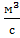

18) Критерий Прандтля для воздуха слабо зависит от температуры и в диапазоне значений температур 10 ÷ 30°С можно принять Pr₂ = 0,703.

 

19) Определяем критерий Нуссельта для случая поперечного обтекания пучка труб в радиаторе:

 

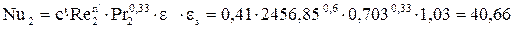
20) Определяем коэффициент теплоотдачи от оребренной поверхности трубок к воздуху:

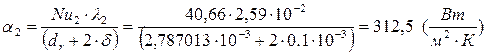
где λ₂ – коэффициент теплопроводности воздуха, .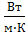

 

21) Определяем коэффициент теплопередачи:

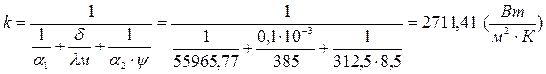
где λ_м – коэффициент теплопроводности алюминия (материал - алюминий), ;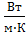

ψ – коэффициент оребрения.

 

22) Определяем среднелогарифмический напор:

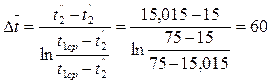(°С).

 

23) Определяем поверхность теплообмена:

 

А = π∙d_ср∙n∙l_р;

 

где d_ср = d_г + δ = 2,787013∙10^-3+0,1∙10^-3 = 2,887013∙10^-3 (м);

 

А = 3,14∙2,887013∙10^-3 ∙10∙0,4 = 36,26∙10^-3 (м²).

 

24) Из уравнения теплопередачи определяем мощность теплового потока, полученную тепловым носителем:

 

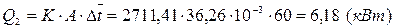
25) Тогда мощность теплового потока, полученной при охлаждении горячего теплоносителя, определяется по формуле:

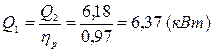
Расчет для радиатора с числом трубок равным пятидесяти, ста, двумстам, четыремстам (n = 50, 100, 200, 400) ведется аналогично тепловому расчету радиатора с числом трубок равным десяти (n = 10).

 

Итоговые данные приведены в таблице 5.

Таблица 5.

 

Полученные значения искомых величин при тепловом расчете радиатора ДВС с числом трубок равным 10, 50, 100, 200, 400

n, шт	dг∙10-3, м	S1, м	S2, м	α1,	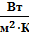α2,	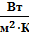k,	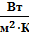Q1, кВт
	2,787013	0,070	0,060	55965,72	312,5	2711,41	6,37
	1,510141	0,035	0,020	46483,34	404,7	3464,6	25,87
	1,159928	0,018	0,020	42913,73	468,70	3756,2	35,68
	0,89089	0,018	0,010	39553,77	570,04	4216,5	66,74
	0,684438	0,009	0,010	36577,37	574,01	4475,5	103,32

Построение графиков зависимостей мощности теплового потока Q₁ и коэффициента теплопередачи k от гидравлического диаметра трубокd_г

 

 

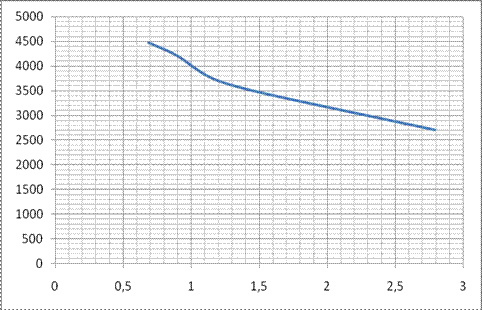
График 3. Зависимость коэффициента теплопередачи k от гидравлического диаметра трубокd_г.

По графику 4 «Зависимость мощности теплового потока Q₁ от гидравлического диаметра трубок d_г» определяем гидравлический диаметр трубок, а следовательно и количество трубок n (см. график 1 «Зависимость гидравлического диаметра трубок от их количества»), при котором обеспечивается отвод заданной мощности теплового потока Q от двигателя.

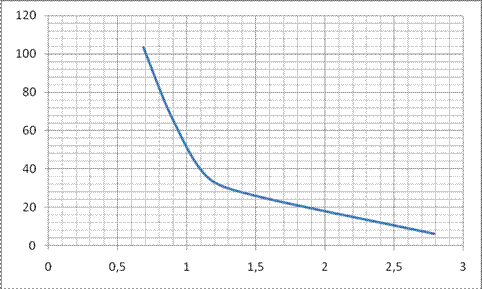
График 4. Зависимость мощности теплового потока Q₁ от гидравлического диаметра трубок d_г.

 

 

Таким образом, для отвода заданного теплового потока Q = 35 кВт от двигателя внутреннего сгорания требуется радиатор с гидравлическим диаметром трубок d_г = 1,12∙10^{-3 м и числом трубок} n = 124 шт.