Алгоритмы и схемы демодуляции

Модели и методы демодуляции сигналов с частотной манипуляцией

(реферат)

Варлакова Евгения
МГТУ, Морская Академия,

Судоводительский факультет,

Рт-4

Аннотация

Представлены модели сигналов с частотной манипуляцией (ЧМн-сигналов) и некоторые способы построения структур их демодуляторов. Проведен анализ ал­горитмов демодуляции ЧМНФ-сигналов (частотно-манипулированных с непре­рывной фазой) как с позиции рабочих характеристик в условиях малых соотноше­ний сигнал/шум, так и с позиции сложности и эффективности аппаратной реали­зации. Даются рекомендации по выбору схем демодуляции.

 

Введение

Несмотря на достаточно долгую историю, вопрос о грамотном выборе структуры и параметров цифрового демодулятора ЧМн-сигналов далек от окончательного решения.

Главные проблемы, связанные с демодуляцией ча-стотно-манипулированных сигналов с непрерывной фазой (ЧМНФ-сигналов) в условиях малых отноше­ний сигнал/шум, обусловлены сглаживанием фазо­вых переходов при модуляции, благодаря чему до­стигается высокая эффективность использования канала передачи.

Вследствие выраженных корреляционных свойств между реализациями при символьных переходах ЧМНФ-сигналов классические алгоритмы демодуля­ции, основанные на оптимальной фильтрации и ис­пользующие свойство ортогональности процессов, соответствующих различным информационным сим­волам, в данном случае теряют эффективность, осо­бенно при малых отношениях сигнал/шум. Указанные обстоятельства обусловливают применение специально разработанных для данных сигналов мето­дов демодуляции и символьной синхронизации.

При выборе алгоритмов основное внимание уделялось возможности аппаратной реа­лизации последних в условиях портативных мобиль­ных систем.

Модели и методы демодуляции сигналов с частотной манипуляцией

Свойства ЧМНФ-сигналов

Спектр частотно-манипулированного сигнала без сглаживания фазы с перестройкой частоты по скач­кообразному закону где - девиа­ция частоты, обладает повышенным уровнем боковых составляющих [2], и, следовательно, занимает отно­сительно большую полосу частот при передаче. Для подавления боковых полос с сужением спектра пере­даваемого ЧМн-сигнала необходимо использование одной непрерывно изменяющейся несущей частоты [4]:

(1)

где - исходный модулирующий процесс (после­довательность прямоугольных импульсов). Из (1) видно, что при разрывном сигнале результирую­щий сигнал, таким образом, имеет непрерывную фа­зу. Последняя для ЧМНФ-сигнала определяется в со­ответствии с выражением [2]:

(2)

где 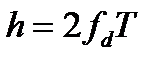- индекс модуляции; - максимальная девиация частоты; 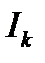- последовательность информа­ционных символов, для двоичных символов ; - канальный период передачи символа;

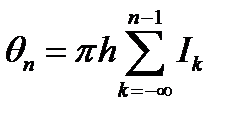- фаза накопленная от всех ранее посту­пивших информационных символов (кор­релированный вектор состояний);

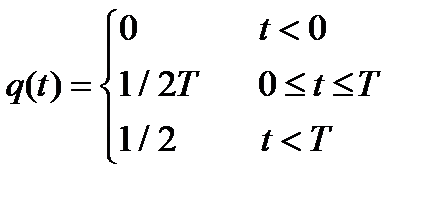
Из (2) можно заключить: ЧМНФ-сигнал обладает памятью, обусловленной непрерывностью фазы.

Таким образом, суммарная фаза сигнала предста­вляется как сумма фазовых компонент от п-1 предыду­щих принятых символов (коррелированного вектора состояний) и компонента, определяемого последним принятым символом. При приеме очередного двоично­го символа, как следует из (2), фаза ЧМНФ сигнала из­меняется на постоянную величину приращения:

(3)

Текущую фазу несущей можно представить в виде диаграммы фазовых траекторий, начинающихся с момента времени t=0 (рис. 1).

Рис. 1. Диаграмма фазовых траекторий бинарного ЧМНФ-сигнала

На диаграмме, представленной на рис. 1, стрелка­ми показаны фазовые траектории сигнала, формируемые в результате модуляции различными последо­вательностями . Восходящие векторы соответ­ствуют увеличению фазы, нисходящие - уменьше­нию. Так, на интервале [0;ЗТ] показаны все возмож­ные траектории изменения фазы из нулевого значе­ния до величин . Ширина фазовых тра­екторий (деревьев) увеличивается пропорционально времени, однако вследствие ограниченности фазы несущей интервалом (0,2п) последние переходят в решетчатую структуру (trellis) ограниченной ширины, число фазовых состояний в которой определяется индексом модуляции h. Так, например, при h=l/2 ре­шетка двоичной ЧМНФ обладает четырьмя фазовыми состояниями. Существует другая альтернативная форма представления фазовых траекторий - в виде графа состояний [2].

При индексе модуляции h=l/2 имеет место особый частный случай ЧМНФ-сигнала - модуляция с мини­мальным сдвигом фазы (ММС). На основании (1) и (2) сигнал в этом случае будет представляться как:

(4)

где nТ < t < (n + 1)T.

Из (4) следует, что ММС-сигнал s(t) является ЧМн-сигналом с постоянной огибающей и непрерывной фазой. Значения частоты: . Разность частот соответствует минималь­ному сдвигу, обеспечивающему ортогональность сиг­налов, соответствующих противоположным симво­лам, на интервале Т.

Таким образом [2], индекс модуляции h≥0,5 - для обеспечения ортогональности сигналов символов двоичного алфавита и, следовательно, наименьшей вероятности ошибки. Например, при скорости пере­дачи R=9,6 Кбит/с, девиация ≥2,4 КГц.

Описанные выше фазовые свойства памяти сигна­ла позволяют достичь значительного выигрыша в от­ношении сигнал/шум при демодуляции ЧМНФ-сигна­лов. Так как число фазовых состояний решетки неве­лико (на практике равно 4...8), то возможно выделе­ние наиболее правдоподобной фазовой траектории с определенной заранее фиксированной глубиной. Данная задача очень эффективно, с минимальными вычислительными затратами, решается путем при­менения алгоритма Витерби [6].

Спектральная плотность мощности бинарного ЧМНФ-сигнала определяется как [2]:

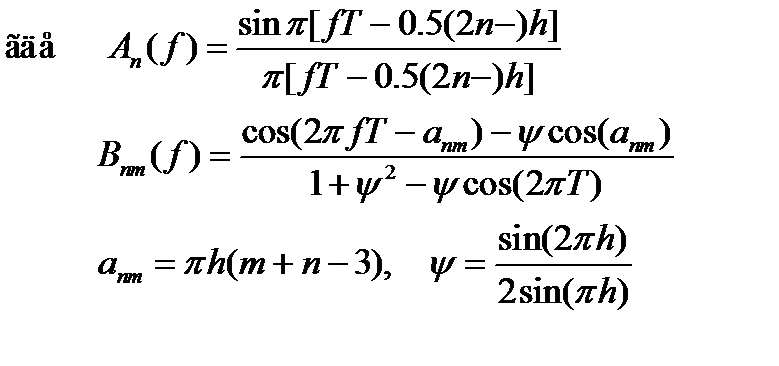
Из выражения для спектральной плотности можно сделать вывод, что уровень боковых лепестков и эффек­тивная ширина полосы спектра ЧМНФ-сигнала резко возрастают с увеличением индекса модуляции И. Наибо­лее узкую эффективную полосу занимают ММС-сигналы, которые, благодаря описанным свойствам, в настоя­щее время применяются в спутниковой связи, в военных системах связи и управления и т. п. [4]. Постоянство оги­бающей ММС-сигнала позволяет устранить паразитную амплитудную модуляцию (ПАМ), присущую сигналам с ЧМн с разрывом фазы.

Из рассмотрения свойств ЧМНФ-сигналов можно сделать следующие выводы:

1. Непрерывность фазы процесса с ЧМ приводит к по­давлению боковых составляющих спектра и более эф­фективному использованию канала; отсутствие резких фазовых скачков сигнала позволяет организовать коге­рентный прием последнего, дающий значительный вы­игрыш (до 3 дБ) в отношении сигнал/шум по сравнению с некогерентным.

2. Сигнал с непрерывной фазой обладает свойством памяти, которое заключается в однозначной зависимо­сти его фазовой траектории от последовательности пе­реданных символов; каждый символ вносит постоянный вклад в накапливаемую фазу, зависящий от индекса мо­дуляции.

3. Свойства ЧМНФ-сигнала, обусловленные практи­чески небольшим числом состояний решетки фазовых траекторий с постоянным шагом, позволяют восстана­вливать последние на приемном конце и при декодиро­вании использовать эффективные методы, основанные на вычислении наиболее правдоподобной последова­тельности передаваемых символов (алгоритм Витерби).

4. Число фазовых состояний и эффективная ширина спектра сигнала определяется индексом модуляции И. При h=0,5 (минимальном значении индекса модуляции, необходимом для ортогональности сигналов, соответ­ствующих символам алфавита) имеет место модуляция с минимальным сдвигом фазы.

Алгоритмы и схемы демодуляции

Достижение высокой спектральной эффективности ЧМНФ-сигналов об­условлено применением малых индексов модуляции h=0,5...1 совместно с непрерывностью фазы несущей частоты. Данные обстоятельства обусловливают применение специально разработанных для данных сигналов методов демодуляции. Классические алго­ритмы демодуляции ЧМ-сигналов, основанные на оп­тимальной фильтрации, базируются на ортогональ­ности сигналов, соответствующих различным инфор­мационным символам. При демодуляции ЧМНФ-сиг­налов в условиях малых отношений сигнал/шум по­следние теряют эффективность, что обусловлено по­терями ортогональности, вызванными выраженными корреляционными свойствами между реализациями при символьных переходах.

Большинство алгоритмов демодуляции последних основано на принципах классической теории оценок. Высокая эффективность данных алгоритмов достига­ется за счет реализации оценок межсимвольных фа­зовых переходов между двумя или более соседними символами, осуществимой с той или иной точно­стью. Однако, как показано ниже, при определенных допущениях возможно применение и некогерентных алгоритмов, обладающих более простой аппаратной реализацией.

Далее последовательно рассмотрим ряд алгорит­мов, применяемых для демодуляции ЧМНФ-сигналов.

Структурная схема некогерентного фильтрового обнаружителя приведена на рис.2.

Рис. 2. Структурная схема некогерентного фильтрового обнаружителя ЧМн-сигналов

 

Детектор состоит из отдельных каналов, каждый из которых включает полосовой фильтр и детектор, со­гласованный с формой огибающей сигнала, и схемы принятия решения. При выделении огибающей ин­формация о фазе сигнала теряется автоматически. При бинарной ЧМн решение о величине переданного символа принимается по максимальному выходному сигналу детектора на момент измерения.

Помехоустойчивость данного приема может быть оценена из следующих соображений. Предположим, что полоса узкополосного фильтра F_Э = n/T, n>1, Т-длительность информационного символа. Девиация частоты примерно соответствует значению F_Э. Пред­полагается также, что индекс модуляции m>1. При на­личии на входе полезного сигнала и помехи на выхо­де узкополосного фильтра случайный процесс ра­спределяется по Раису:

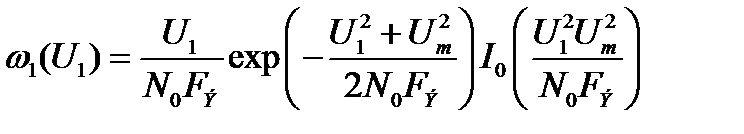
где I₀- модифицированная функция Бесселя нулево­го порядка.

Если на выходе присутствует только шум, то для этого случая характерно распределение Рэлея:

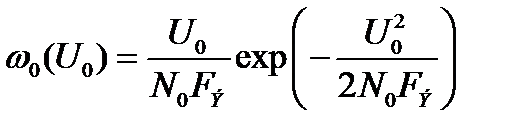
В формулах учтено, что дисперсия помехи равна - амплитуда сигнала на входе. При симметричном канале вероятность ошибки

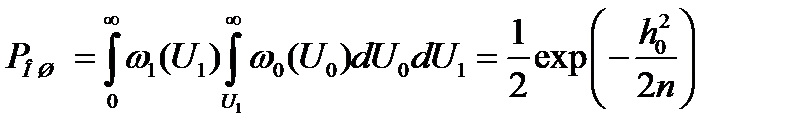
где 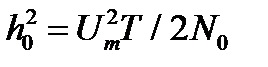отношение сигнал/помеха

Для ЧМн-сигналов с большими индексами модуля­ции (m>10) на выходе фильтра помехового канала можно пренебречь откликом и считать, что он опре­деляется только шумом. При этом оптимальным зна­чением полосы пропускания фильтров являются сле­дующие величины:

- для П-образного фильтра ( = 1,37/Т) отношение сигнал/шум ;

- для резонансного контура ( = 0,65/Т) отноше­ние сигнал/шум .

При этом вероятность ошибки рассчитывается по формуле:

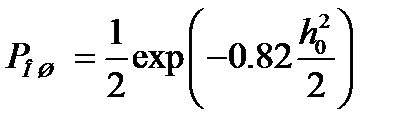
т.е. энергетический проигрыш приема по огибающей для широкополосной ЧМ по сравнению с оптималь­ным некогерентным приемом составляет примерно 1 дБ (18%).

При приеме ЧМ-сигналов с малым индексом моду­ляции (т= 0.5;1...) нельзя пренебрегать откликом на выходе фильтра помехового канала. Показано, что оптимальное значение полосы пропускания для приема по огибающей с учетом перекрытия спек­тров: одиночного контура ≈1,1T, П-образного фильтра ≈ 2Т. Формула вероятности ошибки в этом случае представляется в виде:

Таким образом, энергетический проигрыш метода приема по огибающей для узкополосной ЧМ по отно­шению к оптимальному некогерентному приему со­ставляет около 3 дБ, а по сравнению с когерентным - не менее 4 дБ.

Помимо указанных обстоятельств, алгоритм име­ет значительно более сложную аппаратную реализа­цию, обусловленную применением высокодобротных точных полосовых фильтров. В цифровом варианте вместо фильтров с высокой вероятностью потребует­ся применение схемы БПФ, что обусловлено высокой вычислительной сложностью.

Схема приема по мгновенной частоте состоит из ограничителя и дискриминатора. Напряжение на вы­ходе дискриминатора пропорционально мгновенной частоте суммы сигнала и помехи. Пусть частота нажа­тия , частота «отжатия» . Мгно­венная частота принятого сигнала равна сумме ча­стоты сигнала и производной по времени помехи . Ошибка при демодуляции произойдет, если производная помехи превысит девиацию часто­ты 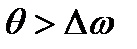. Если - плотность вероятности произ­водной помехи, то вероятность ошибки можно пред­ставить следующей формулой:

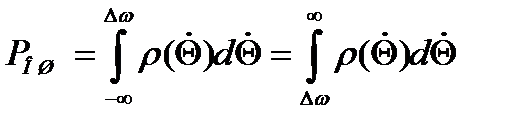
Выражения для распределения мгновенной часто­ты представим при помощи Q-функции. Для сим­метричного фильтра после интегрирования вероят­ность ошибки

где функция распределения Рэлея-Райса (Q-функция); - средний ква­драт частоты спектра шума на выходе фильтра:

где -аплитудно-частотная характеристика по­лосовых фильтров частотного детектора. В реальных схемах фильтров к моменту отсчета устанавливается стационарный режим, и сигнал практически не осла­бляется. Если при этом (это оптимальное зна­чение девиации при приеме частотной телеграфии по мгновенной частоте, а также учитывая, что эффек­тивная полоса пропускания фильтра в данном методе должна быть в 2 раза шире, чем полоса фильтра при приеме по огибающей), то вероятность ошибки прио­бретает простое выражение:

Таким образом, помехоустойчивость приема ЧМ сигналов в соответствии с методами приема по оги­бающей и по мгновенной частоте примерно одинако­вы и проигрывают в энергетике оптимальному неко­герентному приему не менее ЗдБ.

Рассмотрим когерентный алгоритм посимвольного решения, основанный на критерии максимума апосте­риорной вероятности и наблюдении последовательно­сти сигнальных интервалов (рис. 3). Данный алгоритм основан на методе апостериорной вероятности (МАВ) и минимизирует среднюю вероятность ошибочного приема каждого символа. Оптимальная версия алго­ритма описана в [2] и является сложной итеративной процедурой, не реализуемой на практике. Однако су­ществуют субоптимальные варианты реализации дан­ного алгоритма, которые используются непосред­ственно для демодуляции ЧМНФ-сигналов.

Предположим, что на i-ом сигнальном интервале времени наблюдается текущая реализация сигнала y(t) и на D символов в будущем. Вычислим корреля­ционные интегралы между поступившим сигналом у(t) и локально генерируемыми реализациями , соответствующими 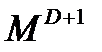всевозможным комбинациям символов в кодовой последовательно­сти длиной n=D+1:

Рис. 3. Блок-схема когерентного последовательного демодулятора ЧМНФ

Корреляторы объединяются в М групп по М ^n-1 таким образом, чтобы кодовые комбинации генерируемых символов содержали одинаковый символ на первой позиции. Решение на i-ом сигнальном интервале ба­зируется на взаимных корреляциях на i,i+1,...,D интер­валах. Выход каждого коррелятора подвергается эк­споненциальному преобразованию и усредняется по всей группе. Решение о символе, переданном на /-ом интервале, то есть D интервалов назад от последнего полученного символа, принимается по выбору группы, имеющей максимальное накопленное значение. Для бинарной ЧМНФ имеется две группы по 2^n-1 корреля­тора. Установлено [2], что минимум вероятности ошибки достигается при индексе модуляции h=0.715. Можно показать, что при n =2 имеет место улучшение рабочих характеристик демодулятора на 2,5 дБ отно­сительно ортогональной ЧМ. При n=3 выигрыш до­стигается до 4 дБ. В [2] отмечено, что дальнейшее расширение интервала корреляции ведет к относи­тельно малому выигрышу.

Известна еще одна реализация данного алгорит­ма, имеющая аналогичные рабочие характеристики, в которой решение о символе, поступившем на i-ом сигнальном интервале принимается по нахождению максимального выхода каждого из M^D+I коррелято­ров, что вносит некоторое упрощение путем удале­ния сумматоров и экспоненциальных преобразовате­лей. Однако эта оценка является максимально пра­вдоподобной.

Основной недостаток рассмотренных алгоритмов посимвольного детектирования заключается в том, что последние требуют точного знания фазы несущей в начале интервала корреляции, что в условии малых отношений сигнал/шум затруднено. Однако возмож­но предположить, что на интервале корреляции фаза несущей равномерно распределена на интервале (0..2п) и провести усреднение по фазе. Так возможно осуществить когерентное интегрирование по и сиг­нальным интервалам, но выход корреляторов продетектировать по огибающей. Таким образом, прихо­дим к реализации некогерентного демодулятора ЧМНФ-сигналов.

Оптимизация рабочих характеристик данной схе­мы [2] достигается выбором нечетного значения n и выполнения решения по среднему символу. Исследо­вания показали, что рабочие характеристики некоге­рентного посимвольного детектора не существенно отличаются от когерентного.

При n=1 данная схема соответствует некогерент­ному квадратурному детектору. Следовательно, при n=3 рассмотренный некогерентный последовательностный алгоритм при фиксированной вероятности ошибки по сравнению с некогерентным квадратур­ным детектором имеет выигрыш не менее 3 дБ.

Основные преимущества рассмотренной группы ал­горитмов заключены в высоких рабочих характеристи­ках, сравнимых с декодером максимального правдопо­добия на основе алгоритма Витерби, который будет рассмотрен в следующей статье. Выигрыш по сравне­нию с оптимальным приемом, не отслеживающим свя­зи между фазами символов, достигает 4 дБ (при n=3).

Недостатки алгоритма заключены в том, что при приемлемой вычислительной сложности (при n=2) алгоритм требует точного знания фазы несущей сиг­нала в начале каждого сигнального интервала. В не­когерентной версии алгоритма уже значительно воз­растает вычислительная сложность, т.к. для его реа­лизации требуется уже 8 корреляционных каналов и детекторов огибающей.

Окончательное решение о выборе схемы демодулятора может быть принято по результатам имита­ционного моделирования работы алгоритмов в усло­виях реального канала.