Арифметика и алгебра
Действия со степенями

|
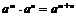
| 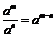
| 
| 
| 
| 
| |

| 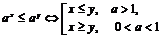
| 
| |||||
Формулы сокращенного умножения
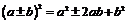
| 
|
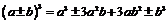
| 
|
Корни квадратного уравнения 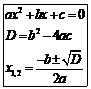
| Выделение полного квадрата в квадратном трехчлене 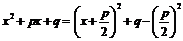
|
Действия с логарифмами

| 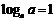
| 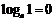
| 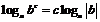
| 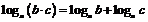
| ||

| 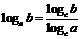
| 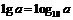
| 
| |||
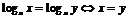
| 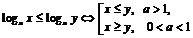
| 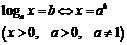
| ||||
| Полярная система координат | |
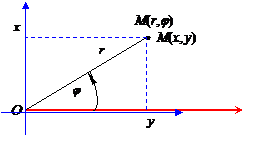
| 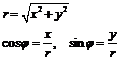
|
 |

Тригонометрия
Основные соотношения
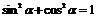
| 
| 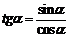
| 
| 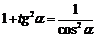
| 
|
Сумма и разность двух аргументов Четность/ нечетность
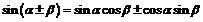
| 
|
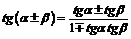
| 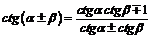
|
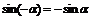
| 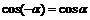
|
Двойные аргументы
| Формулы понижения степени
|
Преобразование произведения в сумму
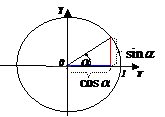
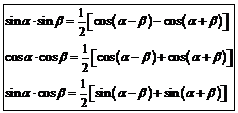
Преобразование суммы и разности в произведение
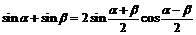
|  
|

| 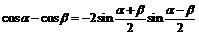
|
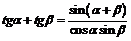
| 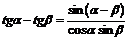
|
Основные значения

| 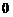
| 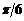
| 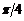
| 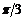
| 
|

| 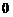
| 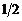
| 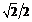
| 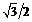
| 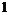
|
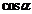
| 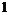
| 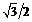
| 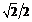
| 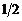
| 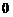
|

| 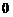
| 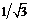
| 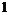
| 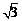
| 
|
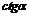
| 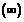
| 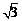
| 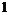
| 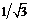
| 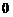
|

| 
| 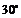
| 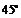
| 
| 
|

|
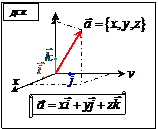
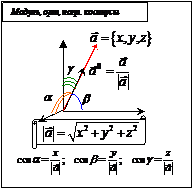
 Векторы
Векторы
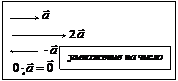

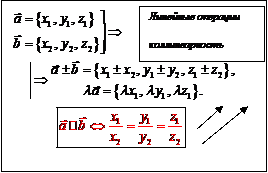

| Скалярное произведение (ЧИСЛО) | Векторное произведение (ВЕКТОР) | Смешанное произведение (ЧИСЛО) |
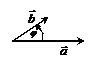 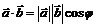
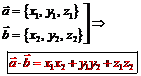
 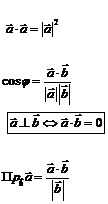
|  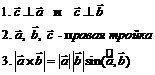 . .

 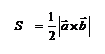 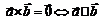
| 

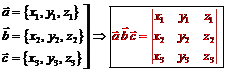
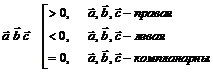

|
Прямая на плоскости (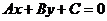 ) )
| |||||
| По точке и нормальному в-ру | 
| По точке и направляющему в-ру | 
| ||
| По точке и угловому коэффициенту | 
| По двум точкам | 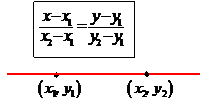
| ||
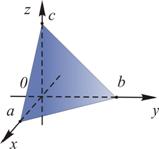
В отрезках на осях 
| 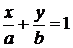
| Вертикаль | 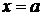
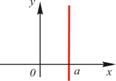
| Горизонталь |  
|
| Взаимное расположение прямых | ||||||

| 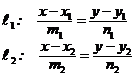
| 
| ||||
  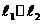
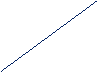
|
  
|   
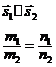
|    

| |||
 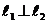
 
| 
| 
| 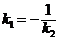
| |||
  
| 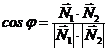
| 
| 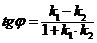
|
Кривые второго порядка ( ) )
| |||
| окружность | 


| эллипс |   
|
| парабола |  
| гипербола |  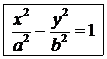 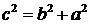
|
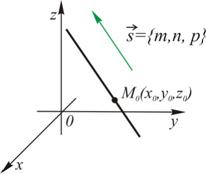
| Прямая и плоскость в пространстве | |
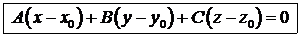 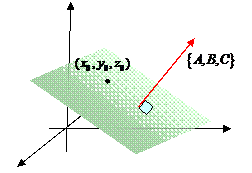
|  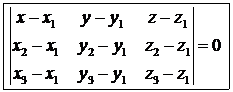
|
 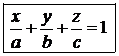
|  
|
 
| 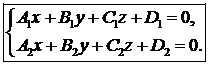 
|
| Поверхности второго порядка | |||||
 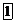 Сфера Сфера 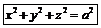
|  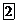 Эллипсоид Эллипсоид 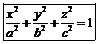
| ||||
 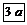 Однополостный гиперболоид Однополостный гиперболоид
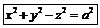
|   Двуполостный гиперболоид. Двуполостный гиперболоид.

| ||||
 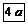 Круговой параболоид. Круговой параболоид.
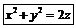
| 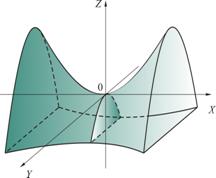 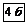 Гиперболический параболоид Гиперболический параболоид 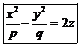 (p>0, q>0).
(p>0, q>0).
| ||||
 Круговой конус: Круговой конус:
 
|   Цилиндрическая поверхность — поверхность, образуемая движением прямой Цилиндрическая поверхность — поверхность, образуемая движением прямой  (называемой образующей) вдоль кривой (называемой образующей) вдоль кривой  (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
(В каноническом уравнении отсутствует одна из переменных) (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
(В каноническом уравнении отсутствует одна из переменных)
| ||||
Графики основных элементарных функций
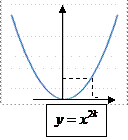
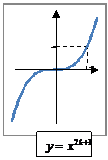
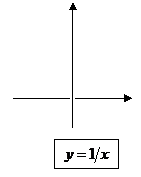
| Постоянная, степенная | 
| 
| 
|   
| 
| |||
| Показательная, логарифмическая | 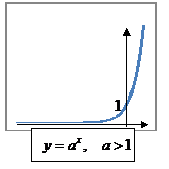 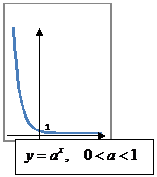
|   
| ||||||
| тригонометрическая |

| 
| ||||||
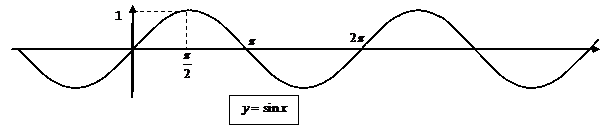
| 
| |||||||
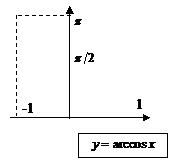
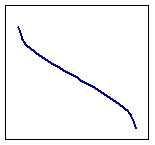
| обратная тригонометрическая |  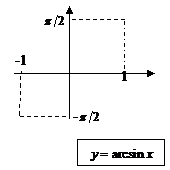 
|  
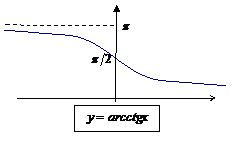
| ||||||
Замечательные пределы
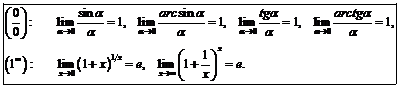
Эквивалентные б.м. при 
| ||
 ~ ~ 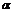
| 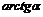 ~ ~ 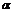
| 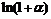 ~ ~ 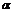
|
 ~ ~ 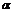
| 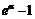 ~ ~ 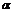
| 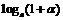 ~ ~ 
|
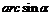 ~ ~ 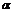
|  ~ ~ 
| 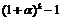 ~ ~ 
|
Производные некоторых элементарных функций
| 1. | 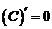
| 
| 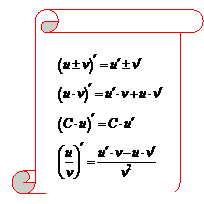
|
| 2. |  
| 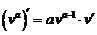
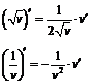
| |
| 3. |   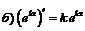
| 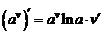 
| 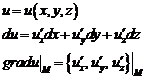
|
| 4. | 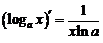 
| 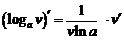 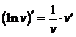
| 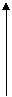 
    Z Z
    Y
X Y
X
|
| 5. | 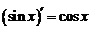 
| 
| |
| 6. |  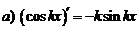
| 
| |
| 7. | 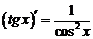
| 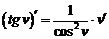
| Лок. экстремум
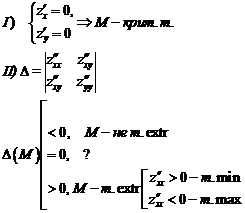
|
| 8. | 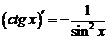
| 
| |
| 9. | 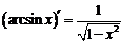
| 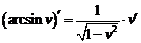
| |
| 10. | 
| 
| |
| 11. | 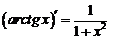
| 
| |
| 12. | 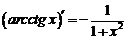
| 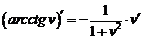
|
Интегралы некоторых элементарных функций

| 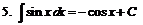 
|  
| ||||||
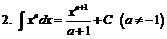 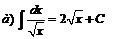 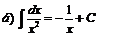
| ||||||||
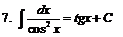 
| ||||||||
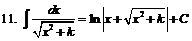 
| ||||||||

|  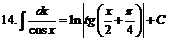
| |||||||
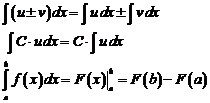
| ||||||||
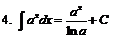 
| ||||||||
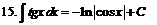 
| ||||||||
  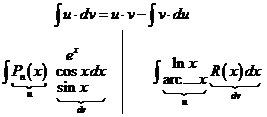
| 
| 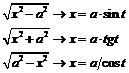
| ||||||
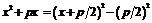
| ||||||||
| 

| |||||||
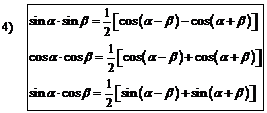 
| 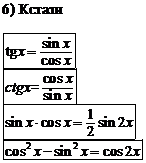
| |||||||
Кратные и криволинейные интегралы
| Двойной интеграл | |||
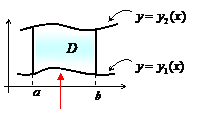 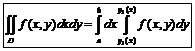
| 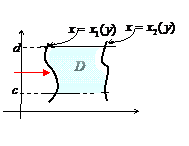 
|  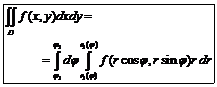
| |
| Тройной интеграл | |||
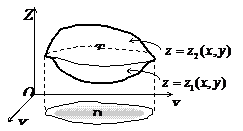
| 
| ||
 Криволинейный интеграл I рода
Криволинейный интеграл I рода 
1  :
: 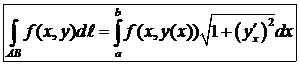 .
.
2. 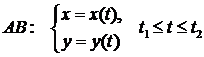 :
: 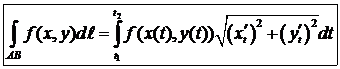 .
.
3. 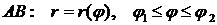 :
: 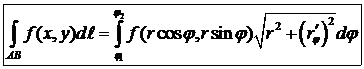 .
.
| 
| 
| 
|

| 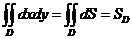
|  -пов. инт.-СРС -пов. инт.-СРС
| 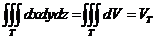
|
ОДУ 1-го порядка 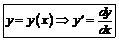
| ДУ с разделенными переменными | Однородные ДУ | Бернулли (линейные) | В полных дифференциалах | |
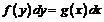
| 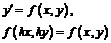
| 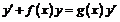
| 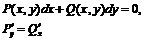
| |
 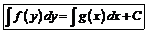
| 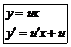
|  или
или
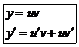
   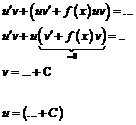
| 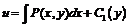

| |
 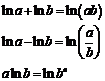 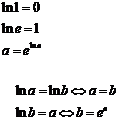
|
ОДУ высших порядков
1. Допускающие понижение порядка
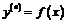
|  (без y) (без y)
| 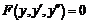 (без x) (без x)
|
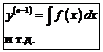
| 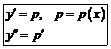
| 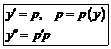
|
2. Линейные ДУ с постоянными коэффициентами
Однородные
Составляем х. у.
| ||||||||||||||||||
Неоднородные 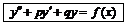 Общее решение
Общее решение 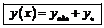 . .
| ||||||||||||||||||
Метод вариации

| ||||||||||||||||||
Правая часть специального вида
Здесь |
Или
 где
где 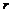 – кратность с корня – кратность с корня 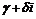 в х.у.; в х.у.;  вещ. многочлены; вещ. многочлены; 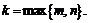
|
ЧИСЛОВЫЕ РЯДЫ
Знакоположительные ряды 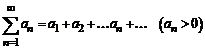
| .Необходимый признак сходимости | Геометрическая прогрессия | Ряд Дирихле |

| 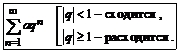
| 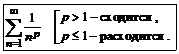
|
Теорема сравнения 1. 
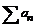 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Теорема сравнения 2. 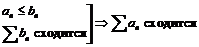 .
.
Теорема сравнения 3.  .
.
Признак Даламбера.  .
.
Радикальный признак Коши
 .
.
Интегральный признак Коши. Если существует непрерывная монотонно убывающая на  функция
функция  , такая что
, такая что 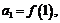
 , то ряд
, то ряд 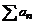 и интеграл
и интеграл 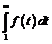 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Знакочередующиеся ряды. 
Теорема Лейбница. 
 сходится.
сходится.
Если ряд 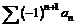 сходится и ряд
сходится и ряд  сходится, то говорят, что ряд
сходится, то говорят, что ряд 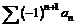 сходится а бсолютно.
сходится а бсолютно.
Если ряд 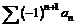 сходится, а ряд
сходится, а ряд  расходится, то говорят, что ряд
расходится, то говорят, что ряд 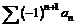 сходится условно.
сходится условно.
Если ряд 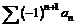 сходится, то
сходится, то 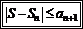 ..
..
Ряд Тейлора
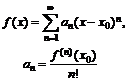
|
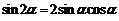
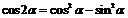

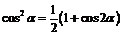

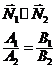

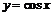
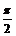


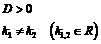

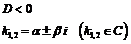

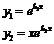
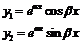
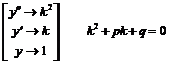 .
. 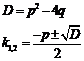 .
. .
.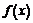


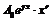
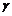
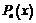

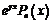
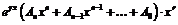
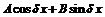
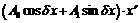
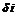
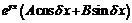

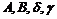 – заданы,
– заданы,  – неизвестные, подлежащие вычислению,
– неизвестные, подлежащие вычислению,