Отделение корней
Во многих приближённых методах нахождения корня уравнения  заранее требуется знать какой-либо отрезок
заранее требуется знать какой-либо отрезок  , на котором лежит искомый корень
, на котором лежит искомый корень  , и притом только один этот корень (то есть предъявляемый отрезок не должен содержать других корней уравнения
, и притом только один этот корень (то есть предъявляемый отрезок не должен содержать других корней уравнения  ). В этом случае говорят, что корень
). В этом случае говорят, что корень  отделён на отрезке
отделён на отрезке  . Отделить корень – значит указать такой отрезок, на котором корень отделён. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.
. Отделить корень – значит указать такой отрезок, на котором корень отделён. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.
Кроме того, часто нужно знать начальное приближение 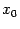 к корню
к корню  (который, заметим, неизвестен). В качестве этого начального приближения берут, как правило, любую точку отрезка, на котором отделён корень, например, его середину
(который, заметим, неизвестен). В качестве этого начального приближения берут, как правило, любую точку отрезка, на котором отделён корень, например, его середину  , если описание метода не предписывает поступить как-нибудь иначе.
, если описание метода не предписывает поступить как-нибудь иначе.
Метод простого перебора
Пусть задана точность  , с которой мы хотим приближённо найти корень
, с которой мы хотим приближённо найти корень  . Это означает, что мы должны предъявить в качестве результата вычислений известное число
. Это означает, что мы должны предъявить в качестве результата вычислений известное число  , которое отличается от истинного значения корня
, которое отличается от истинного значения корня  (которое нам неизвестно) не более чем на
(которое нам неизвестно) не более чем на  :
:  .
.
Пусть искомый корень  отделён на отрезке
отделён на отрезке  .
.
Самый простой (но и самый медленный) способ отыскать  -- взять шаг
-- взять шаг  и перебирать значения
и перебирать значения  с шагом
с шагом  до тех пор, пока функция не сменит знак (по сравнению со знаком исходного числа
до тех пор, пока функция не сменит знак (по сравнению со знаком исходного числа  . Последовательно получаем:
. Последовательно получаем:  ;
;  ;
;  . Вычисления продолжаются, пока
. Вычисления продолжаются, пока  . Как только мы получим
. Как только мы получим  , нужно взять за приближённое значение корня середину между последними двумя точками:
, нужно взять за приближённое значение корня середину между последними двумя точками:  . Поскольку по теореме о корне непрерывной функции
. Поскольку по теореме о корне непрерывной функции  , а длина этого сегмента
, а длина этого сегмента  , то
, то  , то есть корень найден с нужной точностью.
, то есть корень найден с нужной точностью.
|
|

1. Рис.9.1.Перебор значений функции, до тех пор пока она не сменит знак
Недостатком метода, конечно, является необходимость большого количества вычислений функции  . Считая шаг
. Считая шаг  малым и предполагая, что в среднем корень будет обнаруживаться где-то вблизи середины отрезка, мы можем предположить, что среднее количество вычислений функции, которое нам понадобится до нахождения
малым и предполагая, что в среднем корень будет обнаруживаться где-то вблизи середины отрезка, мы можем предположить, что среднее количество вычислений функции, которое нам понадобится до нахождения  , составит
, составит
1 
В случае, если это вычисление занимает слишком много времени, метод становится совершенно непригодным. Однако, при увеличивающемся быстродействии вычислительной техники, когда нам становится не так уж важно, сколько именно времени займёт вычисление  в очередной точке (всё равно немного!), привлекательность метода повышается: уж очень он прост и, кроме того, совершенно нетребователен к гладкости функции, достаточно лишь, чтобы она была непрерывной.
в очередной точке (всё равно немного!), привлекательность метода повышается: уж очень он прост и, кроме того, совершенно нетребователен к гладкости функции, достаточно лишь, чтобы она была непрерывной.
Пример 9.4 Рассмотрим уравнение  , корень которого был нами отделён на отрезке
, корень которого был нами отделён на отрезке  . Пусть корень
. Пусть корень  требуется определить с точностью
требуется определить с точностью  . Возьмём шаг
. Возьмём шаг  равным
равным  , то есть
, то есть  . Тогда, вычисляя последовательно значения функции в точках
. Тогда, вычисляя последовательно значения функции в точках  , получаем:
, получаем:

При переходе от  к
к  функция сменила знак. Следовательно, корень приближённо равен
функция сменила знак. Следовательно, корень приближённо равен  с точностью
с точностью  . При этом нам понадобилось вычислить значение функции
. При этом нам понадобилось вычислить значение функции  17 раз. Можно сказать, повезло: ведь оценка количества вычислений даёт
17 раз. Можно сказать, повезло: ведь оценка количества вычислений даёт  .
.
|
|
Метод простых итераций
Предположим, что уравнение  при помощи некоторых тождественных преобразований приведено к виду
при помощи некоторых тождественных преобразований приведено к виду  .
.
Заметим, что такое преобразование можно вести разными способами, и при этом будут получаться разные функции  в правой части уравнения. Уравнение
в правой части уравнения. Уравнение  эквивалентно уравнению
эквивалентно уравнению  при любой функции
при любой функции  . Таким образом, можно взять
. Таким образом, можно взять  и при этом выбрать функцию (или постоянную)
и при этом выбрать функцию (или постоянную)  так, чтобы функция
так, чтобы функция  удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения корня уравнения.
удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения корня уравнения.
Для нахождения корня уравнения  выберем какое-либо начальное приближение
выберем какое-либо начальное приближение 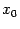 (расположенное, по возможности, близко к корню
(расположенное, по возможности, близко к корню  ). Далее будем вычислять последующие приближения
). Далее будем вычислять последующие приближения

по формулам

то есть используя каждое вычисленное приближение к корню в качестве аргумента функции  в очередном вычислении. Такие вычисления по одной и той же формуле
в очередном вычислении. Такие вычисления по одной и той же формуле  , когда полученное на предыдущем шаге значение используется на последующем шаге, называются итерациями. Итерациями называют часто и сами значения
, когда полученное на предыдущем шаге значение используется на последующем шаге, называются итерациями. Итерациями называют часто и сами значения  , полученные в этом процессе (то есть, в нашем случае, последовательные приближения к корню).
, полученные в этом процессе (то есть, в нашем случае, последовательные приближения к корню).
Заметим: тот факт, что  -- корень уравнения
-- корень уравнения  , означает, что
, означает, что  есть абсцисса точки пересечения графика
есть абсцисса точки пересечения графика  с прямой
с прямой 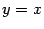 . Если же при каком-либо
. Если же при каком-либо 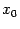 вычислено значение
вычислено значение 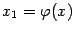 и взято в качестве нового аргумента функции, то это означает, что через точку графика
и взято в качестве нового аргумента функции, то это означает, что через точку графика  проводится горизонталь до прямой
проводится горизонталь до прямой 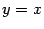 , а оттуда опускается перпендикуляр на ось
, а оттуда опускается перпендикуляр на ось  . Там и будет находиться новый аргумент
. Там и будет находиться новый аргумент 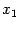 .
.

2. Рис.9.3.Точка  -- решение уравнения
-- решение уравнения  . Построение точки
. Построение точки 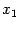 по точке
по точке 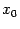
|
|
Проследим, как изменяются последовательные приближения  при различных вариантах взаимного расположения графика
при различных вариантах взаимного расположения графика  и прямой
и прямой 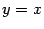 .
.
1). График  расположен, по крайней мере в некоторой окрестности корня, включающей начальное приближение
расположен, по крайней мере в некоторой окрестности корня, включающей начальное приближение 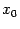 , в некотором угле со сторонами, имеющими наклон менее
, в некотором угле со сторонами, имеющими наклон менее 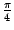 к горизонтали (то есть стороны угла -- прямые
к горизонтали (то есть стороны угла -- прямые  , где
, где  ):
):



3. Рис.9.4.График пересекает прямую 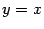 под малым углом: варианты расположения
под малым углом: варианты расположения
Если предположить вдобавок, что функция  имеет производную
имеет производную  , то этот случай соответствует тому, что выполнено неравенство
, то этот случай соответствует тому, что выполнено неравенство  , при
, при  , близких к корню
, близких к корню  . Проследим в этом случае за поведением последовательных приближений
. Проследим в этом случае за поведением последовательных приближений 

4. Рис.9.5.Сходящиеся к корню приближения в случае  : два варианта
: два варианта
Мы видим, что каждое следующее приближение  будет в этом случае расположено ближе к корню
будет в этом случае расположено ближе к корню  , чем предыдущее приближение
, чем предыдущее приближение  . При этом, если график при
. При этом, если график при 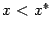 лежит ниже горизонтали
лежит ниже горизонтали  , а при
, а при  -- выше её (что, в случае наличия производной, верно, если
-- выше её (что, в случае наличия производной, верно, если  ), то приближения
), то приближения  ведут себя монотонно: если
ведут себя монотонно: если  , то последовательность
, то последовательность  монотонно возрастает и стремится к
монотонно возрастает и стремится к  , а если
, а если  , то монотонно убывает и также стремится к
, то монотонно убывает и также стремится к  . Если же график функции
. Если же график функции  лежит выше горизонтали
лежит выше горизонтали  при
при 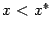 и ниже её при
и ниже её при  (это так, если
(это так, если  ), то последовательные приближения
), то последовательные приближения  ведут себя иначе: они "скачут" вокруг корня
ведут себя иначе: они "скачут" вокруг корня  , с каждым скачком приближаясь к нему, но так же стремятся к
, с каждым скачком приближаясь к нему, но так же стремятся к  при
при  .
.
Заметим, что если функция  не монотонна в окрестности точки
не монотонна в окрестности точки  , то последовательные приближения могут вести себя нерегулярно (то есть не монотонно и не оказываясь попеременно то левее, то правее корня, а делая скачки относительно корня при произвольных номерах (см. следующий чертёж):
, то последовательные приближения могут вести себя нерегулярно (то есть не монотонно и не оказываясь попеременно то левее, то правее корня, а делая скачки относительно корня при произвольных номерах (см. следующий чертёж):

5. Рис.9.6.В случае немонотонной функции  сходящиеся итерации могут вести себя нерегулярно
сходящиеся итерации могут вести себя нерегулярно
2). График  расположен, по крайней мере в некоторой окрестности корня, вне некоторого угла со сторонами, имеющими наклон более
расположен, по крайней мере в некоторой окрестности корня, вне некоторого угла со сторонами, имеющими наклон более 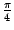 к горизонтали (то есть стороны угла -- прямые
к горизонтали (то есть стороны угла -- прямые  , где
, где  ):
):

6. Рис.9.7.График пересекает прямую 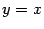 под большим углом: варианты расположения
под большим углом: варианты расположения
Если функция  имеет производную
имеет производную  , то в этом случае при
, то в этом случае при  , близких к корню
, близких к корню  , выполнено неравенство
, выполнено неравенство  .
.

7. Рис.9.8.Числа  расходятся в случае
расходятся в случае  : два варианта
: два варианта
Каждая следующая итерация  будет в этом случае расположена дальше от корня
будет в этом случае расположена дальше от корня  , чем предыдущая,
, чем предыдущая,  . При этом, в зависимости от того, пересекает ли график прямую
. При этом, в зависимости от того, пересекает ли график прямую 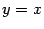 "снизу вверх" или "сверху вниз" (см. рис.), последовательность
"снизу вверх" или "сверху вниз" (см. рис.), последовательность  монотонно удаляется от корня
монотонно удаляется от корня  или же итерации удаляются от
или же итерации удаляются от  , оказываясь попеременно то справа, то слева от корня.
, оказываясь попеременно то справа, то слева от корня.
Ещё одно замечание: если не выполнено ни условие  , ни условие
, ни условие  , то итерации
, то итерации  могут зацикливаться. На чертеже ниже приведён пример зацикливания, когда уравнение имеет вид
могут зацикливаться. На чертеже ниже приведён пример зацикливания, когда уравнение имеет вид  .
.

8. Рис.9.9.Пример зацикливания итераций
Мы видим, что для сходимости итераций к корню, вообще говоря, не обязательно наличие производной у функции  . Однако метод итераций гораздо удобнее формулировать в терминах, связанных со значениями производной. Именно так мы и сформулируем наши наблюдения в виде теоремы.
. Однако метод итераций гораздо удобнее формулировать в терминах, связанных со значениями производной. Именно так мы и сформулируем наши наблюдения в виде теоремы.
Теорема 9.3 Если функция  имеет производную в некоторой окрестности
имеет производную в некоторой окрестности  корня
корня  уравнения
уравнения  , причём
, причём  при
при  , то последовательность итераций
, то последовательность итераций  , полученных при
, полученных при  , начиная с
, начиная с  , сходится к корню
, сходится к корню  .
.
При этом скорость сходимости задаётся неравенствами

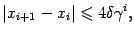
где  -- длина окрестности
-- длина окрестности  , а точность
, а точность  -го приближения -- оценкой
-го приближения -- оценкой

Доказательство. Пусть  . По формуле конечных приращений, применённой к отрезку между точками
. По формуле конечных приращений, применённой к отрезку между точками 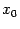 и
и  , получаем
, получаем

где  лежит между
лежит между 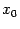 и
и  . Значит,
. Значит,

то есть
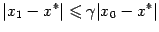
(напомним, что  и
и  ). Повторяя рассуждения для точек
). Повторяя рассуждения для точек  вместо
вместо 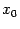 , получаем:
, получаем:

| |

| |

| |

| |

| |

|
Так как  , последовательность
, последовательность  стремится к 0 при
стремится к 0 при  . Значит,
. Значит,  при
при  .
.
Неравенство  очевидно, поскольку из того, что
очевидно, поскольку из того, что 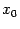 и
и  лежат в окрестности
лежат в окрестности  длины
длины  , следует, что
, следует, что  .
.
Поскольку

мы имеем

так как  и
и 
Определение 9.1 Доказанные оценки показывают, что скорость сходимости итераций к корню не меньше, чем у геометрической прогрессии со знаменателем  , где
, где  -- величина, ограничивающая сверху абсолютную величину производной. Тем самым, чем меньше
-- величина, ограничивающая сверху абсолютную величину производной. Тем самым, чем меньше  , тем быстрее сходятся итерации. Наиболее быстро они будут сходиться, если график
, тем быстрее сходятся итерации. Наиболее быстро они будут сходиться, если график  пересекает прямую
пересекает прямую 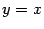 , имея горизонтальную касательную, то есть при
, имея горизонтальную касательную, то есть при  (и, разумеется, при выборе начального приближения
(и, разумеется, при выборе начального приближения 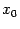 достаточно близко к корню
достаточно близко к корню  , так чтобы на отрезке между
, так чтобы на отрезке между 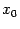 и
и  производная мало отличалась от 0).
производная мало отличалась от 0).

9. Рис.9.10.Быстрая сходимость итераций при горизонтальной касательной к графику
Выше мы отмечали, что привести уравнение  к виду
к виду  можно, выбирая
можно, выбирая  в виде
в виде  , где
, где  -- произвольная функция. При различных способах выбора
-- произвольная функция. При различных способах выбора 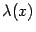 получаются разные модификации метода итераций, которые имеют отличающиеся свойства: разную скорость сходимости (но не меньшую той, что гарантирована теоремой) и разную потребность в вычислении значений функции
получаются разные модификации метода итераций, которые имеют отличающиеся свойства: разную скорость сходимости (но не меньшую той, что гарантирована теоремой) и разную потребность в вычислении значений функции  или
или  , а также их производных.
, а также их производных.
Метод секущих
В качестве функции 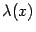 берут любую постоянную
берут любую постоянную  , знак которой совпадает со знаком производной
, знак которой совпадает со знаком производной  в окрестности
в окрестности  (и, в частности, на отрезке, соединяющем
(и, в частности, на отрезке, соединяющем 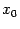 и
и  ). Постоянная
). Постоянная  не зависит также и от номера шага
не зависит также и от номера шага  . Тогда формула итераций оказывается очень проста:
. Тогда формула итераций оказывается очень проста:
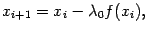
и на каждой итерации нужно один раз вычислить значение функции  .
.
Выясним смысл этой формулы, а также смысл условия о совпадении знаков  и
и  . Рассмотрим прямую, проходящую через точку
. Рассмотрим прямую, проходящую через точку 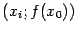 на графике
на графике  с угловым коэффициентом
с угловым коэффициентом  . Тогда уравнением этой прямой будет
. Тогда уравнением этой прямой будет
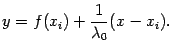
Найдём точку пересечения этой прямой с осью  из уравнения
из уравнения
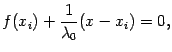
откуда  . Следовательно, эта прямая пересекает ось
. Следовательно, эта прямая пересекает ось  как раз в точке следующего приближения. Тем самым получаем следующую геометрическую интерпретацию последовательных приближений. Начиная с точки
как раз в точке следующего приближения. Тем самым получаем следующую геометрическую интерпретацию последовательных приближений. Начиная с точки 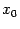 , через соответствующие точки графика
, через соответствующие точки графика  проводятся секущие с угловым коэффициентом
проводятся секущие с угловым коэффициентом  того же знака, что производная
того же знака, что производная  . (Заметим, что, во-первых, значение производной вычислять не обязательно, достаточно лишь знать, убывает функция
. (Заметим, что, во-первых, значение производной вычислять не обязательно, достаточно лишь знать, убывает функция  или возрастает; во-вторых, что прямые, проводимые при разных
или возрастает; во-вторых, что прямые, проводимые при разных  , имеют один и тот же угловой коэффициент
, имеют один и тот же угловой коэффициент  и, следовательно, параллельны друг другу.) В качестве следующего приближения к корню берётся точка пересечения построенной прямой с осью
и, следовательно, параллельны друг другу.) В качестве следующего приближения к корню берётся точка пересечения построенной прямой с осью  .
.

10. Рис.9.11.Последовательные итерации метода секущих
На чертеже слева изображены итерации при  , в случае
, в случае  и в случае
и в случае  . Мы видим, что в первом случае меняющаяся точка
. Мы видим, что в первом случае меняющаяся точка  уже на первом шаге "перепрыгивает" по другую сторону от корня
уже на первом шаге "перепрыгивает" по другую сторону от корня  , и итерации начинают приближаться к корню с другой стороны. Во втором случае последовательные точки
, и итерации начинают приближаться к корню с другой стороны. Во втором случае последовательные точки  приближаются к корню, оставаясь всё время с одной стороны от него. (Исследуйте сами, как выглядит процесс в случае
приближаются к корню, оставаясь всё время с одной стороны от него. (Исследуйте сами, как выглядит процесс в случае  , то есть когда функция
, то есть когда функция  убывает.)
убывает.)
Достаточное условие сходимости, которое нам даёт теорема 9.3, таково:

Это неравенство можно записать в виде

откуда получаем, что сходимость гарантируется, когда, во-первых,

так как  (тем самым проясняется смысл выбора знака числа
(тем самым проясняется смысл выбора знака числа  ), а во-вторых, когда
), а во-вторых, когда  при всех
при всех  на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если
на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если

где  . Таким образом, угловой коэффициент
. Таким образом, угловой коэффициент  не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка
не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка 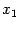 может выскочить из рассматриваемой окрестности корня
может выскочить из рассматриваемой окрестности корня  , и сходимость итераций к корню может быть нарушена.
, и сходимость итераций к корню может быть нарушена.
Метод одной касательной
Заметим, что в методе секущих удобно было бы фиксировать наиболее удобное для первого шага значение 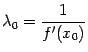 , при котором все секущие параллельны касательной, проведённой к графику
, при котором все секущие параллельны касательной, проведённой к графику  при
при  . При таком выборе
. При таком выборе  метод секущих называется методом одной касательной. Формула итераций этого метода имеет вид
метод секущих называется методом одной касательной. Формула итераций этого метода имеет вид
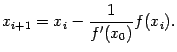
Как видно из этой формулы, производную придётся вычислить только один раз, а затем на каждом шаге использовать значение 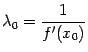 или, что то же,
или, что то же,  .
.

11. Рис.9.12.Итерации метода одной касательной
При таком выборе  в точке
в точке 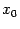 выполнено равенство
выполнено равенство

и если отрезок, на котором отделён корень и выбрано начальное приближение 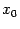 , достаточно мал, а производная
, достаточно мал, а производная  непрерывна, то значение
непрерывна, то значение 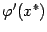 будет не сильно отличаться от
будет не сильно отличаться от  и, следовательно, график
и, следовательно, график  будет пересекать прямую
будет пересекать прямую 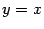 , идя почти горизонтально. А это, как мы отмечали выше, будет давать нам быстрое приближение итераций к корню (так как число
, идя почти горизонтально. А это, как мы отмечали выше, будет давать нам быстрое приближение итераций к корню (так как число  при этом можно выбрать равным
при этом можно выбрать равным 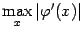 , а эта величина мала).
, а эта величина мала).
Пример 9.6 Решим методом одной касательной уравнение  . (Напомним, что его корень был ранее нами отделён на отрезке
. (Напомним, что его корень был ранее нами отделён на отрезке  .) Корень будем находить с точностью до
.) Корень будем находить с точностью до  , а для этого вычисления будем вести до тех пор, пока в значении
, а для этого вычисления будем вести до тех пор, пока в значении  не зафиксируется шестой знак после десятичного разделителя.
не зафиксируется шестой знак после десятичного разделителя.
В качестве начального приближения возьмём  . Поскольку
. Поскольку

то  и
и  . Значит, итерационная формула будет такой:
. Значит, итерационная формула будет такой:

По этой формуле последовательно получаем:

| |

| |

|
Восьмое и девятое приближения уже совпадают с точностью  , поэтому вычисления на этом прекращаем и полагаем
, поэтому вычисления на этом прекращаем и полагаем  .
.
Метод Ньютона (метод касательных)
Рассмотрение предыдущего метода позволяет предположить, что итерации станут приближаться к корню ещё быстрее, если мы будем выбирать касательную вместо секущей не только на первом, а на каждом шаге. Ясно, что тогда формула итераций будет иметь вид

| (9.1) |
(сравните с формулой метода одной касательной). Этот метод называется методом касательных, или методом Ньютона. Действительно, последовательные приближения метода Ньютона сходятся гораздо быстрее, чем в общем методе итераций (скорость сходимости приближений в котором, напомним, та же, что у геометрической прогрессии со знаменателем  при
при  ).
).
Поскольку для метода Ньютона

то

В точке  получаем
получаем  , так как
, так как  . Тем самым, в этом методе график
. Тем самым, в этом методе график  пересекает прямую
пересекает прямую 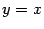 в точности по горизонтали, что приводит к очень быстрой сходимости итераций к
в точности по горизонтали, что приводит к очень быстрой сходимости итераций к  . Именно, имеет место оценка
. Именно, имеет место оценка

| (9.2) |
где  -- некоторая постоянная (не зависящая от
-- некоторая постоянная (не зависящая от  ). Если начальное приближение
). Если начальное приближение 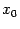 взято достаточно близко от корня
взято достаточно близко от корня  , то можно взять
, то можно взять  .Заметим, что по сравнению с общей оценкой метода итераций
.Заметим, что по сравнению с общей оценкой метода итераций
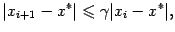
постоянная  заменяется в оценке метода Ньютона (9.2) на стремящуюся к 0 величину
заменяется в оценке метода Ньютона (9.2) на стремящуюся к 0 величину  ; отсюда и высокая скорость сходимости.
; отсюда и высокая скорость сходимости.
Доказательство оценки (9.2) можно найти в учебниках, специально посвящённых численным методам, например, [Амосов А. А., Дубинский Ю. А., Копченова Н. В. Вычислительные методы для инженеров. -- М.: Высш. шк., 1994], [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М.Численные методы. -- М.: Наука, 1987], [Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. -- М.: Наука, 1986].
Скорость сходимости итераций, которая задаётся формулой (9.2), называется квадратичной. Квадратичная скорость сходимости означает, примерно говоря, что число верных знаков в приближённом значении  удваивается с каждой итерацией. Действительно, если
удваивается с каждой итерацией. Действительно, если  , и
, и  , то
, то 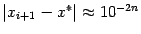 . Это и означает, что число верных знаков при переходе к следующему приближению возросло с
. Это и означает, что число верных знаков при переходе к следующему приближению возросло с  до
до  , то есть удвоилось.
, то есть удвоилось.
Геометрический смысл метода Ньютона состоит в том, что на каждом шаге мы строим касательную к графику  в точке очередного последовательного приближения
в точке очередного последовательного приближения  , а за следующее приближение
, а за следующее приближение  берём точку пересечения этой касательной с осью
берём точку пересечения этой касательной с осью  . Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).
. Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).

12. Рис.9.13.Последовательные приближения метода Ньютона
Заметим, что по-другому идею метода Ньютона мы можем описать так: на каждом шаге вместо исходного уравнения  мы решаем приближённое, линеаризованное в точке
мы решаем приближённое, линеаризованное в точке  уравнение
уравнение

в котором левая часть -- это многочлен Тейлора первого порядка для функции  в точке
в точке  , то есть линейная функция
, то есть линейная функция

Решением линеаризованного уравнения  служит следующее приближение
служит следующее приближение  , в то время как решением исходного точного уравнения
, в то время как решением исходного точного уравнения  служит искомый корень
служит искомый корень  .
.
Идея замены точной (но сложной) задачи последовательностью более простых линеаризованных задач весьма продуктивна в приближённых методах; например, такая идея даёт эффективный способ решения многомерных задач с ограничениями (метод Франка - Вулфа в нелинейном программировании, см., например, [Киселёв В.Ю., Экономико-математические методы и модели. -- Иваново: изд. ИГЭУ, 1998]).
Пример 9.7 Решим методом Ньютона всё то же уравнение  , взяв в качестве начального приближения
, взяв в качестве начального приближения  и задав точность
и задав точность  (ту же, что была взята при решении этого уравнения методом одной касательной). Поскольку
(ту же, что была взята при решении этого уравнения методом одной касательной). Поскольку  , то итерационная формула метода Ньютона будет такой:
, то итерационная формула метода Ньютона будет такой:

Применяя эту формулу, последовательно находим:

так что  с точностью
с точностью  . Как мы видим, значение корня с нужной нам точностью было получено уже на третьем шаге. (Четвёртый шаг понадобился для того, чтобы можно было убедиться, что с нужной нам точностью значение перестало изменяться.)
. Как мы видим, значение корня с нужной нам точностью было получено уже на третьем шаге. (Четвёртый шаг понадобился для того, чтобы можно было убедиться, что с нужной нам точностью значение перестало изменяться.)