Кривые второго порядка.
Кривой 2-го порядка называется линия, которой соответствует алгебраическое уравнение 2-й степени: Ax2 + Bxy + Cy2 + Dx + Ey + F = 0.
Рассмотрим три вида кривых второго порядка: эллипс, гиперболу и параболу.
Эллипс.
Эллипсом называют множество точек, сумма расстояний которых от двух данных точек 
и 
– фокусов эллипса – есть величина постоянная (2a), большая расстояния между фокусами (2c).
Если центр симметрии эллипса совпадает с началом координат, а фокусы лежат на оси Ох, то уравнение эллипса имеет вид: 
и называется каноническим уравнением эллипса.
Термины и обозначения основных элементов эллипса:
с – фокусное расстояние; а – большая полуось эллипса; b – малая полуось эллипса.
Точки 
, 
; 
, 
называют вершинами эллипса; точки 
и 
– это фокусы эллипса; точка О(0; 0) называется центром эллипса.
Числа a, b, c связаны равенством: 
, причем 
.
Величина 
называется эксцентриситетом эллипса и характеризует степень его сжатости. Если 
, то эллипс вырождается в окружность x2 + y2 = R2 .
Две прямые, перпендикулярные к большой оси эллипса и расположенные относительно центра на расстоянии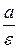 
от него, называются директрисами эллипса. Директриса 
называется левой, а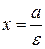 
– правой.
Если центр симметрии эллипса имеет координаты 
, а фокусы лежат на прямой, параллельной оси Ох, то уравнение эллипса имеет вид:
.
Если фокусы эллипса лежат на оси Оу, а центр симметрии совпадает с началом координат, то в каноническом уравнении эллипса 
будет 
, 
, 
и 
, 
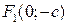– фокусы эллипса.
Если центр симметрии эллипса находится в точке , а фокусы лежат на прямой, параллельной оси Оу, то уравнение эллипса имеет вид: 
.
----------------------------------------------------------------------------------------------------------------
Кривые второго порядка. Стр. 1
Гипербола.
Гиперболой называется множество точек, модуль разности расстояний которых от двух фиксированных точек F1 и F2 (фокусов гиперболы) есть величина постоянная (2a), меньшая расстояния между фокусами (2c).
Если центр симметрии гиперболы совпадает с началом координат, а фокусы лежат на оси Ох, то уравнение гиперболы имеет вид: 
и называется каноническим уравнением гиперболы.
Термины и обозначения основных элементов гиперболы: с – фокусное расстояние; а – ве щественная полуось гиперболы; b – мнимая полуось гиперболы.
Точки и называют вершинами гиперболы, точка О(0;0) называется центром гиперболы; и – это фокусы гиперболы.
Числа a, b, c связаны равенством: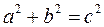 
, причем 
Эксцентриситет, характеризующий степень сжатости гиперболы, равен 
, (
).
Прямоугольник со сторонами 2a и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Диагонали основного прямоугольника (если их неограниченно продолжать) являются асимптотами гиперболы, их уравнения: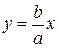 
; 
.
Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоянии 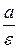от него, называется директрисами гиперболы. Директрисы имеют уравнения: 
.
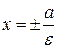Если центр симметрии гиперболы находится в точке , а фокусы лежат на прямой, параллельной оси Ох, то уравнение гиперболы имеет вид:
.
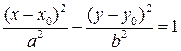Если гипербола симметрична относительно координатных осей, а ее фокусы лежат на оси Оу, то ее каноническое уравнение имеет вид: 
.
В этом случае модуль разности расстояний от любой точки гиперболы до ее фокусов равен 2b, фокусы находятся в точках 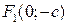, ; эксцентриситет такой гиперболы определяется формулой 
, .
----------------------------------------------------------------------------------------------------------------
Кривые второго порядка. Стр. 2
Если центр симметрии гиперболы находится в точке , а фокусы лежат на прямой, параллельной оси Оу, то ее уравнение: 
.
Если полуоси гиперболы равны, т.е. a=b, то гипербола называется равносторонней (равнобочной).
Парабола.
Параболой называется геометрическое место точек на плоскости, равноудаленных от фиксированной точки 
(фокуса) и данной прямой, не проходящей через эту точку (директрисы), лежащих на этой же плоскости.
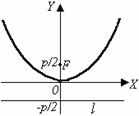
Существуют 4 вида канонических уравнений параболы:
|
х2 = 2ру.
Фокус F(0;  ),
уравнение директрисы: у = – .
|
|
х2 = –2ру.
Фокус F(0; – ),
уравнение директрисы: у = .
|
|
у2 = 2рх.
Фокус F(; 0),
уравнение директрисы: х = – .
|
|
у2 =–2рх.
Фокус F(– ; 0),
уравнение директрисы: х = .
|
Термины и обозначения основных элементов параболы: O – вершина параболы; F – фокус параболы; p – параметр параболы (расстояние от фокуса F до директрисы).
Эксцентриситет параболы равен единице: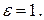 
Если вершина параболы находится в точке , а ее директриса лежит на прямой, параллельной оси Ох, то ее уравнение имеет вид:
или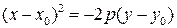 
.
Если вершина параболы находится в точке , а ее директриса лежит на прямой, параллельной оси Оу, то ее уравнение имеет вид:
или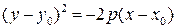 
.
----------------------------------------------------------------------------------------------------------------
Кривые второго порядка. Стр. 3
Задачи для самостоятельного решения.
№1. Составить каноническое уравнение и построить эллипс, большая полуось которого равна 13, а фокус находится в точке F(-5;0).
№2. Составить каноническое уравнение и построить гиперболу, проходящую через точки А(
,3) и В(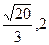
).
№3. Составить каноническое уравнение и построить параболу, имеющую директрису у=1.
№4. Составить каноническое уравнение и построить эллипс, если сумма его полуосей равна 12, а расстояние между фокусами, лежащими на оси Ох, равно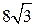 
.
№5. Составить каноническое уравнение и построить гиперболу с вершиной в точке А(2;0) и проходящую через точку В 
.
№6. Составить каноническое уравнение и построить параболу симметричную относительно оси Ох, если расстояние от фокуса до вершины равно 4.
№7. Выделением полных квадратов и переносом начала координат упростите уравнения линий и постройте их:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
;
ж) 
.
Домашнее задание.
№1. Составить каноническое уравнение и построить эллипс, малая полуось которого равна 7, а фокус находится в точке F(13;0).
№2. Составить каноническое уравнение и построить гиперболу, проходящую через точку 
, если её асимптоты имеют уравнения 
.
№3. Составить каноническое уравнение и построить параболу симметричную относительно оси Оу, проходящую через точку А(4;-10).
№4. Выделением полных квадратов и переносом начала координат упростите уравнения линий и постройте их:
а) 
;
б)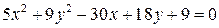 
;
в) 
.
----------------------------------------------------------------------------------------------------------------
Кривые второго порядка. Стр. 4