Методика проведения работы

Лабораторная работа №3

Уширение при прокатке

Общие сведения

При прокатке наряду с уменьшением толщины заготовки (обжатием) и увеличением длины (вытяжкой), происходит увеличение ширины заго­товки (уширение). Под уширением Δb понимают разность между шириной заготовки после прокатки b₁ и до прокатки b₀, т.е.

Δb = b₁ - b₀. (14)

Уширение сопутствует любому процессу прокатки, как в холодном, так и в горячем состоянии.

В большинстве случаев уширение представляет собой отрицательное явление: снижает общую вытяжку при прокатке, способствует утонению кромки. В результате неравномерной деформации в кромках возникают значительные растягивающие напряжения, которые могут вызвать трещи- нообразование.

Уширение при сортовой прокатке используют как средство лучшего заполнения калибра.

Умение рассчитать уширение требуется при горячей прокатке листо­вой заготовки для уменьшения количества боковой обрези, при расчете ширины слитка, а также для правильной установки эджерных валков.

На величину уширения влияет большое количество факторов:

1) величина обжатия;

2) толщина заготовки;

3) число пропусков;

4) температура прокатываемого металла;

5) коэффициент трения;

6) диаметр валков;

7) ширина, полосы.

Для расчета уширения известно большое количество формул, из ко­торых наиболее правильными считаются формулы, выведенные на основа­нии отношения

1п (b₁/b₀)

1п (h₁/h₀)

Одна из таких формул, полученная как следствие основных законов течения пластической среды, имеет вид

 

 

где θ - показатель уширения, который определяют по графику (рис.12).

 

Функция 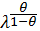представлена в виде номограммы (рис. 13).

 

1 – Δh=0,0-1,0 4 – Δh=2,1-2,5

2 – Δh=1,1-1,5 5 – Δh=2,6-3,0

3 – Δh=1,6-2,0 6 – Δh=3,1-3,5

Рисунок 12 - Графики для определения показателя уширения θ

Рисунок 13 – Номограмма для определения функции λ ^θ/(1-θ)

 

Кроме того, уширение можно рассчитать по формуле Зибеля:

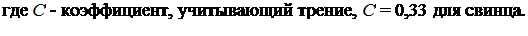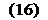
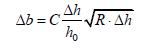
Установлено, что уширение распределяется равномерно по ширине полосы. Однако, рассматривая процесс уширения при прокатке, нужно помнить о законе наименьшего сопротивления, а т. к. периферийные слои полосы встречают меньшее сопротивление своему перемещению в ширину, то они и уширяются больше, что и приводит к появлению растягивающих напряжений и образованию трещин на кромках.

Методика проведения работы

Часть 1. Влияние обжатия на величину уширения

Алюминиевые отожженные (или свинцовые) образцы толщиной h₀ = 3,0; 4,0; 5,0; 7,0 мм, шириной b₀ = 30 мм, длиной 1₀ = 60 мм, прокатывают до толщины h₁ = 2,5 мм на сухих (протертых ацетоном и мелом) валках. Для установки зазо­ра между валками предварительно прокатывают черновой образец. До про­катки образец размечают (рис.14) и измеряют в трех точках ширину, длину между крайними рисками (1₀ = 50 мм) и толщину.

Рисунок 14 – Образец для определения уширения

После прокатки в этих же точках измеряют толщину h₁, длину между крайними рисками, ширину и берут среднее b₁, сравнивают ее с расчетной шириной по формулам (15) и (16). Все данные заносят в табл. 3.1 и строят графики на миллиметровке в координатах b₁ - Δh для рассчитанного и изме­ренного значения b₁.

Таблица 3.1 № образца h0 h1 Δhi, 1о. l1.   λ= l1 / 1о bо. b1 изме-­ b1 расчетная, мм мм мм мм мм мм мм ренная, мм по формуле (15) по формуле (16)

 

Часть 2. Влияние ширины полосы на уширение

Алюминиевые образцы шириной 5, 10, 20, 50 мм; длиной 60 мм и толщиной 2 мм прокатывают с одинаковым обжатием за проход Δh = 1 мм. Тщательно замеряют толщину и ширину образцов до и после прокатки. Во избежание искажения результатов образцы следует задавать в валки строго перпендикулярно. По формулам (14), (15) и (16) определяют расчетную ширину образца. Все результаты измерений заносят в табл. 3.2 и на милли­метровой бумаге строят график зависимости уширения Δb от отношения

b₀/h₀).

Таблица 3.2

№ образца	h0, мм	h1 , мм	Δh, мм	λ	b0, мм	b1 , мм	Δb, мм	b1 расчетная, мм
по формуле (15)	по формуле (16)

Из алюминия или свинца изготавливают две одинаковые треугольные пластины толщиной h₀=2 мм (рис. 15).

 

 

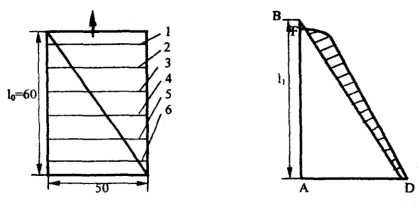
Рисунок 15 – Пластины для определения уширения в

зависимости от ширины

 

Тщательно замеряют толщину и ши­рину пластин в каждой точке 1, 2, 3, 4, 5, 6. Затем пластины складывают и одновременно прокатывают с обжатием Δh =1 мм. Тщательно замеряют толщину и ширину после прокатки в тех же точках. Исходя из закона по­стоянства объема и пренебрегая уширением, по формуле

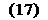l₁ = l₀ • λ

находят теоретическую длину полосы и строят теоретический треугольник АВС. По замеренным данным строят действительный треугольник AFD.

Заштрихованная площадь характеризует уширения. Все данные зано­сят в табл. 3.3.

Таблица 3.3

 

Точка	h0, мм	h1 , мм	Δh, мм	λ	b0, мм	b1 , мм	Δb, мм	b1 расчетная, мм
по формуле (15)	по формуле (16)

 

 

Часть 3. Влияние коэффициента трения на уширение

 

 

Два алюминиевых образца размером 2х40х60 мм прокатывают на стане с D_в = 100 мм с одинаковым обжатием Δh =1 мм: один на сухих (про­тертых ацетоном) валках, другой на смазанных машинным маслом. Тща­тельно замеряют толщину и ширину до и после прокатки. Проводят расчеты ширины по формулам (14) (15) и (16). Все данные заносят в табл. 3.4.

Таблица 3.4

Состояние валков	h0, мм	h1 , мм	Δh, мм	λ	b0, мм	b1 , мм	Δb, мм	b1 расчетная, мм
по формуле (15)	по формуле (16)
Со смазкой
Без смазки

 

Вывод_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________