Понятие случайного процесса. Функция распределения и плотность распределения значений в одном сечении случайного процесса. Многомерные распределения.
Сигналы в системах передачи информации и действующие в них помехи по своей природе являются случайными процессами(СП).Для их описания используется мат. аппарат теории вероятности и мат. статистики.
Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, то есть имеют вероятностный вид. Существует 2 основных класса случайных сигналов. Во-первых, это шумы — хаотически изменяющиеся во времени электромагнитные колебания, возникающие в разнообразных физических системах из-за беспорядочного движения носителей заряда. Во-вторых, случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
Случайный процесс (СП). Реализация СП
Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом. По определению, случайный процесс X(t) это функция особого вида, характеризующаяся тем, что значения, принимаемые ею в любой момент времени t, являются случайными величинами. До регистрации (до приёма) случайный сигнал следует рассматривать именно как случайный процесс, представляющий собой совокупность (ансамбль) функций времени Xj(t), подчиняющихся некоторой общей для них статистической закономерности. Одна из этих функций, ставшая полностью известной после приёма сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени.
На рис. изображены возможные реализации x1(t) и x2(t) случайного процесса X(t), являющиеся детерминированными функциями времени. Сам процесс можно трактовать как множество (в том числе и несчетное) подобных реализаций { xk(t) } с соответствующей вероятностной мерой.
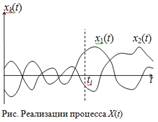Для анализа свойств и характеристик случайного процесса, а также различных его преобразований, необходимо задать математическую модель случайного процесса. Такая модель может представлять собой описание возможных реализаций случайного процесса в сочетании с указанием относительной частоты их появления. Для полного описания сечения СП необходимо указать закон распределения значений СП в этих сечениях. Они могут быть заданы в дифференциальной форме(через плотность вероятности) или интегральной форме(через функцию распределения).
В таблице, в порядке напоминания, приведены основные сведения об этих законах и их свойствах.
| Название и обозначение | Функция распределения F (x) | Плотность вероятности w (x) |
| Определение |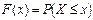 
| 
|
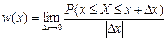
| Физическая размерность | безразмерная | размерность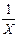 
|
| Взаимосвязь |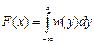 
| 
|
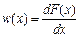
| Особенности функции | F (x 2)³ F (x 1) при x 2> x 1 (неубывающая) | w (x)³0 (неотрицательная) |
Расчет вероятности
| 
| 
|
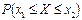
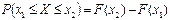
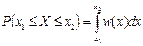
| Свойство нормировки |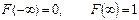 
| 
|
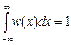
Пример
В качестве примера рассмотрим гармонический сигнал со случайной начальной фазой. Во многих практических задачах используется модель случайного процесса, реализации которого представляют собой гармонические колебания с известными (детерминированными) амплитудой и частотой, но случайной начальной фазой. Таким образом, реализация рассматриваемого случайного процесса может быть записана как:
x(t)=A*cos(ω0*t+φ)
где А амплитуда (детерминированная), ω0 — частота (детерминированная), и φ — случайная начальная фаза, которая в большинстве практически интересных случаев может считаться равномерно распределённой на интервале 0…2π, то есть имеющей следующую плотность вероятности:
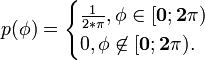
Графики нескольких реализаций данного случайного процесса, представляющие собой смещённые друг относительно друга по временной оси синусоиды, показаны на рис. Как видим, конкретный вид реализации процесса в данном случае определяется значением всего лишь одной случайной величины: начальной фазы. Случайные процессы, конкретный вид реализаций которых определяется значениями конечного числа параметров (случайных величин), называют квазидетерминированными случайными процессами.