Электрического слоя
Как было показано на прошлой лекции, возникновение заряда на поверхности частиц дисперсной фазы приводит к образованию двойного электрического слоя (рисунок 3).
Рис. 3. Возникновение двойного электрического слоя
на поверхности частиц
Вспомним, что, двойной электрический слой ( сокращенно ДЭС) – это система пространственно разделенных зарядов на границе раздела фаз. Заряды одного знака сосредоточены на поверхности частиц дисперсной фазы, а заряды противоположного знака сосредоточены в жидкости вблизи частиц. Необходимо отметить, что одна часть ионов прочно закреплена на поверхности частиц (химическими связями), а вторая часть (так называемые противоионы) – находятся в растворе и могут свободно перемещаться, отходя от частицы на достаточно большие расстояния. Именно строение ДЭС может помочь в объяснении причин влияния различных факторов на электрокинетический потенциал.
Были предложены различные теории строения двойного электрического слоя. Поскольку заряды на поверхности частицы жестко закреплены, то различие в строении ДЭС сводится к различию в строении слоя противоионов.
Исторически первой была теория Гельмгольца-Перрена.
Теория Гельмгольца-Перрена (1879г.).
Рассмотрим строение ДЭС по Гельмгольцу – Перрену.
В соответствии с этой теорией двойной электрический слой представляет собой плоский конденсатор. ДЭС рассматривается как плоскопараллельный. Это допущение приемлемо, поскольку толщина ДЭС намного меньше, чем радиус кривизны поверхности частицы.
Рассмотрим графическую иллюстрацию теории Гельмгольца – Перрена. На рисунке 4 жирной линией обозначена поверхность частицы дисперсной фазы. Одна обкладка – заряды на поверхности частицы (положительные, суммарный заряд +s), вторая обкладка – ряд противоионов (отрицательных) в растворе (суммарный заряд – s). Число положительных зарядов равно числу отрицательных. По оси х откладываем Х – расстояние от поверхности частицы. По оси у откладываем значение потенциала j в зависимости от расстояния от поверхности частицы. d – толщина слоя противоионов, равная радиусу гидратированного иона. Максимальное значение потенциала jо наблюдаетсяна поверхности частицы. В пределах толщины слоя противоионов d значение потенциала резко линейно падает до 0 в точке С. Это происходит потому, что противоионы полностью компенсируют заряд частицы и за пределами ДЭС суммарный заряд частицы равен 0. Как мы уже говорили, частицы дисперсной фазы при перемещении увлекают за собой часть жидкости. «А – В» – граница скольжения частицы относительно дисперсионной среды. График показывает, что в пределах границы скольжения коллоидная частица нейтральна (благодаря противоионам) и, следовательно, она не будет перемещаться в электрическом поле. Таким образом, теория Гельмгольца – Перрена не могла объяснить электрокинетические явления. К тому же, эта теория не учитывала теплового движения ионов в растворе.
   |
Рис. 4. Строение ДЭС по Гельмгольцу – Перрену
На смену теории Гельмгольца пришла теория Гуи-Чэпмена.
Теория Гуи-Чепмена (1910, 1913г.г.).
Теория Гуи-Чепмена – это теория ДЭС с диффузным слоем противоионов. Она устранила многие недостатки теории Гельмгольца – Перрена. С точки зрения этой теории на противоионы, находящиеся вблизи поверхности частицы, действуют две взаимно противоположные силы: электростатическое притяжение поверхности твердой фазы и тепловое движение, вследствие которого противоионы стремятся рассеяться во всем объеме жидкости (явление диффузии). Таким образом, слой противоионов приобретает диффузное строение.
Рассмотрим графическую иллюстрацию теории Гуи-Чепмена (рисунок 5).
    |
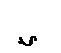Рис. 4. Строение ДЭС по Гуи -Чепмену
Поскольку противоионы рассредоточены от поверхности частицы вглубь раствора, то толщина слоя противоионов значительно увеличивается по сравнению с теорией Гельмгольца. Полная компенсация заряда поверхности происходит только на линии СД, и в точке Д величина потенциала становится равной 0. Падение потенциала происходит не по прямой, а по экспоненте. Надо отметить, что граница скольжения «А – В» в этом случае находится внутри диффузного слоя, на границе скольжения заряд частицы частично скомпенсирован (уменьшается), поэтому потенциал на этой границе, меньше термодинамического, но не равен 0. На границе скольжения при перемещении частицы возникает электрокинетический потенциал. Из графика видно, что величина z- потенциала составляет только часть термодинамического потенциала. Таким образом, эта теория могла объяснить электрокинетические явления и объясняла, почему электрокинетический потенциал меньше термодинамического.
Эта теория также могла объяснить влияние индифферентных электролитов на z- потенциал. В присутствии большого числа посторонних ионов толщина диффузного слоя уменьшается и соответственно падает значение электрокинетического потенциала (рисунок 6).
Рис. 6. Влияние электролитов на величину z- потенциала
При большой концентрации электролитов диффузный слой может уменьшиться до границы скольжения и z- потенциал станет равным 0 (кривая 3). Частицы дисперсной фазы перестанут перемещаться в электрическом поле. Такое состояние системы называется изоэлектрической точкой. Однако, эта теория не могла объяснить явление перезарядки поверхности, когда заряд частиц дисперсной фазы в присутствии ионов с высоким зарядом меняется на противоположный, и частицы в электрическом поле меняют свое направление.
Теория, которая вобрала в себя наиболее полезное из двух предшествующих теорий, была создана в 1924 году. Ее автором был Штерн.
Теория Штерна (1924г.).
Эта теория в настоящее время является общепринятой.
Рассмотрим графическую иллюстрацию этой теории (рисунок 7).
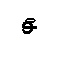
Согласно этой теории, слой противоионов состоит из двух частей. Одна часть противоионов примыкает к поверхности частицы и образует плотный адсорбционный слой толщиной d. Этот слой называют также слоем Гельмгольца (рисунок 7).
Рис. 7. Строение ДЭС по Штерну
Эти ионы прочно удерживаются на поверхности благодаря действию двух сил: электростатического притяжения и специфической адсорбции. Падение потенциала j d в этой части ДЭС происходит линейно.
Другая часть противоионов образует диффузный слой (слой Гуи). Толщина этого слоя l может быть значительной. В диффузной части потенциал снижается по экспоненте. Ионы диффузного слоя удерживаются частицей слабо и могут отходить от частицы на значительные расстояния. На границе скольжения «А – В» и в этом случае при перемещении частицы возникает электрокинетический потенциал z. Некоторые исследователи считают, что граница скольжения проходит между адсорбционным и диффузным слоем противоионов.
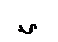
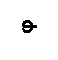
Теория Штерна смогла объяснить явление перезарядки поверхности. Это явление возникает при введении в коллоидный раствор ионов с высоким зарядом. Благодаря специфической адсорбции (а мы знаем правила ионной адсорбции: адсорбция возрастает при увеличении заряда) поверхность частицы меняет свой заряд на противоположный, поскольку суммарный заряд противоионов в адсорбционном слое больше заряда потенциалобразующих ионов (рисунок 8).
Рис. 8. Перезарядка поверхности
У поверхности частицы образуется новый диффузный слой противоионов, а электрокинетический потенциал сначала становится равным 0, а затем меняет знак на противоположный. Явление перезарядки поверхности можно наблюдать реально при изучении электрофореза. Например, частицы, которые перемещались в электрическом поле к катоду, при введении в раствор электролитов с многозарядными анионами вначале прекращают движение, а затем меняют направление перемещения на противоположное, то есть движутся к аноду.
Таким образом, теория Штерна смогла объяснить практически все электрические явления, наблюдаемые в гетерогенных системах, благодаря ей было установлено строение твердофазных частиц. Эта теория сыграла важную роль в изучении условий стабилизации и разрушения дисперсных систем.
ЗАКЛЮЧЕНИЕ
Подводим итоги изучения электрических свойств дисперсных систем. Эти свойства обусловлены возникновением двойного электрического слоя на поверхности частиц дисперсной фазы. Современная теория ДЭС – теорияШтерна – позволяет объяснить строение коллоидных мицелл и причины электрокинетических явлений – электрофореза, электроосмоса, потенциала течения и седиментации, которые возникают только при взаимном перемещении дисперсной фазы и дисперсионной среды.
Доктор технических наук, профессор
Т.Г. Дмитриенко
"___" ___________ 2013 г.