Далее, согласно (2.45), находится выражение инверсной расширенной амплитудно - фазовой характеристики объекта.

АНАЛИЗ И СИНТЕЗ СИСТЕМЫАВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

 

 

Методические указания к выполнению курсовой работы по дисциплине «Автоматическое регулирование»

 

 

Для специальностей: 5В071600 - Приборостроение

5В071800 - Электроэнергетика

 

 

Петропавловск

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РЕСПУБЛИКИ КАЗАХСТАН

 

Северо-Казахстанский государственный университет

им. М.Козыбаева

 

 

АНАЛИЗ И СИНТЕЗ СИСТЕМЫАВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

 

 

Методические указания к выполнению курсовой работы по дисциплине «Автоматическое регулирование»

 

 

Для специальностей: 5В071600 - Приборостроение

5В071800 - Электроэнергетика

 

Петропавловск

Рецензент:

Профессор кафедры ЭиР, д.т.н Кошеков К.Т.

 

 

Разработчики:

Зыкова Н.В., старший преподаватель кафедры ЭиР;

Пукема В.И., преподаватель кафедры ЭиР.

 

Методические указания к выполнению курсовой работы по дисциплине «Автоматическое регулирование» разработаны на кафедре «Энергетика и радиоэлектроника» и предназначены для студентов, обучающихся по специальностям 5В071600 «Приборостроение» и 5В071800 «Электроэнергетика».

Указания составлены на основании ГОСО РК, рабочих учебных планов и УМКД «Автоматическое регулирование».

В представленных указаниях рассмотрены вопросы исследования режимов системы автоматического управления, а также анализа и синтеза оптимальной системы «объект-регулятор».

 

Система менеджмента качества СКГУ им. М. Козыбаева сертифицирована на соответствие требованиям ИСО 9001:2008

 

Методические указания утверждены на заседании Учебно-методического совета инженерно-технического факультета

протокол № ___ «_____» ____________2014 г.

 

Председатель УМС ИТФ __________________ Р. Имамбаева

 

Методические указания рассмотрены и рекомендованы к утверждению на заседании кафедры «Энергетика и радиоэлектроника»

 

 

протокол № 4 «23» декабря 2013 г.

 

Заведующий кафедрой ЭиР __________________ К. Кошеков

 

 

СОДЕРЖАНИЕ

Стр.

Введение 5

1 Требования к содержанию курсовой работы 7

2 Порядок выполнения курсовой работы 8

2.1 Исследование режимов системы автоматического управления 8

2.1.1 Определение передаточной функции замкнутой системы 8

2.1.2 Построение логарифмической амплитудной частотной характеристики 11

2.1.3 Построение логарифмической фазовой частотной характеристики 14

2.1.4 Временные характеристики САУ 16

2.1.5 Исследование устойчивости САУ 20

2.1.6 Варианты заданий для выполнения первой части курсовой работы 41

2.2 Синтез системы «объект-регулятор» 44

2.2.1 Анализ и синтез оптимальной системы «объект-регулятор» 44

2.2.2 Определение оптимальных параметров настройки П,

ПИ, ПИД – регуляторов 48

2.2.3 Построение переходных характеристик синтезированной системы «объект-регулятор» в среде MATLAB 53

2.2.4 Реализация синтезированной системы на реальных электрических элементах в программах электронного моделирования 56

2.2.5 Варианты заданий для выполнения второй части курсовой работы 64

2.2.6 Пример выполнения второй части курсовой работы 71

3 Требования к оформлению курсовой работы 84

4 Критерии оценивания защиты курсовой работы 87

Рекомендуемая литература 88

 

Введение

 

Целью курсовой работы по дисциплине «Основы автоматики» является закрепление теоретических знаний и выработка практических навыков по проектированию промышленных автоматических систем регулирования.

Как известно, при исследовании различных свойств автоматических систем используют два подхода: экспериментальный и теоретический. В связи с этим курсовая работа разбита на две части, расчет характеристик САУ и моделирование системы.

В самом общем виде порядок исследования систем автоматического управления (САУ) включает математическое описание системы, исследование ее установившихся режимов и исследование переходных режимов.

Математическое описание системы, т.е. получение ее математической модели, начинается с разбиения ее на звенья и описания этих звеньев. Последнее может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих ту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения системы в целом, на основании которых и исследуется система.

При выполнении первой части курсовой работы перед студентом ставятся следующие задачи и цели:

1. Закрепление и более глубокое усвоение определенного объема теоретических знаний, включающего ниже перечисленные вопросы:

– методы построения и преобразования структурных схем системы автоматического управления (САУ);

– передаточные функции типовых звеньев САУ;

– основные критерии устойчивости переходных процессов САУ.

2. Приобретение навыков, освоение методов технического расчета и проектирования при составлении математического описания и анализе устойчивости САУ.

3. Развитие самостоятельности при выборе методов расчета и инициативы при решении конкретных задач.

Основной целью второй части курсовой работы является подготовка специалистов к участию в разработке и проектировании новых промышленных приборов и систем, создании математического обеспечения и моделей для автоматизированных систем управления производством, т.е. формирование знаний и навыков у студентов в области таких вопросов как промышленные приборы и преобразователи, автоматические регуляторы.

Так как в последнее время кафедра интенсивно оснащается новым учебно-лабораторным оборудованием, и в образовательный процесс активно внедряются компьютерные технологии, появилась возможность использования инновационных технологий для проверки теоретических расчетов и с целью построения различных графиков и характеристик исследуемых процессов.

В связи с этим в качестве базового направления выбрана задача анализа и синтеза оптимальной одноконтурной САУ и определение параметров оптимальной настройки автоматических регуляторов. Для расчета и проектирования данной системы необходим определенный объем знаний по теории автоматического управления (теория линейных систем, критерии устойчивости и качества переходных процессов автоматических систем и т.д.) и опыт работы с программой математического моделирования MATLAB.

Таким образом, вторая часть курсовой работы включает в себя следующие задачи:

- определение передаточной функции объекта управления;

- расчет параметров регуляторов и выбор оптимального регулятора;

- синтез полученной системы «регулятор-объект» в среде MATLAB;

- построение переходной характеристики с целью определения показателей качества системы.

1 Требования к содержанию курсовой работы

 

В соответствии с рабочей программой дисциплины, курсовая работа должна содержать следующие разделы:

- краткий обзор теории автоматических регуляторов;

- краткая характеристика системы принятой в качестве цели исследования и области, к которой относится исследуемая система;

- определение передаточной функции замкнутой системы (первая часть курсовой работы; схема САУ приведена на рисунке 2.14; исходные данные в таблице 2.4);

- определение и построение логарифмической амплитудной частотной характеристики;

- определение и построение логарифмической фазовой частотной характеристики;

- определение и построение временных характеристик (переходного процесса) САУ;

- исследование устойчивости САУ;

- анализ и синтез системы «объект-регулятор» с выбором оптимального регулятора (вторая часть курсовой работы; схема САУ приведена на рисунке 2.15; исходные данные в таблице 2.5);

- получение переходных характеристик синтезированной системы в среде MATLAB;

- реализация синтезированной системы на реальных электрических элементах в программах электронного моделирования (EWB, Multisim, Micro-Cap, PSpice) с построением кривой переходного процесса.

 

2 Порядок выполнения курсовой работы

 

2.1 Исследование режимов системы автоматического управления

 

2.1.1 Определение передаточной функции замкнутой системы

Рассмотрим получение передаточной функции одномерной системы на примере схемы, изображенной на рисунке 2.1.

Рисунок 2.1. Одноконтурная САУ

 

На рисунке 2.1 приняты следующие условные обозначения:

КУ – корректирующее устройство;

ОИ – объект исследования;

РЭ – регистрирующий элемент.

Уравнение усилителя:

 

у₁=(k₁ /р) ∙Δx

Уравнение объекта исследования:

 

(1+Т₁р)∙у₂=k₂ ∙у₁

Уравнение регистрирующего элемента:

 

х_о.с.=k_3∙у₂

Для нахождения общей передаточной функции системы необходимо знать передаточную функцию каждого входящего в нее элемента.

Передаточная функция динамического звена определяется отношением выходной реакции звена к внешнему воздействию. Таким образом, используя заданные уравнения структурных элементов системы, получим следующие выражения:

Передаточная функция КУ соответствует передаточной функции интегрирующего звена:

 

. (2.1)

Передаточная функция ОИ соответствует передаточной функции апериодического звена:

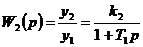. (2.2)

Передаточная функция РЭ соответствует передаточной функции пропорционального звена:

 

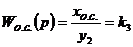. (2.3)

 

Так как рассматриваемая система (рисунок 2.1) содержит обратную связь, то общая передаточная функция будет рассчитываться:

 

. (2.4)

 

Передаточная функция прямой цепи определяется как функция цепочки последовательно соединенных звеньев. Согласно правилу она равна произведению передаточных функций звеньев, то есть:

 

. (2.5)

 

Подставив значение передаточных функций из (2.1) и (2.2) в выражение (2.5) получим:

. (2.6)

 

Итак, формула для определения общей передаточной функции (2.4) после необходимых преобразований запишется следующим образом:

 

. (2.7)

 

В знаменателе знак «+» соответствует отрицательной обратной связи, а знак «–» –отрицательной. Допустим в данном случае обратная связь отрицательная. Для дальнейшего исследования САУ (рисунок 2.1) зададим числовые значения параметров: Т₁=0,4, k₁=10, k₂=6, k₃=4.

Подставим в (2.7) заданные значения, получим:

 

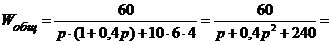(2.8)

.

 

Теперь необходимо узнать, к какому типу элементарных звеньев относится полученная передаточная функция. В зависимости от значения коэффициента затухания ξ=Т₂/2Т₁ звено может быть колебательным (0< ξ <1), консервативным (ξ =0) и апериодическим второго порядка (ξ ≥1). Итак, ξ =0,004/2∙ 0,04=0,05, следовательно, звено колебательное.

 

 

2.1.2 Построение логарифмической амплитудной частотной характеристики

Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе. При гармоническом воздействии в устойчивых системах, после окончания переходного процесса, выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. И, следовательно, амплитудная частотная характеристика показывает изменение отношения амплитуд, а фазовая частотная характеристика – сдвиг фазы выходной величины относительно входной в зависимости от частоты входного гармонического воздействия.

Уравнение асимптотической логарифмической амплитудной частотной характеристики (ЛАЧХ) для колебательного звена имеет вид:

 

L(ω) ≈ (2.9)

 

 

где ω₁=1/ T₁, ω₁ – сопрягающая частота, точка пересечения асимптот. Первая асимптота, при ω<ω₁, параллельна оси частот, а вторая, при ω≥ ω₁, имеет наклон – 40 дБ/дек.

Определим начальную точку первой асимптоты: 20lgk= 20lg0,25= –12. Сопрягающая частота ω₁=1/ T₁=1/0,04=25; lg (ω₁)=1,4. Итак, из точки со значением –12 проводим первую асимптоту – прямую линию, параллельную оси частот. В точке ω₁=1,4 происходит излом логарифмической характеристики, начинается вторая асимптота с наклоном – 40 дБ/дек (рисунок 2.2). Необходимо помнить, что на оси абсцисс указываются либо прямо значения lg ω, либо, что практически более удобно, значения самой частоты ω. В первом случае единицей приращения lg ω является декада, соответствующая изменению частоты в 10 раз. По оси ординат откладывается десятичный логарифм коэффициента мощности сигнала, единицей измерения которого является децибел.

Рисунок 2.2. Амплитудная частотная характеристика

колебательного звена

 

Рассмотрим построение ЛАЧХ в случае апериодического звена второго порядка. Это звено не относится к числу элементарных звеньев, его можно представить как последовательное соединение двух апериодических звеньев первого порядка.

Для этого необходимо найти корни характеристического уравнения передаточной функции звена Т₃, Т₄:

 

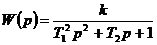, (2.10)

 

Тогда передаточная функция апериодического звена второго порядка запишется следующим образом:

 

. (2.11)

 

Уравнение асимптотической ЛАЧХ для апериодического звена второго порядка имеет вид:

 

L(ω)≈ (2.12)

 

Первая асимптота начинается в точке 20lgk и продолжается до точки сопрягающей частоты ω₁=1/ T₃ – начало второй асимптоты, которая откладывается с наклоном – 20дБ/дек. Третья асимптота начинается в точке сопрягающей частоты ω₂=1/ T₃ и имеет наклон уже – 40дБ/дек. В результате получим характеристику, изображенную на рисунке 2.3.

 

		lg ω

 

 

Рисунок 2.3. Амплитудная частотная характеристика апериодического звена второго порядка

 

 

2.1.3 Построение логарифмической фазовой частотной характеристики

 

Логарифмическая фазовая частотная характеристика (ЛФЧХ) колебательного звена изменяется монотонно от 0 до –π и выражается формулой:

 

φ(ω)=

(2.13)

 

ЛФЧХ при ω→0 асимптотически стремится к оси частот, а при ω→∞ – к прямой φ= =–π.

Рисунок 2.4. Фазовая частотная характеристика

колебательного звена

 

Для построения характеристики (рисунок 2.4) воспользуемся таблицей 2.1, в которую занесены значения частоты ω и рассчитанные с помощью формулы (2.13) соответствующие значения фазы φ. При этом постоянные времени остаются прежними, как и в пунктах 2.1.1, 2.1.2, т.е. Т₁=0,04, Т₂=0,004.

 

 

Таблица 2.1

ω
lg ω		1,3	1,34	1,38	1,48	1,69
φ(ω)	-3	-12,5	-20	-45	-75	-86	-89

 

Рассмотрим построение ЛФЧХ для апериодического звена второго порядка. Так как это звено можно представить в виде двух апериодических звеньев первого порядка, соединенных последовательно, то общая ЛФЧХ φ(ω) будет представлять собой сумму фазовых частотных характеристик апериодических звеньев первого порядка.

 

φ(ω) = -arctg ωT₃ - arctg ωT₄

ЛФЧХ в этом случае при ω→0 асимптотически стремится к оси частот, а при ω→∞ – к прямой φ= –2π.

 

2.1.4 Временные характеристики САУ

 

Важной характеристикой автоматических систем (звеньев) является переходные и импульсные переходные функции и их графики – временные характеристики.

Переходной функцией системы (звена) называют функцию, описывающую изменение выходной величины системы (звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Другими словами, переходная функция h(t) есть функция, описывающая реакцию системы (звена) на единичное ступенчатое воздействие при нулевых начальных условиях.

Переходная функция колебательного звена равна:

 

(2.14)

где , .

 

Подставив заданные параметры колебательного звена k=0,25, Т₁=0,04, Т₂=0,004, получим следующее выражение:

 

h(t)=0,25[1-2,7^-1,25t ∙sin(25t-87)].

 

Данная функция h(t) и есть переходная характеристика исследуемой автоматической системы (рисунок 2.1), для построения графика этой характеристики (рисунок 2.5) понадобится таблица 2.2.

 

Таблица 2.2

t		0,01	0,06	0,5		1,5
h(t)		0,49	0,47	0,37	0,31	0,27	0,25	0,249	0,248	0,249

 

При построении графика (рисунок 2.6) переходной функции апериодического звена второго порядка используется зависимость

 

, (2.15)

 

где Т₃ и Т₄ корни характерестического уравнения передаточной функции (2.10).

Импульсной переходной, или весовой, функцией системы (звена) называют функцию, описывающую реакцию системы (звена) на единичное импульсное воздействие при нулевых начальных условиях.

Весовая и переходная функции связаны между собой следующим образом:

 

ω (t)=h(t)' (2.16)

Рисунок 2.5. Переходная характеристика колебательного звена

Рисунок 2.6. Переходная характеристика апериодического звена второго порядка

Таким образом, дифференцируя выражение (2.14), можно найти весовую функцию колебательного звена.

 

. (2.17)

 

Для построения импульсной характеристики (рисунок 2.7) воспользуемся таблицей 2.3.

 

Таблица 2.3

t	0,1	0,5		1,2	1,5
ω(t)	0,01	0,03	0,032	0,030	0,026
t	1,7		2,2	2,5
ω(t)	0,022	0,018	0,014	0,01	0,006

 

Рисунок 2.7. Весовая характеристика колебательного звена

 

Если исследуемое звено является апериодическим второго порядка, то импульсная характеристика (рисунок 2.8) будет соответствовать выражению:

, (2.18)

 

где Т₃ и Т₄ корни характерестического уравнения передаточной функции (2.10).

 

 

 

 

Рисунок 2.8. Весовая характеристика апериодического звена второго порядка

 

 

2.1.5 Исследование устойчивости САУ

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

На рисунке 2.9 показаны типичные кривые переходных процессов в неустойчивой (рисунок 2.9. а) и устойчивой (рисунок 2.9. б) системах. Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (кривая 1 на рисунке 2.9. а) или колебательным (кривая 2 на рисунке 2.9. а).

Рисунок 2.9. К понятию устойчивости системы

		t

Апериодический расходящийся процесс может, например, возникнуть в САУ, если в ее управляющем устройстве ошибочно переключить полярность воздействия на объект, в результате чего управляющее устройство будет осуществлять не отрицательную, а положительную обратную связь вокруг объекта. При этом управляющее устройство будет не устранять отклонение х, а действовать в обратном направлении, вызывая лавинообразное его изменение.

Колебательный расходящийся процесс, как будет показано далее, может наступить, например, при неограниченном увеличении коэффициента передачи системы, вследствие чего управляющее устройство станет излишне энергично воздействовать па объект, стремясь ликвидировать первоначально возникшие отклонения х. В этом случае при каждом очередном возврате х к нулю под действием управляющего устройства кривая х будет пересекать ось абсцисс все с большей скоростью и процесс в целом будет расходящимся.

В случае устойчивой системы (рисунок 2.9. б) переходный процесс, вызванный каким-либо воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2), и система вновь возвращается в установившееся состояние.

Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.

Приведенное понятие устойчивости определяет устойчивость установившегося режима системы. Однако система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. С учетом таких условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если ее выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений.

Нетрудно показать, что если переходный процесс в системе является затухающим, то система будет удовлетворять и последнему определению.

Рассмотрим, от чего зависит устойчивость системы, чем она определяется. Обратимся для этого к уравнению динамики системы:

 

x = W_з(s)f,

 

где W_з(s) = W_xf(s)/(1 + W(s));

W(s) = R(s)/Q(s); W_xf(s) = R_xf(s)/Q_xf(s).

Освободившись от дробей в числителе и знаменателе передаточной функции, можно представить ее так:

 

W_з = M(s)/D(s)

 

и соответственно перейти к обычной форме записи в виде дифференциального уравнения:

 

D(s)x = M(s)f. (2.19)

 

Решение этого линейного неоднородного уравнения в общем виде состоит, как известно, из двух составляющих:

 

x(t) = x_уст(t) + x_п(t). (2.20)

 

Здесь x_уст(t) – частное решение неоднородного уравнения (2.19) с правой частью, описывающее вынужденный режим системы, устанавливающийся по окончании переходного процесса; такие режимы были рассмотрены; x(t) — общее решение однородного уравнения:

 

D(s)x = 0,

 

описывающее переходный процесс в системе, вызванный данным возмущением.

Как показано выше, система будет устойчива, если переходные процессы x_п(t), вызванные любыми возмущениями, будут затухающими, т. е. если с течением времени x (t) будет стремиться к нулю.

Решение x_п(t) однородного дифференциального уравнения, как известно, имеет вид:

 

(2.21)

Здесь C_i – постоянные интегрирования, определяющиеся начальными условиями и возмущенном, l_i – корни характеристического уравнения

 

D(l) = 0 (2.22)

 

где полином D(l), называемый характеристическим, есть левая часть уравнения (2.19) динамики системы после замены оператора дифференцирования s на комплексную переменную l.

Полином D (l) является знаменателем передаточной функции W_з (s) системы после освобождения в нем от дроби и замены s на l, т. е.

 

D(l) = R(l) + Q(l), (2.23)

 

где R(l) и Q (l) — числитель и знаменатель передаточной функции W(s) разомкнутой системы при замене р на l.

Таким образом, переходный процесс x_п(t) представляет собой сумму составляющих, число которых определяется числом корней l_i характеристического уравнения (2.22), т. е. порядком уравнения системы.

В общем случае корни l_i являются комплексными. При этом они образуют пары сопряженных корней:

 

l_{i,i + 1} = a_i ± jb_i,

 

где a_i может быть положительной или отрицательной величиной. Каждая такая пара корней дает в выражении (2.21) составляющую переходного процесса, равную:

 

 

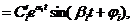
где C'_i и j_i определяются через С_i и C_{i +1}.

Как видим, эта составляющая представляет собой синусоиду с амплитудой, изменяющейся во времени по экспоненте. При этом, если a_i< 0, эта составляющая будет затухать. Наоборот, при a_i > 0 получатся расходящиеся колебания. Если a_i = 0, что соответствует паре мнимых корней, будут незатухающие синусоидальные колебания.

Таким образом, условием затухания данной составляющей переходного процесса является отрицательность действительной части a_i, соответствующей пары сопряженных корней характеристического уравнения. В частном случае, когда, b_i = 0 имеем действительный корень l_i = a_i. Соответствующая ему составляющая переходного процесса С_ie^at представляет собой экспоненту, которая будет затухать или увеличиваться тоже в зависимости от знака a_i.

 

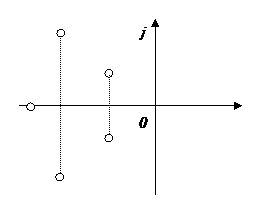Рисунок 2.10. Корни характеристического уравнения системы

на комплексной плоскости

 

Итак, в общем случае переходный процесс в системе состоит из колебательных и апериодических составляющих. Каждая колебательная составляющая обязана своим появлением паре комплексных сопряжении корней, а каждая апериодическая — действительному корню. Отсюда следует, что общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательность действительных частей всех корней характеристического уравнения системы, т. е. всех полюсов (нулей знаменателя) передаточной функции системы.

Если хотя бы один корень имеет положительную действительную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчивой. Наличие пары сопряженных чисто мнимых корней l_{i,i + 1} = ± jβ_i даст незатухающую гармоническую составляющую переходного процесса. При этом в системе установятся незатухающие колебания с частотой, равной b_i. Этот случай является граничным между устойчивостью и неустойчивостью – система при этом находится на границе устойчивости. Такая система, очевидно, также неработоспособна, как и неустойчивая.

Если изобразить корни характеристического уравнения системы точками на комплексной плоскости (рисунок 2.10), то найденное выше общее условие устойчивости линейной системы можно сформулировать еще так: условием устойчивости системы является расположение всех корней характеристического уравнения, т. е. полюсов передаточной функции системы, в левой комплексной полуплоскости или, короче, все они должны быть левыми.

Наличие корня на мнимой оси означает, что система находится на границе устойчивости.

Для суждения об устойчивости системы практически не требуется находить корней ее характеристического уравнения в связи с тем, что разработаны косвенные признаки, по которым можно судить о знаках действительных частей этих корней и тем самым об устойчивости системы, не решая самого характеристического уравнения. Эти косвенные признаки называются критериями устойчивости.

Существуют три основных критерия устойчивости: критерий Рауса – Гурвица, критерий Михайлова и критерий Найквиста. Рассмотрим их последовательно.

Критерий устойчивости Рауса – Гурвица.

Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. В разной форме этот критерий был предложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем в конце прошлого века. Приведем без доказательства этот критерий в форме Гурвица.

Возьмем характеристический полином, определяющий левую часть уравнения (2.19) системы,

 

D(l) = a₀lⁿ + a₁l^{n – 1} + … + a_n-1l + a_n, (2.24)

 

где полагаем a₀ > 0, что всегда можно обеспечить умножением при необходимости полинома на – 1. Составим из коэффициентов этого полинома определитель

 

. (2.25)

 

Этот определитель называется определителем Гурвица. Он имеет п строк и п столбцов. Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется до положенного числа п элементов нулями. Вторая строка включает все четные коэффициенты и тоже заканчивается нулями. Третья строка получается из первой, а четвертая — из второй сдвигом вправо на один элемент. На освободившееся при этом слева место ставится нуль. Аналогично сдвигом вправо на элемент получаются все последующие нечетные и четные строки из предыдущих одноименных строк.

В результате в главной диагонали определителя оказываются последовательно все коэффициенты, кроме а₀.

Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.

Развернем критерий Гурвица для нескольких конкретных значений п.

Для n =1

D(l) = a₀l + a₁

 

и условия устойчивости сводятся к неравенствам:

 

a₀ > 0; a₁ >0.

 

Отсюда, например, звено первого порядка с передаточной функцией k/(Ts + 1) является устойчивым, а звено с передаточной функцией k/(Ts – 1) неустойчивым.

Для n = 2

 

Условия устойчивости:

 

a₀ > 0; a₁ > 0; a₂ > 0

(к последнему неравенству сводится неравенство D₂ > 0, если учесть предыдущее неравенство а₁ > 0).

Например, звено с передаточной функцией k/(T²₁s+T₂s+1) устойчиво, если перед всеми членами в знаменателе стоит знак плюс.

Для n = 3

 

 

Условия устойчивости:

 

 

Последнее неравенство с учетом предпоследнего условия D₂ > 0 сводится к требованию а₃ > 0. Таким образом, в целом эти условия устойчивости заключаются в положительности всех коэффициентов и предпоследнего минора D₂. (Необходимость положительности а₂ вытекает из условия D₂ > 0 и положитель­ности всех остальных коэффициентов.)

Для n = 4

Условия устойчивости:

 

a₀ >0; a₁ > 0; ∆₂ = a₁a₂ – a₀a₃ > 0

∆₄ = a₄ ∆ ₃ > 0.

Легко видеть, что условия устойчивости опять сводятся к требованию положительности всех коэффициентов и предпоследнего минора ∆₃.

Для n = 5.

 

D(l) = a₀l⁵ + a₁l⁴ + … + a₄l + a₅.

Условия устойчивости, если действовать аналогично, сведутся к положительности всех коэффициентов и двух миноров: ∆ ₂ и предпоследнего ∆ ₄.

Можно показать в общем случае системы п- го порядка, что в условия устойчивости в качестве их части входит требование положительности всех коэффициентов уравнения. Анализ устойчивости надо начинать с проверки этого простого необходимого, но недостаточного условия устойчивости. При его невыполнении, естественно, отпадает надобность в составлении и проверке остальных неравенств.

Условия устойчивости, получаемые из критерия Рауса – Гурвица, как видно из изложенного, усложняются с ростом порядка системы. При этом для систем достаточно высокого порядка оказывается затруднительным выяснять влияние на устойчивость системы значений отдельных параметров звеньев, входящих в состав коэффициентов уравнения. Это связано с тем, что, как правило, одни и те же параметры одновременно входят в несколько коэффициентов уравнения системы. Поэтому критерий Рауса – Гурвица применяют только для систем невысокого порядка и, прежде всего, для анализа устойчивости, когда надо определить, устойчива ли система при известных значениях всех ее параметров. При решении задачи синтеза системы, когда требуется выбрать значения отдельных параметров системы, критерий Рауса – Гурвица становится неудобным уже для систем выше четвертого порядка.

Рассмотрим в качестве примера систему третьего порядка, состоящую из трех статических звеньев первого порядка. Передаточная функция этой системы имеет вид:

 

W(p) = k₁k₂k₃/(T₁p + 1)(T₂p + 1)(T₃p + 1). (2.26)

 

В этом случае

 

D(l) = R(l) + Q(l) = k₁k₂k₃ + (T₁p + 1)(T₂p + 1)(T₃p + 1),

т. е.

 

 

Здесь

 

a₀ = T₁T₂T₃; a₁ = T₁T₂ + T₂T₃ + T