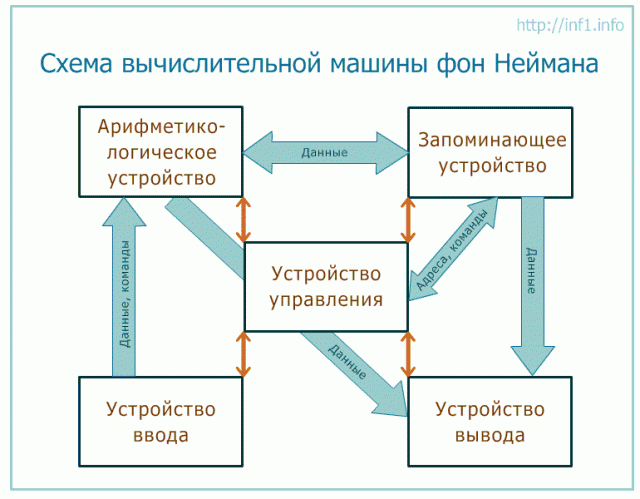
Машина фон Неймана состоит из запоминающего устройства (памяти) - ЗУ, арифметико-логического устройства - АЛУ, устройства управления – УУ, а также устройств ввода и вывода.
Программы и данные вводятся в память из устройства ввода через арифметико-логическое устройство. Все команды программы записываются в соседние ячейки памяти, а данные для обработки могут содержаться в произвольных ячейках. У любой программы последняя команда должна быть командой завершения работы.
Команда состоит из указания, какую операцию следует выполнить (из возможных операций на данном «железе») и адресов ячеек памяти, где хранятся данные, над которыми следует выполнить указанную операцию, а также адреса ячейки, куда следует записать результат (если его требуется сохранить в ЗУ).
Арифметико-логическое устройство выполняет указанные командами операции над указанными данными.
Из арифметико-логического устройства результаты выводятся в память или устройство вывода. Принципиальное различие между ЗУ и устройством вывода заключается в том, что в ЗУ данные хранятся в виде, удобном для обработки компьютером, а на устройства вывода (принтер, монитор и др.) поступают так, как удобно человеку.
УУ управляет всеми частями компьютера. От управляющего устройства на другие устройства поступают сигналы «что делать», а от других устройств УУ получает информацию об их состоянии.
Управляющее устройство содержит специальный регистр (ячейку), который называется «счетчик команд». После загрузки программы и данных в память в счетчик команд записывается адрес первой команды программы. УУ считывает из памяти содержимое ячейки памяти, адрес которой находится в счетчике команд, и помещает его в специальное устройство — «Регистр команд». УУ определяет операцию команды, «отмечает» в памяти данные, адреса которых указаны в команде, и контролирует выполнение команды. Операцию выполняет АЛУ или аппаратные средства компьютера.
В результате выполнения любой команды счетчик команд изменяется на единицу и, следовательно, указывает на следующую команду программы. Когда требуется выполнить команду, не следующую по порядку за текущей, а отстоящую от данной на какое-то количество адресов, то специальная команда перехода содержит адрес ячейки, куда требуется передать управление.
22. Представление числовой информации в ЭВМ. Двоичная арифметика.
Представление целых положительных чисел последовательностью нулей и единиц:
Двоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
Десятичная система:
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10

Перевод целых чисел из десятичной системы счисления в двоичную: 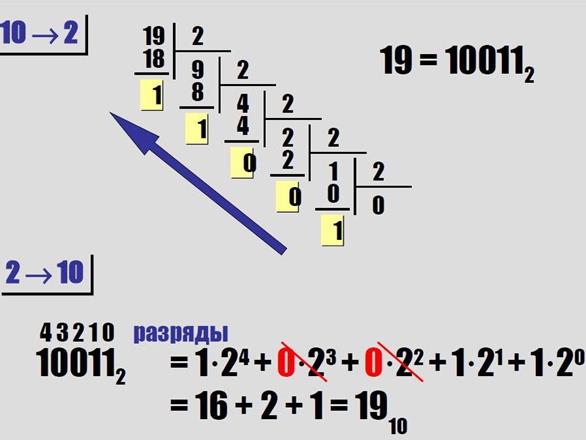
Перевод дробных чисел из десятичной системы счисления в двоичную: Тут подробно показано как переводить дробь в двоичную сис-му:
(https://www.youtube.com/watch?feature=player_embedded&v=eptc-hV66f0#!)
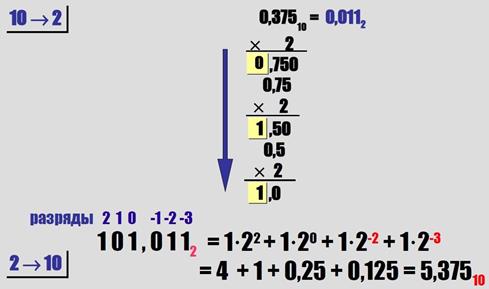
Многие дробные числа нельзя представить в виде конечных двоичных дробей.
Для их точного хранения требуется бесконечное число разрядов. Большинство дробных чисел хранится в памяти с ошибкой.
Хранение числовых величин:

Арифметические операции:
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0х0=0 0х1=0 1х0=0 1х1=1 |
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Пример. Выполнить сложение двоичных чисел:
а) X=1101, Y=101;

Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;
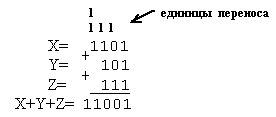
Результат 1101+101+111=11001.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.
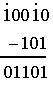
Результат 10010 - 101=1101.
Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.
Пример
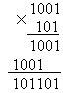
Результат 1001х101=101101.
Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.
Пример.
