Последовательные и параллельные схемы реакторов

Для проточных реакторов идеального смешения, соединенных в каскад (К-РИС-Н), используют графический и аналитический методы расчета

Графический метод расчета. Этот метод прост и позволяет рассчитать каскад реакторов идеального смешения непрерывного действия для реакции любого порядка.

В основе расчета лежит уравнение (5)

, (19)

где с_{i, m-1} - концентрация реагентана входе в m-ый реактор;

с_{i, m}- концентрация реагента на выходе из m-го реактора.

Из уравнения (19) находим, что

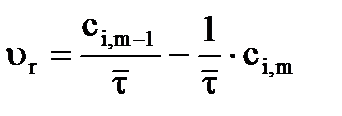(20)

Как видно из уравнения (20), для m-го реактора зависимость скорости реакции от концентрации изображается в виде прямой с углом наклона, для которого (рис. 3). С другой стороны, скорость реакции описывается уравнением

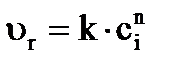, (21)

которое на графике в координатах от представляет собой при n>1 экспоненту, а при n = 1 прямую линию. Точка пересечения линии уравнений (19) и (20) характеризует концентрациюреагента в m-ом реакторе.

Для расчета К-РИС-Н графическим методом необходимо:

1. Вначале построить график по уравнению (19) зависимости u_r от С_i.

2. Затем из точки, лежащей на оси абсцисс, для которой провести прямую с тангенсом угла наклона, равным 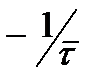до пересечения с кривой (прямой) в точке М: .

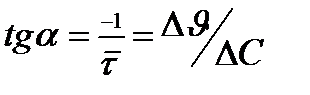3. Опустив перпендикуляр из точки пересечения М на ось абсцисс, получают значение концентрации реагента на выходе из первого реактора. Эта же концентрация является исходной для второго реактора.

4.

υr

Для нахождения концентрации во втором реакторе операцию повторяют, взяв за исходную точку , и т. д. до тех пор, пока в последнем реакторе не будет достигнута заданная концентрация . При этом число ступеней и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения.

М

Е

Д

при n>1

υr=k·Cin

α

сi,2

сi,3

сi

 

 

 

Рис. 3. Графический метод расчета каскада реакторов идеального смешения

Аналитический метод расчета. Аналитический метод расчета используется только для химических реакций первого порядка.

Предположим, что в каскаде реакторов протекает изотермическая реакция первого порядка при постоянной массовой плотности. Объемы реакторов в каскаде одинаковы. Тогда концентрация реагента А на выходе из первого реактора выражается формулой

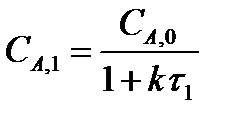(22).

Концентрация на выходе из второго реактора представлена следующей формулой

(23).

Таким образом, для концентрации на выходе из последнего реактора каскада С_Am будет иметь следующее рекуррентное выражение:

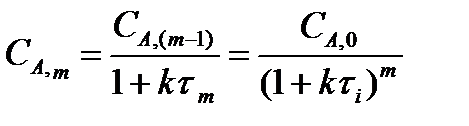(24).

Когда реакционные объемы равны, уравнение принимает следующий вид:

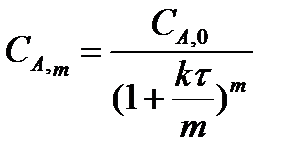(25).

Здесь величина τ определяется по полному объему всех реакторов.

Если в каскаде реакторов одинакового объема протекает изотермическая реакция второго порядка, то воспользовавшись теми же соотношениями, что и для реакции первого порядка, можно получить следующее выражение:

(26).

Уравнения (24) - (26) позволяют определить объемы каскада реакторов или их число, если известны остальные параметры процесса.

Отметим, что в случае расчета реакторов соединенных параллельно, необходимо учитывать расход исходного сырья на каждой из ветвей соединения. Расчетные параметры определяют суммированием уравнений, составленных для каждой ветви. Рассмотрим некоторые примеры расчета различных типов реакторов, соединенных последовательно, параллельно и смешанно.

Пример 9.

Процесс описывается реакцией типа А → 2R и осуществляется в установке из трех реакторов смешения (рис.4) Время пребывания в обоих ветвях установки одинаковое. Определить производительность по продукту R.

Дано:

объемный расход исходного вещества G₀ =18 м³/ч;

начальная концентрация исходного вещества С_А0= 2,6 кмоль/ м³;

константа скорости реакции k= 0.02 с ^-1;

Объемы реакторов V_p1=0,2 м³, V_p1=0,2м³, V_p1=0,6 м³

G₀₁

V_p1 V_p2

G₀

V_p3

G₀₂

Рис.4. Смешанная схема соединения реакторов

 

Решение.

Производительность установки по продукту R складывается из производительностей верхней и нижней ветвей:

П_R = П_R1+ П_R2 = 2G₀₁ С_А,0 х_А1 + 2G₀₂ С_А,0 х_А2.

По условию задачи время пребывания в обеих ветвях установки одинаково, тогда:

τ_в= τ₁ + τ₂ или , но τ_в= τ₂; и можно записать:

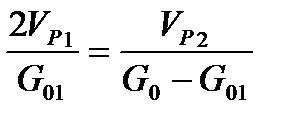или , или .

Решая это уравнение относительно V_01, получаем:

G₀₁ = 2 л/с =7,2м3/ч, G₀₂ = 3 л/с = 10,8м3/ч.

Определяем время τ₁ = τ₂ =200/2=100 с; τ_н =600/3=200с.

Находим концентрацию вещества А и степень превращения на выходе из верхних и нижних ветвей установки:

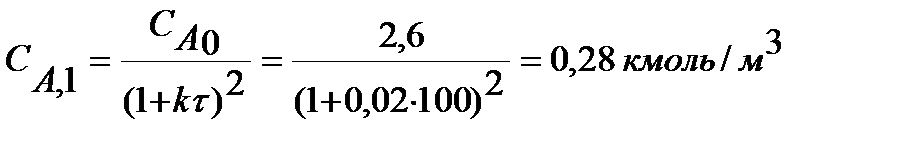
Определяем степени превращения и концентрации на выходе:

;

;

.

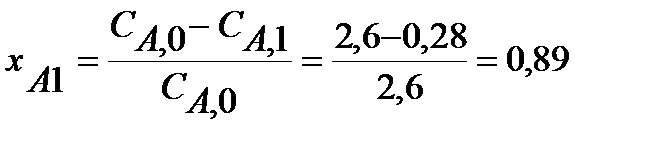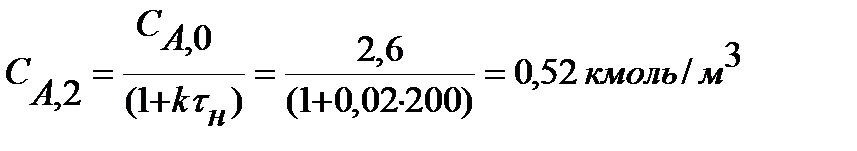Определяем производительность по продукту R:

П_R = 2G₀₁ С_А0 х_А1 + 2G₀₂ С_А0 х_А2 =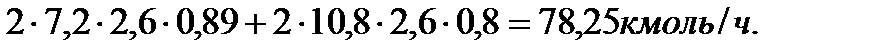

Пример 10.

Реакция проводится в параллельной схеме соединения реакторов РИС-Н и РИВ (рис.5.). Исходный поток по реакторам разделяется поровну. Определить объемные расходы, подаваемые в каждый реактор, и производительность по продукту R.

Дано:

Схема реакции А → R

объемный расход исходного вещества G₀ =720 л/мин;

начальная концентрация исходного вещества С_А0= 3 моль/л;

константа скорости реакции k= 0,25 с ^-1;

объемы реакторов V_p1=0,08 м³, V_p2=0,05м³.1

G₀₁

V_p1

G₀

 

G₀₂ V_p2

Рис.5. Схема параллельного соединения реакторов

Решение.

По условию задачи G₀₁ = G₀ = 720/2 = 360 л/мин = 6 л/с.

Определяем время пребывания в реакторе смешения и реакторе вытеснения:

; .

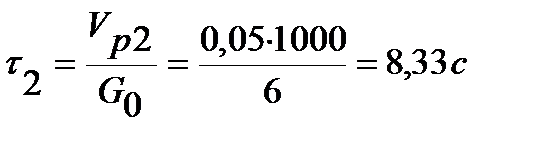Находим степень превращения вещества А в реакторах:

; .

Рассчитаем производительность по продукту R:

П_R = G₀₁ С_А0 х_А1 + G₀₂ С_А0 х_А2 =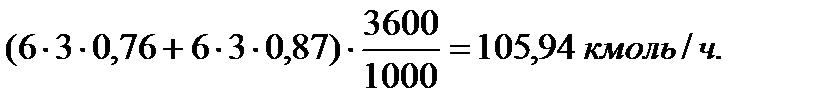

Пример 11.

Реакция проводится в параллельной схеме соединения реакторов РИС-Н и РИВ (рис.5.). Определить распределение объемного потока по реакторам и производительность по продукту R при условии, что степени превращения в реакторах равны.

Дано:

реакция А → 2R;

объемный расход исходного вещества G₀ =100 л/мин;

начальная концентрация исходного вещества С_А0= 2,6 моль/л;

константа скорости реакции k= 0,0205 с ^-1;

Объем реактора вытеснения V_p2= 50 л.

Решение.

Приравниваем уравнения для расчета степеней превращения в реакторе смешения и вытеснения:

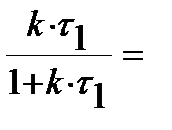
Выражаем 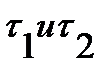через объемы соответствующих реакторов и объемные расходы, поступающие в них, и получаем:

.

Подставляем в полученное выражения значения и получаем:

,

где 1,66- объемный расход смеси, л/с.

Получили нелинейное уравнение, как функцию G₀₁, которое можно решить только графически. Зависимость левой (а) и правой (в) частей уравнения от G₀₁ приведены на рис 6.

Рис.6. Зависимость степени превращения от объемного расхода

В точках пересечения получаем значение G₀₁ и степени превращения вещества x_A в реакторах:

х_А1=0,57; G₀₁=45,3 л/ми_; G₀₂ = G₀ - G₀₁ = 54,7 л/мин.

Рассчитываем производительность установки по продукту R:

П_R=(2G₀₁ С_А0 х_А1 + 2G₀₂ С_А0 х_А2)=

=

Пример 12.

Определить объем реакторов смешения (рис. 7), если входящий поток делится поровну, а степень превращения в реакторе вытеснения равна степени превращения в каскаде реакторов смешения. Объемы реакторов смешения равны.

Дано:

реакция А → R;

объемный расход исходного вещества G₀ =100 л/мин;

константа скорости реакции k= 0,0205 с ^-1;

порядок реакции n=1;

объем реактора вытеснения V_p2= 50 л.

G₀₁

V_p1 V_p2

G₀

V_p3

G₀₂

Рис. 7. Cмешанный тип и схема соединения реакторов

 

Решение.

Определяем степень превращения в реакторе идеального вытеснения:

где

Для каскада реакторов воспользуемся формулой 25 для расчета конечной концентрации в каскаде:

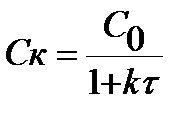или откуда находим время пребывания в одном реакторе смешения каскад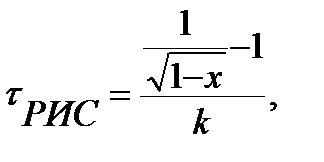а:

а следовательно,

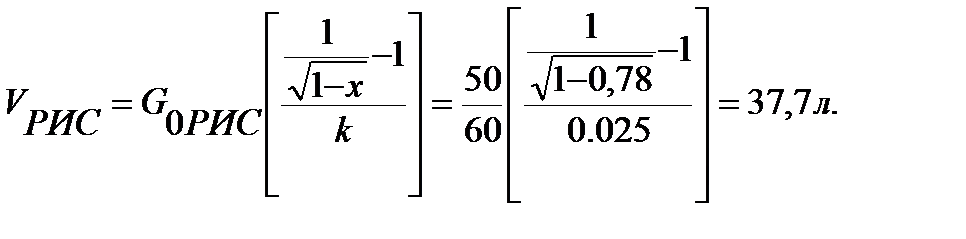
Пример 13.

Рассчитать объемы РИС-Н и РИВ до достижения заданной степени превращения х_А и сравнить их объемы.

Дано:

реакция А+ В = R + S;

концентрация реагента А в потоке, сА, пот - 0,16 моль/л;

Концентрация реагента В в потоке, сВ,­ пот - 0,12 моль/л; Объемный поток реагентов, GV,0 = GV,А + GV,В = 6 м3/ч; Соотношение потоков GV,А / GV,В = 1:3; Константа скорости, К- 5,0 л/моль × мин; Степень превращения, хA - 0,7.

Реагенты А и В загружаются отдельными потоками, смешиваясь в определенном соотношении перед входом в реактор.

Решение.

1. Расчет РИС – Н

Объем реактора рассчитывается по уравнению (6), преобразовав в виде:

,

уравнение скорости реакции

u_r,A = к · с _А,0 (1 – х_A) · с_B,0 (1– х_B).

Определим с_А,0 и с_B,0:

;

.

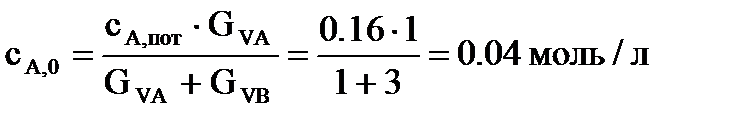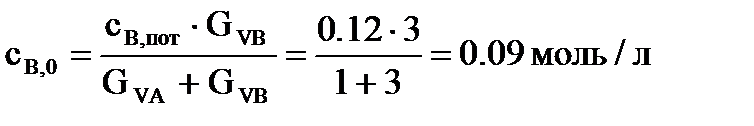Для удобства расчета скорости выразим х_B через х_A:

.

Так как, исходя из стехиометрии, количество А, вступившего в реакцию, равно В, то с_B,0 – с_B = с_А,0 – с_А,

следовательно,

.

Выразим с_B,0 через с_А,0:

, откуда с_B,0 = 2,25 · с _А,0, тогда;

.

Следовательно:

ur,_А = 2,25 · к · с_А,0² (1- х_A) (1- 0,44х_А);

ur,_А = 2,25 · 5 · 0,04² (1-0,7) (1-0,44·0,7) = 37,4·10^-4 моль/л·мин;

.

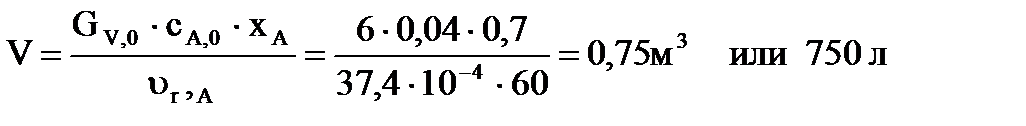2. Расчет РИВ

,

u_r,_А = 2,25 · к · с_А,0² (1 – х_A) (1– 0,44х_А)

Найдем значение интеграла графическим методом. Для этого построим зависимость от (х_A). Принимая значения х_A с шагом 0,1, рассчитаем скорость реакции υ_r (уравнение 6) и обратное значение скорости . Результаты расчета сведем в таблицу 3.

 

Таблица 3. Зависимость скорости реакции от степени превращения

Расчетные величины	Число точек
хA		0,2	0,4	0,5	0,6	0,7
ur*103 моль / л *мин		13,1	8,97	7,02	5,3	3,74
1/ ur л* мин/ моль	56,6	76,3

 

Построим график зависимости обратной скорости от степени превращения и рассчитаем площадь под кривой.

 

Рис. 8. График зависимости обратной скорости реакции от степени превращения

Примечание: для нахождения площади под кривой необходимо:

1) выбрать единицу измерения площади (квадрат, прямоугольник) и определить ее площадь путем умножения значений сторон с учетом размерности. Например, масштаб выбранного прямоугольника (рис.8) будет равен произведению х_А на 1/ υ _r, т.е. 0,1·50=5 л·мин/моль·см²;

2) определить число целых и дробных единиц измерения площади (квадрат, прямоугольник) путем их суммирования;

3) найти площадь умножением полученной суммы на масштаб;

S= 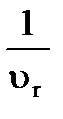= Σs · 50.

Площадь под кривой равна 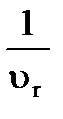= 41,4 л·мин/моль.

Так как G_v,0= 6 м³/час или 0,1 м³/мин,

то V_рив= G_v,0 · c_А,0· 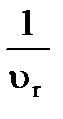= 0,1· 0,04· 41,4 = 0,166 м³ или 166 л.

Сравнивая объемы Vрис-н и Vрив, можно сделать вывод, что РИВ является более эффективным реактором, чем РИС-Н.

Пример 14.

Определить объем одного реактора и время пребывания реагента в каскаде реакторов.

Дано:

реакция А+ В = R + S;

начальная концентрация реагента А с_А,0 = 0,3 моль/л;

степень превращения х_А= 0.7;

объемный расход G_v,o = 20 л/мин;

константа скорости k = 0,38 мин^-1;

число реакторов в каскаде равно 4.

Решение.

1. Объём реактора полного смешения, необходимый для достижения заданного степени превращения, определяем по уравнению:

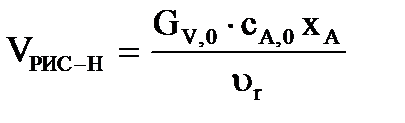, где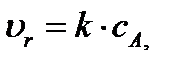

- конечная концентрация реагента А.

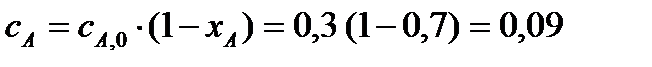моль/л;

.

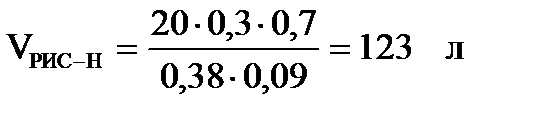2. Среднее время пребывания реагентов в РИС-Н определяем из уравнения (11):

.

Время пребывания в каждом реакторе каскада будет равно:

.

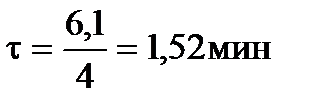Тогда объем реактора в каскаде будет равным:

.

Пример 15.

Определить объем одного реактора в каскаде, полагая, что V₁=V₂=V₃.

 

Дано:

реакция 2А= R + S;

начальная концентрация реагента А_,0 = 1,5 кмоль/м³;

необходимая степень превращения х_А= 0.8 от равновесной;

объемный расход G_v,o = 10 м³/ч;

константа скорости k₁ = 10 м³/(кмоль∙ч);

число реакторов в каскаде равно 3;

константа равновесия Кр =16,0

Решение.

Равновесную концентрацию реагента А определяем из выражения

константы равновесия:

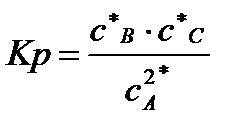
Обозначим равновесные концентрации через y.

Тогда с^*_А = 1,5-2у, с^*_В = с^*_С = y.

Подставляя в уравнение для константы равновесия, получим:

.

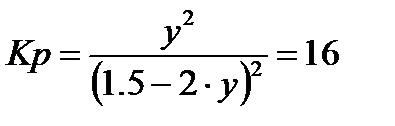Решая уравнение, находим значение у =0,66 кмоль/м³. Полученное значение представляет собой равновесную степень превращения. По условию реагент А прореагирует на 80% от равновесной степени превращения:

х_А= 0,8×0,66 = 0,53 кмоль/м³

Тогда конечная концентрация реагента А составит:

с_А = 1,5- 2×0,533 = 0,43 кмоль/м³

Уравнение скорости реакции в соответствии со стехиометрическим уравнением записываем в виде

или

Зависимость рассчитана при значениях с_А от 1,5 до 0,3 кмоль/м³ с шагом 0,2.

Таблица 4. Расчетные значение скорости реакции и концентрации вещества

сА, кмоль/м3	1,5	1,3	1,1	0,9	0,7	0,5	0,3
,м3/(кмоль×ч)	22,.5	16,9	12,1	8,1	4,9	2,5	0,67

Построим график зависимости от с_А

Рис.9. Графическая зависимость скорости реакции от концентрации вещества

Если из точки на оси абсцисс с_А,0 провести прямую, то получим точку пересечения с кривой в точке а. При проведении процесса в одну ступень получаем (рис 7.3):

,

t = 0,63 ч.

Объем единичного реактора:

V _РИС-Н = G_V,0 × t = 10×0,63 = 6,3 м³.

Примечание: так как по условию объемы трех реакторов одинаковы, то угол наклона проведения прямых к точкам пересечения с кривой будет одинаков. Если уменьшим объем реактора, то для достижения заданной степени превращения необходимо увеличить количество реакторов в каскаде. При этом угол наклона поменяется и будет постоянным для всего количества реакторов в каскаде. Соответственно изменится и время пребывания реагентов в реакторе.