Числовые ряды
1. Осн.понятия:рассмотрим бесконечную пос-ть вещественных чисел U1,U2,U3…Un,где UnЄR.
Опр:числовым рядом наз-ся выр-е вида U1,U2,U3+…+Un+… 
.(1)
Числа U1,U2,U3…Un наз-ся членами ряда. Если n нефиксировать то выр-е для Un наз-ся общим членом ряда. Ряд наз-ся заданным если известем общий член как ф-ия его нмоера, т.е. Un=f(n).
Опр:сумма n первых членов ряда наз-ся n-ной частичной суммой этого ряда. Если n-ю частичную сумму ряда (1) обозначить через Sn, то по определению будем имять: Sn=U1+U2+..+Un(2).
Опр: Суммой ряда наз-ся конечный предел, если он существует, последовательности его n-ных частичных сумм при неограниченном возрастании числа её членов.
!Опр: Ряд наз-ся сходящимся, если он имеет сумму. При этом для сход. ряда(1) пишут 
=S, этим самым выражению придаётся числовой смысл.
Если предел посл-ти частичных сумм Sn не существует или равен ∞,то ряд (1) наз-ся расходящимся.
Опр: Числовой ряд полученный из ряда(1) отбрасыванием n-первых его членов наз-ся остатком или n-ным остатком этого ряда и обозначается: rn=Un+1 + Un+2 +.=. 
.
Очевидно,что дял сход.ряда (1) rn=S-Sn(3)
Теорема! Для того,чтобы числовой ряд (1) сходился необходимо и достаточно, чтобы 
n =0.(2)
Д-во: Необ-ть: пусть ряд(1) сходится, тогда на основании рав-ва rn=S-Sn для сходящегося ряда m= 
Достаточность: пусть выполняется рав-во (2), тогда на основании рав-ва(3) 
=0=> 
=S,т.е.ряд сходится.
Замечание: из ф-лы (3) видно,что сумма сходящегося ряда(1) может с любой степенью точности заменена его n-ной частичной суммой. S=Sn для сход ряда. При этом погрешность не будет первышать| rn|.
Опр.: Суммой(разностью)двух рядов Unи Vn назся-ся ряд 
.
Действия над сходящимися рядами
Т1:Отбрасывание конченого числа первых членов ряда или присоединение в начале его несколько новых членов не влияет на сходимость ряда.
|
|
Д-во:Обозначим через Sn – сумму n первых членов, и через Ck – сумму k отброшенных или добавленных членов. Через Gn+-k сумму (n-+k) членов ряда. Следовательно Sn=Ck+G n-+K (2). Где Ck некоторое число, не зависящее от n. Тогда = 
+ 
. Из этого рав-ва следует,
если предел 
существует и равен конечному пределу, то существует и предел 
и тоже равен конечному числу. И наоборот.
Если бесконечен или не сущ, то это верно и для предела . И наоборот.
T2: Если ряд 
(1) сходится и меет сумму S, то ряд 
(3) сходится и имеет сумму c*S, где C-const.
Д-во: Обозначим частичную сумму ряда (1) через Sn, т.к. ряд (1) сходится, то =S,обозначим Gn-частичная сумма ряда(3) Gn=cU1+CU2+cU3…+cUn.
T3: Сходящиеся ряды можно почленно складывать или вычитать, т.е. если ряд Un и Vn сходятся и их суммы S1 и S2, то и ряды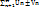 
сходятся и суммы их соответственно рывны S1+-S2.
T4: Члены сходящегося ряда(не переставляя их местами) произвольным образом можно объединить, заключая в скобки: новый ряд будет тоже сходящимся и меть ту же сумму.
Т5: Если ряды 
и 
сходятся и имеют соответственно суммы S1 и S2, а a и b – произвольные числа, то ряд (аU1+bV1)+(aU2+bV2)+..+(aUn+bVn)+.. сходится и сумма его равна aS1+bS2.
Необходимый признак сходимости ряда
Нахождение н-ой частичной суммы и её предела во многих случаях явл. Непростой задачей. Вопрос о сходимости или расходимости рядов можно решить не пользуясь непосредственно определением сходящегося и расходящегося рядов.
Поэтому для выяснения сходимости числовых рядов рассмотрим признаки сходимости. Необходимый признак сходимости выражается след. Теоремой:
|
|
!!!Т:Если ряд U1,U2,U3+…+Un+… сходится, то его общий член стремится к нулю при неограниченном возрастании его номера, т.е. 
=0 (1).
Д-во: Рассмотрим частичные суммы ряда S n-1=U1+U2+..+Un-1;Sn=U1+U2+…+Un;
Un=Sn-S n-1 ,т.к. по условию теоремы ряд сходится, то 
n-1=S и 
=S и тогда = 
n-1)=S-S=0.Для доказательства теоремы нет обратной. Из доказанной теоремы вытекает достаточный признак расходимости: если общий член ряда не стремится к 0 или равен ∞, при n->∞, то ряд расходится.
Условие (1) является необходимым признаком сходимости ряда, но недостаточным.(сущ. Расходящиеся ряды, для кот. выполняется условие(1)).