Циклом в неориентированном графе называется цепь, у которой совпадают начало и конец. Цикл будет называться простым, если в нём нет одинаковых вершин (кроме первой и последней).
Конечная последовательность необязательно различных рёбер E1…..En называется маршрутом длины n, если существует последовательность V1……Vn необязательно различных вершин, что Ei=(Vi-1, Vi).
Маршрут, в котором все рёбра попарно различны называется цепью.
Маршрут, в котором все вершины попарно различны называется простой цепью.
В данном графе не может быть Эйлорова цикла, согласно теореме: Если граф G обладает Эйлоровым циклом, то он является связным, а все его вершины чётными. В нашем случае четыре вершины имеют нечётную степень.
(Эйлоров цикл-путь, проходящий по всем рёбрам графа и притом только по одному разу).

цепь: 1→2→3→4→5→6→7→11→10
простая цепь: a→f→e→d→c→q→a
цикл: a→q→d→e→q→f→a
простой цикл: a→b→c→d→e→f→a
5. Определить центр, диаметр и радиус графа.
Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа. Определим r(i)=max d (i, j), где i, j вершины графа.

| a | b | c | d | e | f | q | |
| a | |||||||
| b | |||||||
| c | |||||||
| d | |||||||
| e | |||||||
| f | |||||||
| q |
(a)=2; r(b)=2; r(c)=2; r(d)=2; r(e)=2; r(f)=2; r(q)=2;
Минимальное из полученных чисел является радиусом графа G, максимальное - диаметром графа G.
В нашем случае:
R=2;
D=2;
Центрами являются все вершины.
Считая граф ориентированным, определить
Степени вершин

Ребро графа называется ориентированным, если одну вершину считают началом ребра, а другую - концом.
Граф, все ребра которого ориентированы, называется ориентированным графом.
Одна и та же вершина ориентированного графа может служить началом для одних ребер и концом для других. Соответственно различают две степени вершины: степень выхода и степень входа.
Степенью выхода вершины А ориентированного графа называется число выходящих из А ребер (обозначение: d+(A)).
Степенью входа вершины А ориентированного графа называется число входящих в А ребер (обозначение: d - (A)).
d+(a)=3; d - (a)=1;+(b)=1; d - (b)=2;+(c)=1; d - (c)=2;+(d)=3; d - (d)=1;+(e)=1; d - (e)=3;+(f)=2; d - (f)=1;+(q)=2; d - (q)=3;
7. Матрицы инцидентности и смежности
Матрица смежности
| a | b | c | d | e | f | q | |
| a | |||||||
| b | |||||||
| c | |||||||
| d | |||||||
| e | |||||||
| f | |||||||
| q |
Матрица инцидентности:
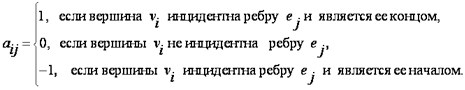
| a | b | c | d | e | f | q | |
| -1 | |||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 |
. Привести примеры пути, ориентированной цепи, простой цепи, контура, цикла и простого цикла

Путём в ориентированном графе от вершины A1 к вершине An называется последовательность ориентированных рёбер A1, A2…..An, в которой конец каждого предыдущего ребра совпадает с началом следующего и каждое ребро в этой последовательности встречается только один раз.
1. a→b→d→q→c - простая цепь
2. b→d→e→q→c-простая цепь
3. a→b→d→e→q→f→e - цепь
Ориентированным циклом называется замкнутый путь в ориентированном графе:
1. a→b→d→q→f→a - простой цикл
2. a→q→c→b→d→q→f→a - цикл
цикл цепь, у которой конечная и начальная вершины совпадают.
Простой цикл не содержит повторяющихся вершин.
Контур - путь, у которого начальная и конечная вершина совпадают.
Простой контур не содержит повторяющихся вершин.
Контур может включать петли в отличии от цикла, в нашем случае контур равен циклу.