Также является
локальной единицей этого кольца, причем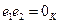 
.
38. Доказать, что, если 
является локальной единицей коммутативного кольца K, то множество
K=K ={ k, k 
K} является подкольцом кольца 
K, прчем
является единицей кольца K.
39. Доказать, что, если
является локальной единицей коммутативного кольца K, 
,
то кольцо K является прямой суммой колец K и 
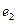K
40. Доказать, что, если 
где k=1,…,n, n 
2, является
локальной единицей коммутативного
кольца K, 
при 
то 
и 
также являются локальными
Единицами кольца K и K является прямой суммой
своих подколец 
K, где i=0,…,n+1.
41. Доказать, что, если 
, где k=1,…,n, n 2, являются ненулевыми попарно
взаимно простыми элементами евклидова кольца К, 
,
то 
где k=1,…,n, n 2, также являются ненулевыми попарно
Взаимно простыми элементами этого кольца. Поэтому существуют
такие 
, где k=1,…,n, что 
Пусть является элементом кольца K/(МК) вычетов кольца К mod M,
т.е. классом вычетов mod M, содержщим 
. Доказать,что является
локальной единицей кольца K и что кольцо 
изоморфно кольцу K/ К.
Доказать, что кольцо K/(МК) изоморфно прямой сумме колец K/ К,. k=1,…,n.
Объяснить, как применяется этот результат к решению систем сравнений.
42. Доказать,что, если 
Является факторизацией числа m, то
Описать изоморфизм декартовой прямой
суммы колец 
на кольцо 
43. Дать определение группы.. Доказать, что множество обратимых элементов кольца 
является абелевой группой.
44. Чьё имя носит функция, ставящая каждому 
, число обратимых элементов кольца ?
45. Дать определение прямого произведения групп..
47 Дать определение декартова прямого произведения групп...
48. Дать определение подгруппы. Дать определение левого (правого) смежного класса группы по подгруппе.
Доказать, что левых смежных классов столько же, сколько правых. Дать определение индекса подгруппы в группе;какобозначается эта величина? Доказать формулу
, где H - подгруппа группы G.
49. Доказать, что, если
Является факторизацией числа m, то группа обратимых элементов кольца является прямым произведением n
Групп, каждая из которых изоморфна группе обратимых элементов соответствующего кольца .
50.Описать группу обратимых элементов кольца 
. Сколько элементов в этой группе?
51.Вывести формулу, связывающую число элементов в группе с числами элементов в подгруппах, прямым произведением ккаой элемент являетсяоторых эта группа является.
52.Вывести выражение для функции Эйлера.
53.Дать определение циклической группы. и циклической подгруппы в данной группе.
55. Дать определение
Порядка элемента в группе. Доказать; что порядок элемента в группе является делителем числа элементов в группе.
- Доказать теоремы Эйлера и Ферма.
57Доказать, что группа обратимых элементов кольца 
есть прямое произведение двух циклических групп второго порядка.
58 Дать определение поля. Доказать, что кольцо 
, где p – простое число
является полем.
59. Дать определение характеристики поля. Чему равна характеристика поля ?
60. Дать определение кольца формальных степенных рядов на полем К. Как обозначается это кольцо? Как определяются операции в этом кольце? Дать определение элемента 
в этом кольце. Как выглядит формальный степенной ряд элемента 
Доказать
ассоциативность свертки. Доказать,что каждый формальный степенной ряд
c 
обратим. Найти обратный элемент к
формальному степенному ряду 
,где 
61. Рассказать о применении формальных степенных рядов к решению разностных
уравнений
62.Дать определение полинома над полем K. Доказать, что полиномы над
полем K образуют подкольцо K[x] кольца K[[x]] формальных степенных
рядов над полем К. Дать определение степени полинома p(x). Как
обозначается степень полинома p(x)? Определить операции над такими полиномами. Могут ли для ненулевого полинома p(x) все p(k), где k пробегает
поле К, быть равными 
? Обосновать алгоритм деления с остатком.
63. Доказать, что кольцо полиномов над полем К является евклидовым колцом.
Как устроена норменная функция 
для этого кольца?
64.Доказать теорему Безу. Доказать, что полином р(х) нд произальным полем К
не может иметь в этом поле больше, чем deg(p) различнпх корней.
65. Дать оределение порядка ord(g) элемента g группы G. Дать оределение
порядка ord 
(g) элемента g группы G относительно ее подгруппы H.
Доказать, что ord (g) | | G|, ord (g) 
[ G:H ], ord (g) | n, если 
.
Доказать, что ord (g) | n, если 
. Доказать, что ord (g) | ord (g).
Доказать, что ord (g) =ord (g),если 
.
66. Доказать, что, если ord (g) =mn, то ord (g 
) =n.
67. Доказать что, если G является абелевй группй, ord (g 
) =n при k=1,2, (n 
,n 
)=1, то ord (g g ) =n n .
68 Доказать что, если G является абелевй группй, ord (g ) =n при k=1,…,r,
и эти n 
попарно взаимно просты, то ord (g …g 
) =n …n .
69 Доказать что, если G является абелевй группй, H является подгруппой группы G
то группа G содержит элемент,
порядок которого относительно H является общим наименьшим
кратным порядков относительно H всех элементов этой группы.
70. Дать определение характеристики поля. Доказать,что если характеристика
поля не равна нулю, то она равна простому числу.
71. Доказать, что,если характеристика поля K равна простому числу p, то
элементы этого поля, представимые в форме n1 
,т.е. 1 сложенной
сама с собой n раз, где n =1,…p, образуют подполе поля K изоморфное
полю F 
= 
/p .
72. Доказать, что,если поле K конечно и состоит из q элементов, то
q= p 
, где p – характеристика поля K, а n – некоторое натуральное
число, причем K является n-мерным линейным пространством
над поле F = /p .
73 Доказать, что группа обратимых элементов любого конечно поля
является циклической.
74. Пуст f=1+p u, где p- простое число, 
, 
,
(v,p)=1. Доказать, что
f 
1+p 
u mod p 
б
f 
1+p uv mod p б
75. Пуст f=1+pu, где p- простое число, 
,(u,p)=1, 
,(v,p)=1.
Доказать,что
f 
1+p uv mod p .
76. Пусть g является первообразным корнем mod p, причем
=1+pu 
,(u,p)=1.
Доказать,что g является первообразным корнем mod p для любого 
77. Пусть g является первообразным корнем mod p, причем
=1+p 
v 
,(w,p)=1.
Доказать,что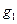 
=g(1+pw)
является первообразным корнем mod p для любого
78.Пусть G – циклическая группа с образующим элементом g,
порядок которого равен n. Пусть d|n, a 
. Вывести необходимое
и достаточное условие разрешимости уравнения уравнения 
=a.
В случае разрешимости солько решений имеет это уравнение.
Как найти все решения этого уравнения, если известно одно из них.
79. Дать определение символа Лежандра. Доказать,что, если (ab,p)=1,то
, 
.
80. Вывести формулу 
.
81. Вывести формулу 
.
82. В случае нечетного а вывести формулу 
.
83. Доказать квадратичный закон взаимности.
84.Дать определение символа Якоби. Вывести формулу
85. Вывести формулу
86. Вывести формулу 
.
87. Пусть g является первообразным корнем mod p 
для любого 
,
где p – нечетное простое число. Объяснить, как найти первообразный
корень mod 2p 
(с доказательством).
88. Объяснить как устроена группа обратимых элементов
кольца 
/2 (без доказательства).
89. Доказать, что любую m 
n-матрицу с элементами из евклидова кольца K
можно с помощью элементарных
преобразований привести к диагональному виду
(1) D = 
,
где 
, 
,если 
90. Доказать,что для любой m n-матрицы A с элементами из евклидова кольца K
существуют такие m m-матрица U с и n n-матрица Vс элементами из
этого кольца,что det(U)= 
, det(V)= , UAV=D, где D является диагональной
матрицей (1) из предыдущего вопроса. Объяснить, как это утверждение
применяется для решения систем линейных уравнений в целых числах.
91. Дать определение квадратичного поля К. Дать определение
инволюции (сопряжения) в таком поле. Дать определение следа и нормы элемента
этого поля. Дать определение кольца 
целых элементов поля К. Доказать,что
любой элемент z из однозначно представим в форме a+b 
,где
,если 
,если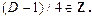 
.
92. Какие кольцах целых чисел в квадратичных полях
вам известны как евклидовы (без доказательства). Доказать, что
кольцо целых гауссовых чисел является евклидовым.
44. Доказать, что, если p – нечётное простое число, то группа обратимых элементов кольца вычетов является циклической
45. Дать определение индекса обратимого элемента кольца
46..Описать структуру группы обратимых элементов кольца 
47. Дать определение квадратичного вычета Доказать, что если p – нечётное простое число, то существует ровно (p-1)/2
Квадратичных вычетов и (p-1)/2 квадратичных невычетов в группе обратимых элементов поля
48. Дать определение символа Лежандра и вывести его свойства.
49. Вывести квадратичный закон взаимности
50. Дать определение символа Якоби и вывести его свойства
51. Рассказать о применении символа Якоби.
52. Рассказать о решении сравнения 
4. Сформулировать принцип математической индукции.
5. Доказать формулу бинома Ньютона.