Введение
Гидравлика – это наука, изучающая законы равновесия и механического движения жидкостей и разрабатывающая методы применения этих законов для решения прикладных задач. Главнейшие области применения гидравлики – гидротехника, мелиорация и водное хозяйство, гидроэнергетика, водоснабжение и канализация, водный транспорт, машиностроение, авиация и т.д.
Данная курсовая работа выполняется с целью закрепления знаний, полученных при самостоятельном изучении дисциплины «Гидравлика», и приобретения практического применения этих знаний для решения инженерных задач.
Курсовая работа делится на две части: теоретическую и практическую. В теоретической части рассмотрены две темы: формирование параболического профиля скоростей на начальном участке ламинарного течения и неустановившееся течение жидкости. В практической части предусмотрено решение задач по следующим темам: определение давления в покоящейся жидкости; определение силы давления жидкости на плоские стенки; определение силы давления жидкость на криволинейные поверхности; относительный покой жидкости; решение задач с применением закона Архимеда; определение расхода при истечении жидкости через отверстия и насадки; применение уравнения Бернулли для решения задач механики.
Справочные данные, необходимые для решения задач, приведены в справочной литературе.
Курсовая работа выполнена после тщательного изучения, указанных выше тем, по перечисленной использованной литературе.
Теоретическая часть
Равномерное вращение сосуда с жидкостью.
 Возьмем открытый цилиндрический сосуд с жидкостью и
Возьмем открытый цилиндрический сосуд с жидкостью и
сообщим ему постоянную угловую скорость  вращения вокруг
вращения вокруг
его вертикальной оси. Жидкость по-
степенно приобретет ту же угловую
скорость, что и сосуд, а свободная поверхность ее видоизменится: в централь-
ной части уровень жидкости понизится, у стенок — повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис.
1).
На жидкость в этом случае будут
действовать две массовые силы, сила
тяжести и центробежная сила, которые,
будучи отнесенными к единице массы,
соответственно равны 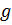 и
и  .
.
Равнодействующая массовая сила 
увеличивается с увеличением радиуса
за счет второй составляющей, а угол
наклона ее к горизонту уменьшается.
Эта сила нормальна к свободной поверхности жидкости, в связи, с
чем наклон этой поверхности с увеличением радиуса возрастает.
Найдем уравнение кривой  в системе координат
в системе координат  и
и 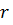 с началом в центре дна сосуда. Учитывая, что сила у является нормалью к кривой
с началом в центре дна сосуда. Учитывая, что сила у является нормалью к кривой  , из чертежа найдем, что
, из чертежа найдем, что

Отсюда

или после интегрирования
 (1)
(1)
В точке пересечения кривой  с осью вращения
с осью вращения  ,
,
поэтому окончательно будем иметь, т. е. кривая  является параболой, а свободная поверхность
является параболой, а свободная поверхность
жидкости — поверхностью параболоида вращения.
Пользуясь уравнением (1), можно определить положение
свободной поверхности в сосуде, например максимальную высоту
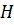 подъема жидкости и высоту
подъема жидкости и высоту  расположения вершины параболоида при данной скорости вращения
расположения вершины параболоида при данной скорости вращения  . Однако для этого
. Однако для этого
необходимо использовать еще уравнение объемов: объем неподвижной жидкости равен
ее объему во время вращения.
 На практике чаще все-
На практике чаще все-
го приходится иметь дело
с таким случаем вращения
сосуда с жидкостью, когда
ось вращения расположена горизонтально (или
произвольно), а угловая
скорость  столь велика,
столь велика,
что силой тяжести можно
пренебречь по сравнению
с центробежными силами.
Закон изменения давления в жидкости для это-
го случая легко получить
из рассмотрения уравнения равновесия элементарного объема с
площадью основания  и высотой
и высотой  , взятой вдоль радиуса
, взятой вдоль радиуса
(рис. 2). На выделенный элемент жидкости действуют силы
давления и центробежная сила. Обозначив давление в центре
площадки  , расположенной на радиусе
, расположенной на радиусе  , через
, через  , а в центре другого основания объема (на радиусе
, а в центре другого основания объема (на радиусе 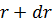 ) через
) через  , получим следующие уравнение равновесия выделенного объема в направлении радиуса:
, получим следующие уравнение равновесия выделенного объема в направлении радиуса:
 ,
,
или
 .
.
После интегрирования

Постоянную  найдем из условия, что при
найдем из условия, что при 
 .
.
Следовательно,

Подставив ее значение в предыдущее уравнение, получим связь
между  и
и  в следующем виде:
в следующем виде:
 (2)
(2)
Очевидно, что поверхностями уровня в данном случае будут
цилиндрические поверхности с общей осью — осью вращения
жидкости. Если сосуд лишь частично заполнен жидкостью, то
ее свободная поверхность, как одна из поверхностей уровня, также
будет цилиндрической, причем именно ее радиус, удобно обозначить через 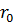 , а давление на ней через
, а давление на ней через  .
.
Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси
вращения (или на кольцевую часть этой стенки).
Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку радиусом 
и шириной  . Используя формулу (2), получим
. Используя формулу (2), получим

а затем следует выполнить интегрирование в требуемых пределах.
При большой скорости вращения жидкости можно получить
весьма значительную суммарную силу давления на стенку. Это
используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил
нормального давления. Способом, указанным выше, пользуются
для подсчета силы осевого давления жидкости на рабочие колеса
центробежных насосов.
Те же формулы для рассмотренного случая относительного
покоя можно вывести путем интегрирования дифференциального
уравнения равновесия жидкости. Поместив начало
координат в центре дна сосуда и направив ось вертикально вверх,
получим
 ;
;
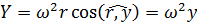 ;
;  .
.
Подставляя эти величины в уравнение, получим
 ,
,
или
 .
.
Если учесть, что
 ,
,
то после интегрирования
 .
.
При  и
и 
 , следовательно,
, следовательно,
 .
.
В результате окончательно получим
 .
. 
Уравнение свободной поверхности жидкости может быть по-
лучено, если в этом уравнении положить  . После сокращений и преобразования
. После сокращений и преобразования

что вполне совпадает с ранее полученной
формулой (1).
Если в предыдущем выводе пренебречь си-
лой тяжести  , а постоянную интегри-
, а постоянную интегри-
рования определить из условия, что при
 ,
,  , то получим уже известную
, то получим уже известную
формулу (2).
Внезапное расширение русла.
Значение коэффициентов местных сопротивлений в большинстве случаев получается и опытов, на основании которых выводятся экспериментальными формулы или строятся графики.
 Однако для случаев внезапного расширения достаточно найти чисто теоретическим путем.
Однако для случаев внезапного расширения достаточно найти чисто теоретическим путем.
Внезапное расширение русла и соответствующая ему схема течения жидкости показана на рис 3. Поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии в данном случае. При этом, как показываются наблюдения, происходит непрерывный обмен частицами жидкости между основным потоком и завихренной его частью.
Рассмотрим два сечения горизонтального потока:  – в плоскости расширения трубы и
– в плоскости расширения трубы и  – в том месте, где поток, расширения, заполнит все сечения широкой трубы. Поэтому второй пьезометр показывает высоту, на
– в том месте, где поток, расширения, заполнит все сечения широкой трубы. Поэтому второй пьезометр показывает высоту, на  больше, чем первый; но, если потерь напора в данном месте не было, то второй пьезометр показал бы еще большую высоту. Та высота
больше, чем первый; но, если потерь напора в данном месте не было, то второй пьезометр показал бы еще большую высоту. Та высота 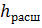 , которую мы здесь как бы недополучаем, и есть местная потеря напора на расширение
, которую мы здесь как бы недополучаем, и есть местная потеря напора на расширение
Обозначим давление, скорость и площадь сечения потоков сечении  соответственно через
соответственно через  , а в сечении
, а в сечении 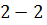 через
через 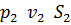 .
.
Прежде чем составлять исходное уравнение, сделаем следующих три допущения:
1) распределение скоростей в сечения  и
и  равномерное, т.е.
равномерное, т.е. 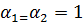 ;
;
2) касательное напряжение на стенке трубы между сечениями  и
и  равно нулю (
равно нулю ( );
);
3) давление  в сечении
в сечении  действует по всей площади
действует по всей площади  .
.
Запишем для сечения 1-1 и 2-2 уравнение Бернулли с учетом потери напора 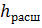 на расширение и, принимая
на расширение и, принимая  , получим
, получим
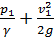 =
= 
Затем применим теорему механики об изменении количества давления к цилиндрическому объему, заключенному между сечением 1-1 и 2-2 и стенкой трубы. Для этого определим импульс внешних сил, действующих на рассматриваемый объем в направлении движения, т.е. сил давления. Учитывая, что площади цилиндра слева и справа одинаковы и равны  , а так же считая, что в сечении 1-1 давление
, а так же считая, что в сечении 1-1 давление  равномерно распределено по всей площади
равномерно распределено по всей площади  , получим секундный импульс сил в виде
, получим секундный импульс сил в виде
 .
.
Соответствующее этому импульсу изменение количества движения определится как разность между секундным количеством давления, выносимым из рассматриваемого объема и вносимым в него; при равномерном распределении скоростей по сечениям эта разность равно
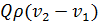 .
.
Приравнивая одно к другому и заменяя  через
через  , получим
, получим

Разделим уравнение на  , учитывая, что
, учитывая, что  , и преобразуем правую часть уравнения
, и преобразуем правую часть уравнения
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  .
.
Сгруппировав члены, получим

Сравнение полученного уравнения с ранее записанным уравнение Бернулли показывает полную их аналогию, откуда делаем вывод, что

Потеря напора (удельной энергии) при внезапном расширении русла равна скоростному напору, подсчитанному по разности скоростей. Это положение часто называют теоремой Борда – Карно в честь французских ученых.
Если учесть, что согласно уравнению расхода

То полученный результат можно записать ещё в следующем виде, соответствующем общему способу выражения местных потерь:
 .
.
Следовательно, для случая внезапного расширения русла коэффициент сопротивления
 .
.
Доказанная теорема, как и следовала ожидать, хорошо подтверждается опытом при турбулентном течении и широко используется в расчетах.
В том частном случае, когда площадь  весьма велика по сравнению с площадью
весьма велика по сравнению с площадью  и, следовательно, скорость
и, следовательно, скорость  можно считать равной нулю, потеря на расширение
можно считать равной нулю, потеря на расширение
 ,
,
т.е. в этом случае теряется весь скоростной напор (вся кинетическая энергия, которая обладает жидкость); коэффициент сопротивления в это случае  .такому случаю соответствует, например, подвод жидкости по трубке к резервуару достаточно больших размеров.
.такому случаю соответствует, например, подвод жидкости по трубке к резервуару достаточно больших размеров.
Рассмотренная потеря напора (энергии) при внезапном расширении русла расходуется, можно считать, исключительно на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание непрерывного вращательного движения жидких масс и постепенное их обновление (обмен). Поэтому этот вид потерь энергии, пропорциональных квадрату скорости (расхода), называет потерями на вихреобразование. Эти потери расходуются на работу сил трения, но не непосредственно, как в прямых трубок постоянного сечения, а через вихреобразование.
Практическая часть
Задача 1.1
В закрытом резервуаре налита вода. Определить высоту h поднятия ртути в дифманометре и высоту  поднятия воды в закрытом пьезометре, если показание пружинного манометра, подключенного на уровне точки А, равно
поднятия воды в закрытом пьезометре, если показание пружинного манометра, подключенного на уровне точки А, равно  (рисунок 1.1). Атмосферное давление
(рисунок 1.1). Атмосферное давление  считать нормальным, глубина погружения точки А равна
считать нормальным, глубина погружения точки А равна  . Плотность ртути
. Плотность ртути  , воды
, воды  .
.

Рисунок 1.1
Таблица исходных данных:
| Высота, м | Манометрическое давление в точке А на глубине 
|
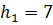
| 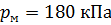
|
Решение:
Находим давление в точке А:

Отсюда находим давление  :
:

Найдем высоту  поднятия ртути в дифманометре из уравнения:
поднятия ртути в дифманометре из уравнения:

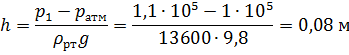
Определяем высоту  поднятия воды в закрытом пьезометре из уравнения:
поднятия воды в закрытом пьезометре из уравнения:
 или
или

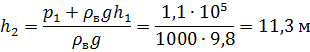
Ответ: 
Задача 1.3
В цилиндрическом сосуде диаметром  и высотой
и высотой  налита вода с начальным уровнем
налита вода с начальным уровнем  (рисунок 1.3). Определить:
(рисунок 1.3). Определить:
1) Будет ли выплескиваться вода, если сосуд будет вращаться с постоянной частотой вращения  ?
?
2) На каком расстоянии  от дна будет находиться самая низшая точка свободной поверхности?
от дна будет находиться самая низшая точка свободной поверхности?
3) С какой частотой нужно вращать сосуд, чтобы вода поднялась до краев сосуда?

Рисунок 1.3
Таблица исходных данных:
| Высота, м | Диаметр, м | Частота вращения, мин-1 |
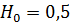

| 
| 
|
Решение:
Определяем угловую скорость:

Определяем наибольшую разницу уровней между низшей точкой свободной поверхности в центре и наивысшей у боковой стенке:

Наибольшее понижение свободной поверхности на оси вращения по сравнению с первоначальным уровнем воды в сосуде равно:

Из равенства объемов следует: объем жидкости  - объем параболоида
- объем параболоида  , след.:
, след.:
 ,
, 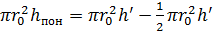 (3)
(3)

 из формулы (3)
из формулы (3)
Наибольшее повышение уровня у боковых стенок над первоначальным уровнем воды в сосуде:

 из формулы (3)
из формулы (3)
Наиболее пониженная точка свободной поверхности В находится от дна на расстоянии:

По отношению ко дну точка С как самая высокая точка свободной поверхности находится на расстоянии:

Для того, чтобы вода поднялась до краев сосуда, необходимо вращать сосуд с частотой:

Имеем  - центробежное ускорение у стенки. Для того, чтобы вода не выплескивалась при вращении сосуда с постоянной данной в условии частотой вращения, необходимо, чтобы выполнялось условие:
- центробежное ускорение у стенки. Для того, чтобы вода не выплескивалась при вращении сосуда с постоянной данной в условии частотой вращения, необходимо, чтобы выполнялось условие:
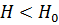

Т.к.
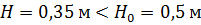
Вода выплескиваться не будет.
Ответ: 1) не будет; 2)  ; 3)
; 3) 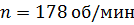
Задача 1.5
 Треугольное отверстие АВС в вертикальной стенке закрытого резервуара, представляющее равносторонний треугольник, закрыто щитом (рисунок 1.5). Определить равнодействующую силу гидростатического давления бензина на щит и точку ее приложения, если заданы линейные размеры:
Треугольное отверстие АВС в вертикальной стенке закрытого резервуара, представляющее равносторонний треугольник, закрыто щитом (рисунок 1.5). Определить равнодействующую силу гидростатического давления бензина на щит и точку ее приложения, если заданы линейные размеры:  и манометрическое давление
и манометрическое давление  на свободной поверхности бензина.
на свободной поверхности бензина.
Рисунок 1.5
Таблица исходных данных:
| Линейные величины, м | Манометрическое давление, мм.рт.ст |

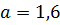
| 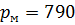
|
Решение:
Гидростатическое давление изменяется по закону:
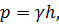
где  .
.
Избыточное гидростатическое давление на АВ с учетом  будет равно:
будет равно:
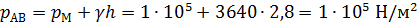
Давление в точке С равно:

Среднее значение гидростатического давления равно:

Площадь треугольника АВС:

Равнодействующее гидростатическое давление равно:

где  - центр тяжести треугольника под нижней свободной поверхностью жидкости. Как известно центр тяжести равностороннего треугольника лежит на расстоянии 1/3 высоты треугольника, т.е.
- центр тяжести треугольника под нижней свободной поверхностью жидкости. Как известно центр тяжести равностороннего треугольника лежит на расстоянии 1/3 высоты треугольника, т.е.

Определяем равнодействующую силу гидростатическое давление бензина на щит и точку ее приложения:

В нашем случае центр давления совпадает с центром тяжести равностороннего треугольника.
Ответ: 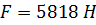
Задача 1.7
Под каким давлением  (рисунок 1.7) нужно подать жидкость в безштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо, преодолевая силу
(рисунок 1.7) нужно подать жидкость в безштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо, преодолевая силу  на штоке, если давление в штоковой полости
на штоке, если давление в штоковой полости  ? На какую силу сжатия
? На какую силу сжатия  нужно отрегулировать пружину предохранительного клапана, чтобы он открывался при возрастании силы на штоке до величины
нужно отрегулировать пружину предохранительного клапана, чтобы он открывался при возрастании силы на штоке до величины  , если диаметр входного отверстия (седла) клапана
, если диаметр входного отверстия (седла) клапана  , а давление
, а давление  . Силы трения не учитывать.
. Силы трения не учитывать.

Рисунок 1.7
Таблица исходных данных:
| Диаметр, мм | Давление, МПа | Сила, Н |
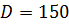


| 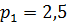
| 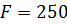
|
Решение:
1) Для движения штока необходимо, чтобы сила давления в бесштоковой полости равна  +сила давления от
+сила давления от  . Таким образом:
. Таким образом:

где 
Следовательно,

Отсюда выражаем давление, под которым нужно падать жидкость в бесштоковую полость гидроцилиндра, чтобы поршень начал двигаться вправо:


2) При силе на штоке в 
 в бесштоковой полости:
в бесштоковой полости:

Для открытия клапана необходимо равенство сил слева и справа от него:

Определяем силу сжатия  , на которую нужно отрегулировать пружину предохранительного клапана, чтобы он отрывался при возрастании силы на штоке до величины
, на которую нужно отрегулировать пружину предохранительного клапана, чтобы он отрывался при возрастании силы на штоке до величины  :
:


Ответ: 
Задача 1.9
Определить осадку 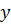 и проверить остойчивость плавания в воде деревянного бруса (рисунок 1.9). Размеры бруса: высота
и проверить остойчивость плавания в воде деревянного бруса (рисунок 1.9). Размеры бруса: высота  , ширина
, ширина  , длина
, длина  . Относительная плотность бруса
. Относительная плотность бруса  . Вычислить наименьшую высоту
. Вычислить наименьшую высоту  , при которой брус будет еще остойчив.
, при которой брус будет еще остойчив.

| Рисунок 1.9 |
Таблица исходных данных:
| Относительная плотность | Плотность воды, кг/м3 | Длина, м | Ширина, м | Высота, м |

| 
| 
| 
| 
|
Решение:
Для определения осадки бруса записываем условие плавания:

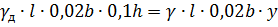

Относительная плотность бруса:
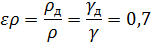

Поскольку брус – однородное прямоугольное тело, его центр тяжести (т.С) находится на середине высоты  . Центр водоизмещения (т. D) лежит в центре тяжести объема погруженной части
. Центр водоизмещения (т. D) лежит в центре тяжести объема погруженной части  , т.е. на высоте
, т.е. на высоте  от нижней кромки бруса. Т.к. т.С выше т.D на величину:
от нижней кромки бруса. Т.к. т.С выше т.D на величину:

Для проверки остойчивости тела необходимо вычислить величину метацентричного радиуса  .
.
Находим центральный момент инерции плоскости ватерлинии относительно продольной оси:

Тогда по формуле:
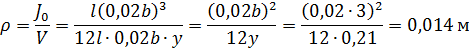
Т.к.  , то брус не устойчив.
, то брус не устойчив.
Ответ: 
Задача 1.11
В вертикальной стенке, разделяющей резервуар на две части, расположено круглое отверстие с диаметром  и насадкам длиной
и насадкам длиной  (рисунок 1.11). В наружной стенке имеется другое отверстие диаметром
(рисунок 1.11). В наружной стенке имеется другое отверстие диаметром  . Центры обоих отверстий расположены на высоте
. Центры обоих отверстий расположены на высоте  от дна. Уровень воды в левой части резервуара
от дна. Уровень воды в левой части резервуара  , расход через отверстия
, расход через отверстия  . Определить уровень
. Определить уровень  воды в правой части резервуара и диаметр
воды в правой части резервуара и диаметр  отверстия в наружной стенке.
отверстия в наружной стенке.

Рисунок 1.11
Таблица исходных данных:
| Параметр | Расход, л/с | Вид насадка |



| 
| конический сходящийся |
Решение:
Осредненные значения коэффициентов для режима истечения жидкости через конический сходящийся насадок для маловязких жидкостей (в нашем случае вода) следующие:

Коэффициент сжатия  находим из соотношения:
находим из соотношения:


Запишем уравнение расхода  :
:

Из этого уравнения находим скорость истечения в сжатом сечении струи:
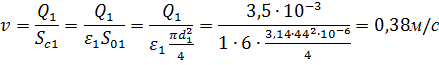
Определяем расчетный напор:


Так как  , то и
, то и 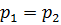 . Тогда:
. Тогда:

Отсюда находим уровень воды в правой части резервуара:
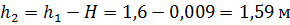
Запишем уравнение расхода 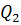 :
:
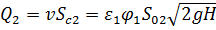



Ответ: 
Задача 1.13
Центробежный насос подает воду температурой  в систему (рисунок 1.13). Расход воды составляет
в систему (рисунок 1.13). Расход воды составляет  . Всасывающая труба насоса диаметром
. Всасывающая труба насоса диаметром 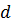 , общей длиной
, общей длиной  имеет два поворота под углом 90° и приемный клапан, коэффициент сопротивления которого
имеет два поворота под углом 90° и приемный клапан, коэффициент сопротивления которого  . Определить максимально возможную высоту установки оси насоса
. Определить максимально возможную высоту установки оси насоса  над уровнем воды в отстойнике, исходя из условия, что давление воды при входе в насос должно быть на 0,02МПа выше давления парообразования, равного
над уровнем воды в отстойнике, исходя из условия, что давление воды при входе в насос должно быть на 0,02МПа выше давления парообразования, равного  . Абсолютное давление на свободной поверхности жидкости в отстойнике принять равным 0,1 МПа. Эквивалентная шероховатость поверхности трубы
. Абсолютное давление на свободной поверхности жидкости в отстойнике принять равным 0,1 МПа. Эквивалентная шероховатость поверхности трубы  , плотность воды
, плотность воды  .
.

Рисунок 1.13
Исходные данные: 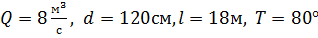 С.
С.
Решение:
Запишем уравнение Бернулли для всех сечений:
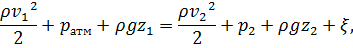
где  - средняя скорость течения воды на свободной поверхности водоема;
- средняя скорость течения воды на свободной поверхности водоема;  - атмосферное давление;
- атмосферное давление;  - средняя скорость течения воды во всасывающей трубе;
- средняя скорость течения воды во всасывающей трубе;  - потери давления.
- потери давления.

Высота расположения оси насоса над уровнем воды отстойника:


При 80°С: 
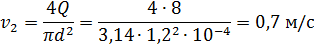
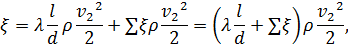
где  .
. 
Число Рейнольдса:

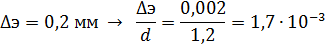
Коэффициент гидравлического сопротивления:

Коэффициент сопротивления на поворот:
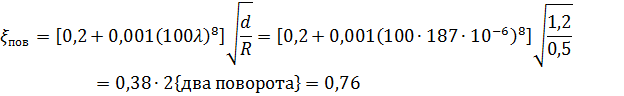


Максимальная высота расположения оси насоса над уровнем воды отстойника:

Ответ: 
Заключение
В данной курсовой работе мною была достигнута основная поставленная цель: закрепления знаний, полученных при самостоятельном изучении дисциплины «Гидравлика», и приобретение практического применения этих знаний для решения инженерных задач.
В курсовой работе я рассмотрела теоретическую часть по дисциплине «Гидравлика». В моей теоретической части затронуты два вопроса, входящие в программу изучения дисциплины: формирование параболического профиля скоростей на начальном участке ламинарного течения и неустановившееся течение жидкости. Эти два вопроса рассмотрены мною в полном объеме.
Во второй части моей курсовой (практической части) были решены задачи последующим темам: определение давления в покоящейся жидкости; определение силы давления жидкости на плоские стенки; определение силы давления жидкость на криволинейные поверхности; относительный покой жидкости; решение задач с применением закона Архимеда; определение расхода при истечении жидкости через отверстия и насадки; применение уравнения Бернулли для решения задач механики. С помощью данной практической мною были усвоены и закреплены многие теоретические знания дисциплины. Я также стала лучше разбираться в теории и нашла связь этой теории с практикой.
Данная кур