Согласно рис. 1 параметры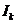 
и 
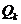можно представить в виде
; 
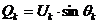(4),
где 
и 
.
Величины 
и 
- координаты той же точки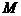 
на сигнальном
созвездии в полярной системе координат. Подставив (4) в (3) преобразуем сигнал (3) к виду
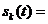
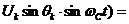
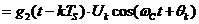(5).
Из (5) видно, что в состав выделенного сигнала в качестве сомножителя входит гармоническое колебание,
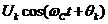(6)
в канонической форме*).
Представление гармонического колебания (6) в канонической форме в составе сигнала (5) получено благодаря знаку минус в выражении (1) перед вторым слагаемым. Этот знак обеспечивается введением инвертора в нижнюю ветвь перед сумматором на структурной схеме.
Гармоническому колебанию (6) соответствует комплексная амплитуда,
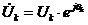(7).
Комплексная амплитуда (7) при условии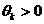 
представлена вектором 
на комплексной плоскости (рис. 2а).
------------------------------------------------------------------------------------------------
*) Как следует из учебников и учебных пособий теории электрических цепей и теории сигналов [5,6,7,8,9] при записи гармонического колебания в канонической форме перед начальной фазой должен стоять знак плюс, как в выражении (6). При этом численное значение начальной фазы в каждом конкретном случае может быть величиной положительной или отрицательной. Представление гармонического колебания по форме 
не является каноническим, так как ее использование приводит к ненужным осложнениям.
Рис. 2а Вектор комплексной амплитуды ,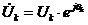
2б Вектор комплексной амплитуды 
.
Существенно, что вектор по длине и направлению полностью соответствует исходному вектору, проведенному в точку 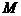с координатам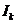и и 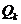на сигнальном созвездии на рис. 1.
В выражении (5) гармонический сигнал представлен в канонической форме. Поскольку сигнал (5) был получен из сигнала (1), то выражение (1) является канонической формой для сигналов квадратурных видов модуляции (КАМ, КМФ).
Если в структурной схеме исключить инвертор перед сумматором,
тогда сигнал на выходе сумматора будет представлен в виде
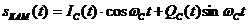(8).
В этом случае, повторив приведенные выше выкладки, в составе выделенного сигнала получим гармонический сигнал в форме , которая не является канонической, как упоминалось ранее.
Вектор комплексной амплитуды для данного гармонического сигнала будет иметь вид , и на комплексной плоскости этот вектор при условии 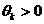изображен на рис. 2б.
Сравнивая рис. 2б и рис. 1 делаем вывод, что при задании сигнала
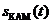в форме (8) вектор на комплексной плоскости не совпадает по направлению с соответствующим вектором на сигнальном созвездии на рис. 1. Это является следствием того, что форма (8) не является канонической для представления сигнала КАМ и от этого возникает отмеченное несоответствие.
Таким образом, из двух возможных представлений сигнала квадратурной модуляции в форме (1) или в форме(8), будем считать только форму (1) канонической и только ее будем использовать в КР.
Отметим, что правая часть выражения (5) является квазигармонической формой для сигнала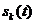 
. Она таковой является потому, что функция 
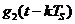не принимает отрицательных значений. Функция 
определяет форму огибающей сигнала .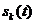
При определении корреляционной функции случайного сигнала на выходе модулятора необходимо уточнить задание ансамблей случайных процессов на выходах перемножителей.
При задании ансамблей этих процессов предполагается, что имеется ансамбль одинаковых устройств, по которым передаются разные реализации случайных процессов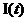 
и 
. В состав каждого передающего устройства (ПерУ) входит свой генератор гармонического колебания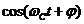 
, где начальная фаза 
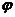принимает какое-то детерминированное численное значение. Множество этих различных значений 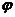образует случайную величину 
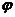, то есть каждое является реализацией случайной величины .
При задании случайных процессов на выходе перемножителей, детерминированные функци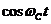и 
и 
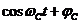, входящих в (1), необходимо расширить до случайных функций 
и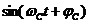 
введением в аргумент детерминированных функци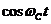й и случайной фазы , и тогда вместо (1) получим случайный процесс следующего вида
(9).
На рис. 4 рассмотрен пример по выполнению задания к разделу модулятор.
Рис. 4 Пример построения графиков для сигналов КАМ в блоке модулятора.
Выражение (9) позволяет правильно определить корреляционную функцию случайного сигнала КАМ или КФМ на выходе сумматора.
Обращаем внимание на случайную фазу . В каждой отдельной реализации случайного процесса, определенного по формуле (9), фаза имеет свое численное значение, которое не изменяется во времени. Случайный же характер фазы проявляется в том, что для разных реализаций значения отличаются друг от друга и ансамбль этих значений образует случайную величину с равномерной плотностью вероятности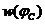 
на интервале 
(рис. 5).
Рис. 5 Равномерная плотность вероятности .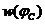
Только при равномерной плотности вероятности 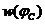для случайной фазы (рис. 5) случайный процесс на выходе модулятора (на выходе сумматора) будет стационарным. В случае отличия плотности вероятности 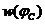от равномерной условие стационарности выполняться не будет. Корреляционная функция сигнала 
в этом случае будет зависеть отдельно от моментов времен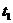и 
и 
, а не от их разности 
, как это требуется для стационарных процессов.
КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ и СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ МОЩНОСТИ
случайных процессов на выходе перемножителей.
На выходе верхнего перемножителя (ПМ-1) получаем сигнал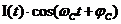 
. Определим математическое ожидание этого случайного сигнала
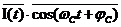(10).
Это равенство получено на основании того, что сомножители 
и
представляют собой независимые случайные процессы (ранее отмечалось о независимости случайной фазы от сигнала ).
Случайный процесс равный
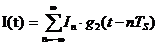(11),
формируется на выходе блока ФМС при подаче на его вход случайного процесса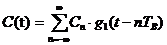 
с выхода блока кодера (К). Определим 
и 
, входящие в (10)
= 
= 
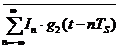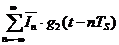(12),
где 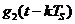- детерминированный сигнал.
Согласно (8) из «П4 к блоку ФМС» можем написать
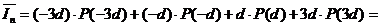
0 (13).
Подставляя (13) в (12), получим
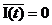(14).
Следовательно, - центрированный процесс.
Математическое ожидание сигнала , зависящего от случайной величины с равномерной плотностью вероятности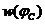
на интервале , определим по формуле
= 
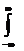
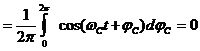(15).
Подставляя (14) и (15) в (10), получим 
. Это равенство означает, что случайный процесс 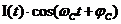является центрированным, поэтому корреляционная функция 
этого процесса определяется в виде
= 
= 
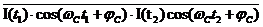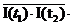
, (16)
где
= 
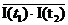(17).
- детерминированная функция.
Аналогично (15), получим 
и выражение (16) примет окончательный вид
(18).
Из равенства (18) следует, что случайный сигнал 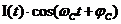на выходе перемножителя обладает свойством стационарности, так как математическое ожидание этого сигнала постоянно, корреляционная функция зависит от разности времен 
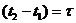. Тогда (18) будет иметь вид
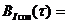
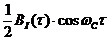(19).
На рис. 6 представлен график функции 
, определенный по (19)
Рис. 6 График корреляционной функции случайного процесса .
Нетрудно показать, что имеет место равенство.
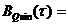
(20).
Спектральную плотность мощности сигнала на выходе перемножителя определим на основании теоремы Винера-Хинчина (рис. 7). Преобразуя функцию по Фурье, получим
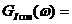
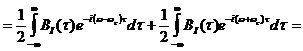
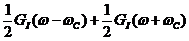(21)
Рис. 7 График функции 
.
Также из (21) следует 
.
Корреляционная функция и спектральная плотность мощности случайного процесса на выходе модулятора.
Сигнал на выходе модулятора является сигналом на выходе сумматора и, ссылаясь на (10) равен
= 
- 
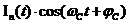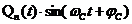(22).
Обратив внимание на выражения (14) и (15), можно утверждать, что случайный сигнал является центрированным случайным процессом, поэтому его корреляционная функция будет равна
= 
-
- 
=
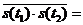
после преобразований получим
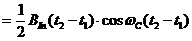
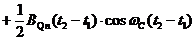(23).
Этот результат получен на основании того, что 
и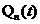 
являются независимыми случайными процессами, поэтому
; 
, обозначив 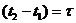и учитывая, что
из (26) получим
(24).
Сравнивая (27) с (20) делаем вывод, что с точностью до множителя 
функция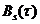 
равна функции 
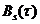. Также с точностью до множителя форма графика соответствует форме графика (рис. 6).
Преобразуя (27) по Фурье найдем спектральную плотность мощности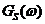 
сигнала на выходе модулятора. Спектральная плотность 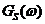с точностью до множителя будет равна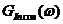 
, определяемая (25) и рис. 6.
П6 к блоку ДЕМОДУЛЯТОР
и преобразователь параллельного кода в последовательный код.
Информационный сигнал (ИС) с выхода модулятора поступает в непрерывный канал (НК), существенно ослабляется (на несколько порядков) за счет различных потерь мощности в НК.
В данной КР аппаратура в составе НК между выходом модулятора и входом в линию связи (ЛС), а также между выходом ЛС и демодулятором (ДМ) не рассматривается)*.
Поэтому, прежде чем принятый ИС поступит на вход демодулятора, его усиливают в соответствующее число раз. В КР будем считать, что мощность ИС на входе демодулятора равна мощности этого сигнала на выходе модулятора.
------------------------------------------------------------------------------------------------
*) Общие представления о данной аппаратуре даются в курсе лекций и [2 глава 8]. В передающем устройстве в состав аппаратуры входят усилительное устройство (УУ) и устройство уплотнения сигналов. В приемном устройстве, соответственно, входят устройство разделения сигналов и УУ.
Но на вход усилительного устройства (УУ), расположенного перед демодулятором, помимо сильно ослабленного ИС поступает также сигнал аддитивной флуктуационной помехи (АФП) в виде теплового шума. Источник этой помехи находится в элементах самой приемной радиоаппаратуры, в частности, во входной цепи усилителя. В диапазоне звуковых частот и радиочастот спектральную плотность мощности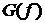 
теплового шума на омическом сопротивлении 
можно определить по формуле Найквиста [3].
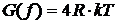(1),
где – омическое сопротивление;
- постоянная Больцмана;
, соответствует 
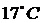принятой стандартной температуре
среды, в которой находится приемная аппаратура.
При этом
(2).
Поскольку усилитель усиливает не только ИС, но и помеху, тогда спектральная плотность мощности флуктуационной помехи на входе демодулятора будет существенно больше, чем на входе усилителя.
В КР АФП на входе демодулятора обозначена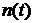 
, а ее спектральная плотность мощности 
обозначена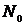 
. В КР в зависимости от номера варианта 
значение параметра 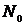задается в таблице 1 исходных данных.
Итак, на вход когерентного демодулятора поступает сигнал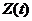 
равный
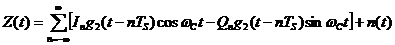(3),
где - первое слагаемое (сумма) является информационным сигналом квадратурной амплитудной модуляции КАМ-16,
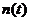- сигнал АФП.
В условиях действия флуктуационной помехи 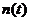демодулятор должен обеспечить оптимальные оценки 
и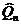 
передаваемых ИС 
и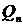 
на каждом символьном интервале 
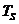с номером 
. Передаваемые ИС и 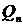на любом интервале с номером являются случайными величинами и принимают дискретные значения
(4),
с вероятностью 0,25 каждое.
Чтобы обосновать структурную схему когерентного демодулятора вначале предположим, что на вход демодулятора поступает не весь информационный сигнал (ИС) (3), а только его часть равная
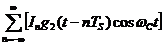(5).
Сигнал (5) – это сигнал обычной амплитудной модуляции (АМ). Выражение (5) задает ИС на всей оси времени 
на интервалах от 
до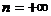 
.
На интервале с номером 
только одно слагаемое из выражения (5) будет отличаться от нулевого значения, а именно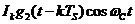 
, которому соответствует номер 
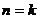. Остальные слагаемые из (5) на интервале от до 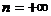будут равны нулю. Это объясняется формой импульсов 
для разных значений в (5), изображенных на рис. 4 б П4 к блоку ФМС».
В выражении (5) символы на любом интервале с номером 
принимают четыре равновероятных значений, указанных в (4) - .
Этим значениям (4) на интервале, например, с номером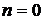 
будут соответствовать сигналы
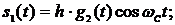
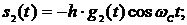
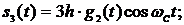
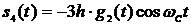(6).