Приложение к блоку «Декодер»(ДК) 6 глава

Обозначим энергии этих сигналов, соответственно, , величины энергий которых определяются по формуле , 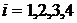. Из этой формулы и из равенств (6) следует, что

(7).

Каждый из сигналов (5) передает одно из 4-х возможных значений символа 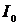. Из равенств (5) также следует, что сигналы элементарно выражаются через сигнал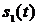

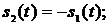
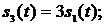
; (8).

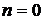Если ИС (5) рассматривать только в пределах одного интервала длительностью , например, с номером , то этот сигнал будет равен одному из 4-х возможных значений , где 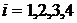задаются выражениями (6).

Известно из литературы [1,2], что алгоритм работы когерентного демодулятора, на вход которого поступает сигнал 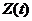равный

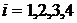, (9),

определяется выражением

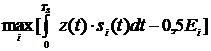(10).

В момент окончания символьного интервала длительностью демодулятор принимает решение в пользу того сигнала , которому соответствует максимальное значение квадратной скобки в (10).

Напряжение, равное значению интеграла в (10) можно сформировать на выходе активного фильтра (АФ) (коррелятора) или на выходе согласованного фильтра (СФ) с сигналом .

Принимаемые демодулятором решения в соответствии с (10) будут оптимальными в условиях действия флуктуационной помехи 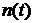типа белого шума. Учитывая выражения (6), (7), (8) реализация правила принятия решения в (10) может быть обеспечена структурной схемой демодулятора рис. 1.

 

Рис. 1 Структурная схема, реализующая выполнение алгоритма (10)

когерентного демодулятора.

Например, если решение будет принято в пользу сигнала 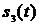, то это решение будет означать, что на данном интервале с номером 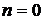согласно (6) значение символа .

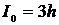Генератор вырабатывает сигнал на интервале с номером , а на интервале с номером сигнал .

На выходе интегратора в момент окончания символьного интервала длительностью будет сформировано напряжение равное интегралу

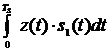. Это напряжение одновременно поступает на вход верхнего вычитающего устройства и на входы блоков, осуществляющих умножение на (-1) и на 3. На выходе верхнего вычитающего устройства получим напряжение равное разности

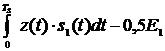(11).

На выходах блоков, осуществляющих умножение на (-1) и на 3, получим напряжения и . Используя (8) эти интегралы можно представить в виде

= ; = (12).

На выходе нижнего блока, осуществляющего умножение на (-1), получим напряжение , которое на основе равенств (8) можно представить как

(13).

Напряжения правых частей равенств (12) и (13) поступают на входы соответствующих вычитающих устройств, на выходах которых получим напряжения

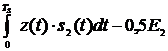; ; (14).

В момент окончания символьного интервала длительностью 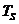решающее устройство (РУ1) сравнивает 4-е входных напряжения равенств (11), (14) и выбирает из них максимальное, тем самым реализуя правило

принятия решения (10).

Этот выбор определяет тот информационный сигнал из 4-х возможных сигналов, задаваемых равенством (6), который на данном символьном интервале поступил на вход демодулятора в составе сигнала 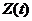, определяемого (9). Каждому сигналу из (6) соответствует определенное значение информационного символа 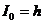, , или .

Таким образом, выбирая сигнал , демодулятор тем самым определяет значение передаваемого информационного символа 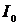из 4-х возможных ИС, то есть осуществляет оценку символа 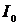. Произведенную оценку символа 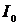обозначим . При правильном решении = 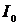. При ошибочном решении . Причиной ошибочных решений является действие помехи .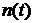

После принятия решения выходные цепи РУ1 генерируют прямоугольный импульс 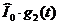длительностью с амплитудой , равной оценке значения передаваемого информационного символа , который может принимать одно из четырех значений . Импульс 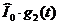появляется на выходе РУ1. Тогда при правильных оценках на выходе РУ1 появляется последовательность прямоугольных импульсов, соответствующая последовательности прямоугольных импульсов на верхнем выходе блока ФМС в передающем устройстве (см. рис. 4 в к блоку ФМС).

Теперь предположим, что по каналу связи вместо ИС (5) передается информационный сигнал, соответствующий второму слагаемому в сумме выражения (3).

(15).

По аналогии с сигналами (6) с учетом знака минус перед суммой в (15), введем сигналы на интервале с номером

.

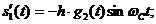
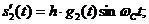
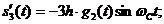
С помощью этих сигналов передаются 4-е значения символа 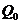на интервале с номером . Повторяя рассуждения, приведенные выше для получения схемы демодулятора рис. 1, получим схему демодулятора рис. 2.

Представлена схема рис. 2 демодулятора, осуществляющего оптимальные оценки значений передаваемых информационных символов в выражении (15), идентичной схеме рис. 1, но генератор 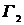в составе активного фильтра в схеме (рис. 2) на интервале с номером должен вырабатывать сигнал , а на интервале с номером , соответственно, сигнал .

Рис. 2 Схема демодулятора, когда на входе ИС (15).

Если на вход демодуляторов рис. 1 и рис. 2 подать сумму сигналов (5) и (15), то есть сигнал квадратурной модуляции (3), то это не отразится на работе обоих демодуляторов.

Действительно, пусть на вход демодулятора, (например, на рис. 1) поступает сигнал 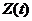, определяемый выражением (3), информационная часть которого является сигналом квадратурной АМ

(16).

На первый вход перемножителя из состава суммы (16) на интервале длительностью 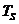с номером будет поступать сигнал равный только одному слагаемому из суммы (16), а именно номер которого равен нулю, то есть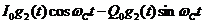

Остальные слагаемые в (16) на этом интервале будут равны нулю *).

На второй вход перемножителя от генератора на этом же интервале поступает сигнал . На выходе перемножителя получим произведение

[ ] .

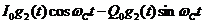В момент окончания символьного интервала, когда , на выходе интегратора будет формироваться напряжение

.

Первый интеграл является скалярным произведением сигналов

и , второй интеграл – скалярным произведением сигналов и . Так как на интервале интегрирования ,

то на выходе интегратора напряжение будет равно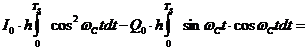

Учитывая, что и , после элементарных преобразований получим

(*).

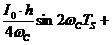
Третье слагаемое в сумме (*) получено из второго интеграла, то есть равно скалярному произведению сигналов и .

Поскольку частота 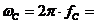, где - период гармонического сигнала с частотой , тогда третье слагаемое в (*) получим в виде . При этом частоту необходимо выбрать так, чтобы на символьном интервале длительностью укладывалось целое число периодов , то есть

(17).

 

--------------------------------------------------------------------------------------------

*)Это объясняется формой импульсов при (см. графики).

 

Причем 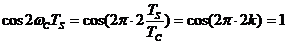и скалярное произведение сигналов и будет равно нулю, то есть 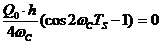. Это означает, что на интервале длительностью 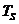эти сигналы ортогональны и находятся в квадратуре. Равенство (17) является условием ортогональности. Из условия ортогональности указанных сигналов следует самое существенное - напряжение, создаваемое сигналом на входе демодулятора, не оказывает влияния на решение, выносимое РУ1 в составе демодулятора. Так как в момент принятия решения, когда , напряжение, создаваемое сигналом на выходе интегратора, будет равно нулю и поэтому не зависит от величины информационного символа .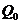

При выполнении условия ортогональности (17) второе слагаемое в сумме (*) также имеет нулевое значение, так как (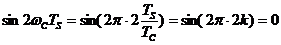) и на выходе интегратора будет напряжение равное , которое определяется только величиной передаваемого информационного символа .

Итак, при поступлении сигнала (16) на рис. 1 на вход демодулятора, РУ1 будет реагировать только на те слагаемые из (16), в состав которых входят символы , и не будет реагировать на слагаемые из (16), в состав которых входят символы .

Аналогично, при поступлении сигнала (16) на рис. 2 на вход демодулятора РУ2 будет реагировать только на те слагаемые в (16), в состав которых входят символы , и не будет реагировать на слагаемые из (16), в состав которых входят символы . Поэтому схемы демодуляторов рис. 1 и рис. 2 можно объединить в одну схему.

Учтено следующее обстоятельство. Генератор на интервале с номером вырабатывает напряжение , на интервале с номером , соответственно, напряжение 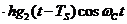и т.д. Когда заканчивается импульс в момент времени , то его продолжением будет импульс , а продолжением будет импульс и т.д. Поскольку амплитуда любого импульса равна 1 , то фактически генератор должен вырабатывать непрерывный гармонический сигнал .

Аналогично, генератор 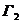должен вырабатывать второй непрерывный гармонический сигнал , который можно получить из сигнала при использовании фазовращателя и инвертора, изменяющего знак входного сигнала.

С учетом данного замечания возможная полная схема демодулятора для приема сигнала КАМ-16 изображена на рис. 3.

Рис. 3 Схема демодулятора для сигнала квадратурной модуляции КАМ-16.

 

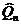Решающие устройства РУ1 и РУ2 осуществляют оценки и передаваемых модулирующих символов и . Если демодулятор работает без ошибок, то и , на выходах РУ1, РУ2 формируются сигналы, соответствующие сигналам на выходе блока ФМС (рис. 4 в «П4 блок ФМС»), и далее эти сигналы поступают на вход преобразователя параллельного кода в последовательный код. На выходе этого преобразователя формируется сигнал, соответствующий сигналу, который в передающем устройстве поступал на вход блока ФМС (рис. 4 в «П4 блок ФМС»).

Отметим, что вместо активных фильтров АФ1 и АФ2 в схемах демодуляторов рис. 1 и рис. 2 можно использовать согласованные фильтры СФ1 и СФ2 с сигналами и , соответственно.

 

ВЕРОЯТНОСТЬ ошибок на выходах РУ1 и РУ2

и вероятность ошибки на выходе преобразователя параллельного кода в последовательный код.

 

Рассмотренный ранее сигнал 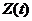, определенный выражением (3) на символьном интервале с номером , будет равен

(18)

1. Пусть значения переданных информационных символов (ИС) равны

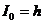; (19).

Тогда напряжения на входах РУ1 (рис. 1) в момент окончания символьного интервала длительностью будут, соответственно, равны в (11) и (14)

; ;

; .

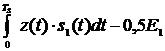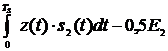Используя (14),(18),(19),(6) и (7) получим соответствующие напряжения на входах РУ1

;

;

;

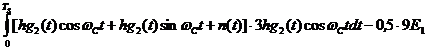. (20)

При дальнейших преобразованиях интегралов в (20), получим интегралы

и 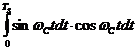, которые после использования равенства (17) будут равны

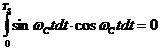; (21)

Получим напряжения на соответствующих входах РУ1 из выражения (20), используя (21).

На 1-м входе ; на 2-м входе ;

на 3-м входе ; на 4-м входе - 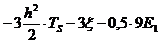(22),

где .

Принимая во внимание, что на интервале интегрирования импульс равен 1(В), получим

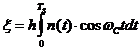. (23)

Так как 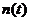- гауссовская флуктуационная помеха типа белого шума, то из (23) следует, что - гауссовская случайная величина. Вероятностные параметры случайной величины будут определены позднее.

Случайная величина в (22) является причиной ошибок, иногда происходящих в работе РУ1. Чем больше будет дисперсия случайной величины , тем чаще будут происходить ошибки.

При при правильных решениях РУ1 наибольшие напряжения будут формироваться, соответственно, на 1-м, 2-м,3-м или 4-м входах РУ1.

Если значение символа 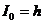по (19), тогда наибольшее напряжение при правильном решении будет на 1-м входе РУ1 и поэтому будут выполняться три неравенства в соответствии с (22)

> ;

> ;

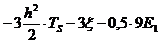> . (24), преобразуем (24) к виду

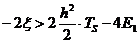; ; . (25).

После элементарных преобразований из (25) получим

; ; (26),

где - энергия сигнала .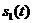

Используя (6), получим .