 Пример 1. К резервуару (рис. 1.11) заполненному бензином плотностью
Пример 1. К резервуару (рис. 1.11) заполненному бензином плотностью  =700
=700  , присоединен U-образный ртутный манометр, показание которого
, присоединен U-образный ртутный манометр, показание которого 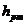 =0,1 м; уровень масла над ртутью
=0,1 м; уровень масла над ртутью  =0,2 м.
=0,2 м.
Определить абсолютное давление  паров на
паров на
|
манометра (обозначен буквой M), установленного на крышке резервуара, а также возможную высоту уровня бензина в пьезометре  при условии, что
при условии, что  =0,75 м; a=0,15 м; H=1,1 м; принять плотность масла
=0,75 м; a=0,15 м; H=1,1 м; принять плотность масла  900
900  ; плотность ртути
; плотность ртути  13,6
13,6 
 .
.
Решение.
Решение проведем с учетом атмосферного давления, поскольку по условию задачи необходимо определить абсолютное давление паров бензина.
Для решения задачи воспользуемся понятием плоскости уровня. Выберем плоскость уровня 0-0 на разделе жидкостей бензин-ртуть и составим условие равенства давления, приравняв давления в правом (p1) и левом (p2) колене u-образного манометра:
 ;
;
 ;
;
 .
.
Приравнивая давления получаем
 ,
,
отсюда абсолютное давление паров бензина:
 .
.
Принимая атмосферное давление  кПа, получаем:
кПа, получаем:

Показания манометра, установленного на крышке бака, определяется так:
 кПа =
кПа =
=0,089 ат.
Для определения возможной высоты бензина в пьезометрической трубке  составим условие равновесия жидкости относительно плоскости уровня 0-0, в этом случае расчеты можно вести по избыточному (манометрическому) давлению. Для плоскости уровня 0-0 запишем равенство давлений
составим условие равновесия жидкости относительно плоскости уровня 0-0, в этом случае расчеты можно вести по избыточному (манометрическому) давлению. Для плоскости уровня 0-0 запишем равенство давлений
 ,
,
отсюда
 м.
м.
Ответ.  =
=  Па;
Па;  ;
;  .
.
Пример 2. Два резервуара заполнены водой и бензином, линии центров которых находятся на одном уровне, соединены двухколенным ртутным манометром (рис. 1.12). Пространство между уровнями ртути в манометре заполнено маслом плотностью  900
900  .
.
Определить, в каком резервуаре давление больше и на какую величину если высоты уровней жидкостей равны соответственно:  =250 мм;
=250 мм;  =120 мм;
=120 мм;  =80 мм;
=80 мм;  =50 мм. Принять плотность бензина
=50 мм. Принять плотность бензина  720
720  ; ртути
; ртути  13,6
13,6 
 .
.

Решение.
Резервуары закрыты, следовательно давление будем рассчитывать по избыточному давлению без учета атмосферного давления. Обозначим давление на уровне центра в левом резервуаре  , в правом
, в правом  .
.
Определим положение плоскостей уровня для данной равновесной системы: это плоскости 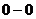 ,
,  ,
, 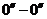 . Данные горизонтальные плоскости проводятся по однородной жидкости
. Данные горизонтальные плоскости проводятся по однородной жидкости 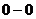 - по маслу, остальные по ртути. Для этих плоскостей запишем условие равенства давлений:
- по маслу, остальные по ртути. Для этих плоскостей запишем условие равенства давлений:  ;
;  ;
;  . Плоскость
. Плоскость 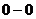 является основной плоскостью равновесного состояния для которой
является основной плоскостью равновесного состояния для которой  .
.
Согласно основному уравнению гидростатики, чтобы записать давление  , нужно к давлению в центре резервуара A (
, нужно к давлению в центре резервуара A ( ) прибавить давление столба воды
) прибавить давление столба воды  - получим давление
- получим давление  , из давления
, из давления  вычтем давление столба ртути
вычтем давление столба ртути  и, таким образом, получаем:
и, таким образом, получаем:
 .
.
Аналогично для давления  :
:
 .
.
Согласно чертежу, высота столба бензина
 .
.
По распределению ртути в дифференциальном манометре предположим, что давление в резервуаре A больше чем в резервуаре B. Найдем эту разность:
 .
.
Подставляя численные значения получаем 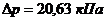 .
.
Ответ. 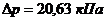 . Поскольку ответ положителен, то давление в резервуаре A больше чем в резервуаре B.
. Поскольку ответ положителен, то давление в резервуаре A больше чем в резервуаре B.
Пример 3. Определить какое давление – манометрическое или вакуум показывает мановакуумметр ( ), установленный по оси резервуара B с керосином, если показания манометра по центру резервуара A с водой
), установленный по оси резервуара B с керосином, если показания манометра по центру резервуара A с водой 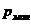 =0,12 ат. Между резервуарами подключен U-образный ртутный манометр, показание которого
=0,12 ат. Между резервуарами подключен U-образный ртутный манометр, показание которого 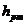 =200 мм; расстояние от уровня ртути в левом колене до оси резервуара A
=200 мм; расстояние от уровня ртути в левом колене до оси резервуара A  =300 мм. Оси центов резервуаров находятся на одной линии (рис. 1.13). Принять плотность керосина
=300 мм. Оси центов резервуаров находятся на одной линии (рис. 1.13). Принять плотность керосина 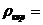 820
820  ; ртути
; ртути  13,6
13,6 
 .
.
Решение.
В данной задаче основной плоскостью уровня для всей системы является плоскость 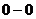 , в левой части она проходит по воде, в правой – по ртути U-образного манометра. Для этой плоскости
, в левой части она проходит по воде, в правой – по ртути U-образного манометра. Для этой плоскости  . В плоскости
. В плоскости  , проведенной в керосина
, проведенной в керосина  . Задача решается без учета атмосферного давления. Если рассчитанное давление на уровне установки мановакуумметра (МВ) получится положительным, то прибор работает как манометр, в противном случае как вакууметр.
. Задача решается без учета атмосферного давления. Если рассчитанное давление на уровне установки мановакуумметра (МВ) получится положительным, то прибор работает как манометр, в противном случае как вакууметр.
 |
Запишем давление на уровне установки мановакуумметра. Имеем манометрическое давление 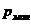 по оси резервуара A, поднимаемся до плоскости уровня
по оси резервуара A, поднимаемся до плоскости уровня 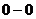 , т.е. вычитаем давление столба воды
, т.е. вычитаем давление столба воды  , получаем давление
, получаем давление  , по плоскости уровня переходим в левое колено U-образного манометра, где
, по плоскости уровня переходим в левое колено U-образного манометра, где  . Затем переходим в правое крыло манометра, где
. Затем переходим в правое крыло манометра, где  , поднимаемся к плоскости
, поднимаемся к плоскости  , т.е. вычитаем давление столба ртути
, т.е. вычитаем давление столба ртути  и получаем давление
и получаем давление  ; переходим по плоскости уровня
; переходим по плоскости уровня  к давлению
к давлению  . К полученному давлению
. К полученному давлению 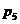 прибавляем давление столба керосина
прибавляем давление столба керосина  поскольку опускаемся вниз до оси резервуара B.
поскольку опускаемся вниз до оси резервуара B.
Таким образом

Подставляя числовые значения получаем


Знак «минус» говорит о том, что мановакуумметр работает как вакуумметр.
Ответ. Мановакуумметр работает как вакуумметр и показывает вакуумметрическое давление 
Тема № 2. «Сила давления жидкости на плоские поверхности».
 Задание 1. Патрубок резервуара перекрывается круглой крышкой, поворачивающейся вокруг шарнира A. Определить каким должно быть показание U-образной трубки, заполненной ртутью (
Задание 1. Патрубок резервуара перекрывается круглой крышкой, поворачивающейся вокруг шарнира A. Определить каким должно быть показание U-образной трубки, заполненной ртутью (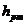 ), установленного на поверхности масла, чтобы крышка находилась в закрытом
), установленного на поверхности масла, чтобы крышка находилась в закрытом
положении за счет вакуума
(рис. 2.1). Принять: диаметр крышки - D, глубину масла до шарнира A – h, плотность масла  , плотность ртути
, плотность ртути  . Числовые данные берутся из таблицы 2.
. Числовые данные берутся из таблицы 2.
 Задание 2. В вертикальной перегородке отстойника состоящего из двух резервуаров – A и B, проделано квадратное отверстие со стороной a, которое перекрывается крышкой, поворачивающейся вокруг шарнира O. Определить, какой наименьший вакуум нужно создать на поверхности воды в закрытом резервуаре A, чтобы
Задание 2. В вертикальной перегородке отстойника состоящего из двух резервуаров – A и B, проделано квадратное отверстие со стороной a, которое перекрывается крышкой, поворачивающейся вокруг шарнира O. Определить, какой наименьший вакуум нужно создать на поверхности воды в закрытом резервуаре A, чтобы
крышка оставалась в закрытом положении. Резервуар B открыт (рис. 2.2). Числовые данные берутся из таблицы 2.
 Задание 3. Определить величину и направление силы N, приложенной к штоку гидроцилиндра для удержания его на месте, если показание мановакуумметра равно
Задание 3. Определить величину и направление силы N, приложенной к штоку гидроцилиндра для удержания его на месте, если показание мановакуумметра равно  . Гидроцилиндр заполнен маслом протностью
. Гидроцилиндр заполнен маслом протностью  , диаметр поршня d, высота уровня масла
, диаметр поршня d, высота уровня масла
на уровне оси поршня H (рис. 2.3). Числовые данные берутся из таблицы 2.
 Задание 4. Определить силу давления бензина на треугольный затвор шириной b и высотой h, а также положение центра давления, если показание манометра установленного на расстоянии a от верхней кромки затвора равно
Задание 4. Определить силу давления бензина на треугольный затвор шириной b и высотой h, а также положение центра давления, если показание манометра установленного на расстоянии a от верхней кромки затвора равно 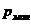 (рис. 2.4). Принять плотность бензина
(рис. 2.4). Принять плотность бензина  . Числовые данные берутся из таблицы 2.
. Числовые данные берутся из таблицы 2.
 Задание 5. Определить величину и положение равнодействующей сил давления воды на плоскую ломаную стенку ABC, удерживающую слева напор воды H, справа h. Длина стенки в плоскости, перпенди-кулярной плоскости чертежа L. Верхняя часть стенки
Задание 5. Определить величину и положение равнодействующей сил давления воды на плоскую ломаную стенку ABC, удерживающую слева напор воды H, справа h. Длина стенки в плоскости, перпенди-кулярной плоскости чертежа L. Верхняя часть стенки
|
 к горизонту (рис. 2.5). Расчет
к горизонту (рис. 2.5). Расчет
выполнить графо-аналитическим методом. Числовые данные берутся из таблицы 2.
 Задание 6. Определить нормальное усилие F, приложенное к наклонной крышке AB для удержания крышки в закрытом положении. Крышка расположена под углом
Задание 6. Определить нормальное усилие F, приложенное к наклонной крышке AB для удержания крышки в закрытом положении. Крышка расположена под углом  к горизонту и укреплена с помощью шарнира B и перекрывает патрубок квадратного сечения со
к горизонту и укреплена с помощью шарнира B и перекрывает патрубок квадратного сечения со
стороной a. Патрубок заполнен маслом плотностью  . К дну патрубка присоединен пьезометр показание которого H. Сила F приложена на расстоянии b =50 мм от стенки патрубка (рис. 2.6). Числовые данные берутся из таблицы 2.
. К дну патрубка присоединен пьезометр показание которого H. Сила F приложена на расстоянии b =50 мм от стенки патрубка (рис. 2.6). Числовые данные берутся из таблицы 2.
Задание 7. Патрубок маслобака квадратного сечения со стороной a перекрывается крышкой AB, перемещающейся в вертикальных пазах. Определить силу F для открытия крышки, если показания манометра установленного на верхней стенке патрубка 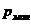 . Принять плотность масла
. Принять плотность масла  =900
=900

 , коэффициент трения скольжения в пазах - f. Масса крышки M =2,0 кг (рис. 2.7). Числовые данные берутся из таблицы 2.
, коэффициент трения скольжения в пазах - f. Масса крышки M =2,0 кг (рис. 2.7). Числовые данные берутся из таблицы 2.

|
 . Принять показание манометра на поверхности воды
. Принять показание манометра на поверхности воды 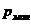 , глубину заполнения резервуара H, массу крышки M = 4,0 кг.
, глубину заполнения резервуара H, массу крышки M = 4,0 кг.
Трением в шарнире и направляющих троса пренебречь (Рис. 2.8). Числовые данные берутся из таблицы 2.
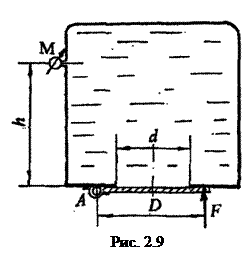 Задание 9. Закрытый резервуар, заполненный водой находится под давлением. В резервуаре круглое отверстие диаметром d, закрывается крышкой D, закрепленной шарниром в точке A. Определить силу F удерживающую крышку в закрытом положении, если масса крышки M = 4,0 кг. Показание манометра на расстоянии h от дна равны
Задание 9. Закрытый резервуар, заполненный водой находится под давлением. В резервуаре круглое отверстие диаметром d, закрывается крышкой D, закрепленной шарниром в точке A. Определить силу F удерживающую крышку в закрытом положении, если масса крышки M = 4,0 кг. Показание манометра на расстоянии h от дна равны 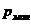 (рис. 2.9). Числовые данные берутся из таблицы 2.
(рис. 2.9). Числовые данные берутся из таблицы 2.
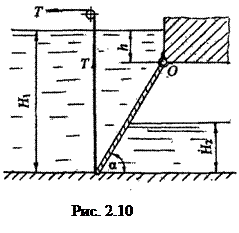 Задание 10. Определить усилие T, которое нужно приложить к вертикальному тросу для открытия щита, перекрывающего канал прямоугольного сечения. Щит расположен под углом
Задание 10. Определить усилие T, которое нужно приложить к вертикальному тросу для открытия щита, перекрывающего канал прямоугольного сечения. Щит расположен под углом  =60
=60  к горизонту и закреплен шарнирно в т. O к опоре. Ширина щита в плоскости, перпендикулярной плоскости чертежа B =3,0 м. Глубина воды перед щитом
к горизонту и закреплен шарнирно в т. O к опоре. Ширина щита в плоскости, перпендикулярной плоскости чертежа B =3,0 м. Глубина воды перед щитом  , за щитом
, за щитом  .
.
Уровень воды над шарниром h. Масса щита M=500 кг (рис. 2.10). Задание выполнить графо-аналитическим способом. Требуемые данные берутся из таблицы 2.
Таблица 2.
| Величины | Последняя цифра зачетной книжки | ||||||||||
| D, мм | |||||||||||
| h, мм | |||||||||||
| a, мм | |||||||||||
 , м , м
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | |
 , м , м
| 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | |
 , ат , ат
| -0,1 | 0,1 | -0,11 | 0,11 | -0,12 | 0,12 | -0,13 | 0,13 | -0,14 | 0,14 | |
| d, мм | |||||||||||
| H, м | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | |
| b, мм | |||||||||||
| h, мм | |||||||||||
| a, мм | |||||||||||
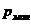 , ат , ат
| 0,07 | 0,08 | 0,09 | 0,10 | 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,16 | |
| H, м | 4,0 | 4,2 | 4,4 | 4,6 | 4,8 | 5,0 | 5,2 | 5,4 | 5,6 | 5,8 | |
| h, м | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | |
| L, м | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | |
 , град , град
| |||||||||||
 , град , град
| |||||||||||
| a, мм | |||||||||||
| H, мм | |||||||||||
| a, мм | |||||||||||
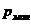 , ат , ат
| 0,08 | 0,09 | 0,1 | 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,16 | 0,17 | |
| f | 0,7 | 0,65 | 0,6 | 0,55 | 0,5 | 0,45 | 0,4 | 0,35 | 0,3 | 0,25 | |
| D, мм | |||||||||||
 , град , град
| |||||||||||
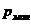 , ат , ат
| 0,08 | 0,09 | 0,10 | 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,16 | 0,17 | |
| d, мм | |||||||||||
| D, мм | |||||||||||
| h, м | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | |
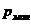 , ат , ат
| 0,21 | 0,22 | 0,23 | 0,24 | 0,25 | 0,26 | 0,27 | 0,28 | 0,29 | 0,30 | |
 , м , м
| 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | |
 , м , м
| 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | |
| h, м | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |