Пример 1. Цилиндрический затвор диаметром D = 0.6 м перекрывает прямоугольное отверстие в вертикальной стенке, удерживающей напор воды. Высота отверстия равна диаметру затвора, длина отверстия L = 0,2 м. Уровень воды над верхней кромкой затвора h = 0,2 м. Затвор может поворачиваться относительно горизонтальной оси и, перемещаясь, открывать отверстие (рис. 3.11).
Определить величину и угол наклона к горизонту силы давления воды на цилиндрический затвор.
Решение.
На рис. 3.11а показан общий вид затвора. Решение представим в плоском чертеже для вертикального сечения затвора, при этом длина затвора L перпендикулярна плоскости чертежа (рис. 3.11б). Решение проведем по следующей методике.
1. Выберем два направления x и y по которым определяем составляющие давления жидкости. При этом сила полного давления 
. Для данной цилиндрической поверхности достаточно двух направлений, поскольку она имеет ось симметрии.
Начало координат выбираем на свободной поверхности. Ось y направляем вертикально вниз, так как положительное направление значения глубины отсчитывается от свободной поверхности вниз. Ось x направляем по свободной поверхности вправо по направлению действия жидкости (рис. 3.11б).
2. Определяем горизонтальную составляющую 
.
Криволинейную поверхность AB спроектируем внутрь жидкости на вертикальную плоскость. Получим вертикальную проекцию 
представляющую собой прямоугольник высотой D и шириной L (рис. 3.11в). Рассчитаем силу давления воды на данную вертикальную проекцию.
Площадь вертикальной проекции Ay=DL. Глубина погружения центра тяжести C данной проекции yc = h+D/2 = 0,5 м. Покажем на чертеже yc. Рассчитаем горизонтальную составляющую Rx = rg(h+D/2)DL = 103×9,8×0,5×0,6×2,0 = 5,88×103 = 5,88 кН.
Определяем глубину погружения центра давления yD для горизонтальной составляющей (глубину точки приложения силы Rx) 
, где 
- центральный момент инерции относительно горизонтальной оси для вертикальной проекции криволинейной поверхности. При этом 
.
После подстановки данных получаем
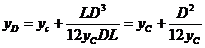; эксцентриситет 
;
; 
.
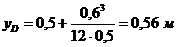Указываем на чертеже yD, эксцентриситет e и положение силы Rx.
Горизонтальную составляющую Rx также можно определить графо-аналитическим методом: 
.
Определим давление воды в точках 
и 
:
.
.
Построим эпюру гидростатического давления (рис. 3.11в). Эпюра представляет собой призму с основанием в виде трапеции высотой L, тогда
.
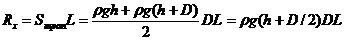Графически находим положение центра давления. Глубина погружения центра давления совпадает с положением центра тяжести эпюры в виде трапеции (рис. 3.11в). Находим координату центра тяжести эпюры
.
Центр тяжести трапеции можно также определить геометрическим построением.
На рис. 3.11в указываем yц.т.эп., получим yD=h+D- yц.т.эп.=0,56 м.
3. Определяем вертикальную составляющую Ry силы давления воды на цилиндрическую поверхность Ry=rgVт.д.
Криволинейна поверхность имеет две части – AC и CB.
Строим тело давления для части AC. Из контура криволинейной части AC проводим вертикальные линии до свободной поверхности жидкости, получим реальное (положительное) тело давления в виде криволинейной призмы с основанием AKMC, построенное на смоченной поверхности AC и заполненное водой. В эпюре тела давления стрелки направляем вниз.
Для части криволинейной поверхности CB проведем вертикальные линии до свободной поверхности; получим отрицательное тело давления в виде криволинейной призмы с основанием BCMK, поскольку оно построено на несмоченной поверхности и не заполнено жидкостью. Стрелки в эпюре тела давления показаны пунктирно и направлены вверх.
Анализ построения двух давлений показывает, что в объеме AKMC два тела давления взаимно компенсируются.
Результирующее тело давления отрицательно в виде полуцилиндра объемом 
.
Вертикальная составляющая Ry:
.
Показываем линию действия и точку приложения Ry. Вертикальная составляющая приложена в центре тяжести тела давления и направлена вверх. Центр тяжести полуцилиндра находится на расстоянии 
от оси цилиндра.
На чертеже указываем расстояние xC, центр тяжести полуцилиндра и направление силы Ry.
4. Определяем величину равнодействующей давления воды на цилиндрический затвор 
.
Чтобы найти линию действия, направление и точку приложения равнодействующей R, по линии действия продолжим Rx и Ry до взаимного пересечения, получим точку N. Геометрическое сложение сил проведем вне чертежа. Вынесем точку N и покажем сложение сил в масштабе.
Параллельно по линии действия силу R перенесем в точку N на основном чертеже и продолжим ее до пересечения с криволинейной поверхностью. Равнодействующая R должна пройти через точку пересечения составляющих и центр криволинейной поверхности.
Точка пересечения равнодействующей с цилиндрической поверхностью является центром давления.
Угол a наклона равнодействующей R найдем из уравнения 
, отсюда 
.
Ответ: равнодействующая давления воды R = 6,5 кН направлена радиально под углом .
Пример 2. Определить силу давления воды на четверть цилиндрической поверхности AB открытого резервуара, угол наклона силы к горизонту и глубину погружения центра давления, если глубина заполнения резервуара H = 1,6 м, радиус цилиндрической поверхности r = 0,8 м, длина резервуара L = 5,0 м (рис. 3.12).
Решение
На рис. 3.12а дан общий вид резервуара с цилиндрической поверхностью в изометрии. На рис. 3.12б представлено среднее сечение резервуара нормальной плоскостью.
Выбираем направления x и y, по которым определяются составляющие силы давления с последующим их геометрическим сложением 
.
Начало координат выбираем на свободной поверхности. Ось x направляем вправо по направлению действия жидкости, ось y – вертикально вниз.
Определяем горизонтальную составляющую . Спроектируем цилиндрическую поверхность AB на вертикальную плоскость. Получаем в проекции прямоугольник высотой AB = r и шириной равной длине резервуара L. Площадь вертикальной проекции четверти цилиндра Ay = rL.
Находим глубину погружения центра тяжести вертикальной проекции yC, которая отсчитывается от свободной поверхности жидкости 
. Показываем yC на чертеже (рис. 3.12б).
Рассчитываем горизонтальную составляющую
.
Показываем направление и точку приложения силы 
. Сила приложена в центре давления по нормали к вертикальной проекции AB` на глубине 
.
При этом 
. Здесь IC – центральный момент инерции вертикальной проекции криволинейной поверхности относительно горизонтальной оси, т.е. 
. Подставляя значения параметров получим
.
При этом эксцентриситет равен 
. На чертеже (рис. 3.12б) указываем координату центра давления , эксцентриситет e, направление и точку приложения силы .
Определяем вертикальную составляющую 
Вертикальная составляющая равна силе тяжести жидкости в объеме тела давления. Чтобы найти объем тела давления построим эпюру тела давления. Из контура цилиндрической поверхности проведем вертикальные линии до продолжения свободной поверхности. Тело давления ограничено самой криволинейной поверхностью AB, вертикальными проектирующими плоскостями и горизонтальной проекцией криволинейной поверхности AB на продолжение горизонта свободной поверхности.
Очерченное тело давления построено на несмоченной части криволинейной поверхности AB, не заполнено жидкостью, поэтому оно считается отрицательным. Стрелки в эпюре тела давления направлены вверх. Тело давления представляет криволинейную призму с основанием AA``B``B и высотой L.
Площадь основания тела давления можно рассматривать как разность площадей двух фигур: прямоугольника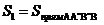 
и четверти круга 
. Тогда объем тела давления есть 
. Тогда
.
Определим направление и точку приложения Ry. Сила Ry из центра тяжести тела давления будет направлена вверх, поскольку тело давления отрицательно.
Положение центра тяжести составной фигуры определим, пользуясь понятием статического момента площади. Согласно курсу «Сопротивления материалов» в данной точке координаты центра тяжести сложной фигуры рассчитываются по формулам
; 
, где
- площадь прямоугольника AA``B``B;
- площадь четверти круга;
и 
, 
и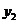 
- координаты центров тяжести прямоугольника и четверти круга относительно осей 
и 
.
На рис. 3.12в представлено основание тела давления AA``B``B. Временные оси и для удобства расчетов совпадают с направлением осей x и y на основном чертежа (рис. 3.12б).
Для расчета координат центра тяжест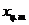и 
и 
фигуры AA``B``B имеем:
; 
; 
;
; 
;
.
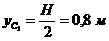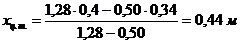Откладываем значения координат центра тяжести тела 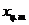и на рис. 3.12в, показываем положение центра тяжести тела давления. В масштабе переносим положение центра тяжести тела давления на основной чертеж и показываем линию действия и точку приложения вертикальной составляющей Ry.
Определим величину равнодействующей сил давления R на цилиндрическую поверхность AB 
кН.
Находим положение силы R. Геометрически сложим составляющие Rx и Ry: продолжим силы по линии действия до их взаимного пересечения, получим точку N, через которую проходит равнодействующая R.
Вынесем точку N за пределы чертежа и покажем сложение сил. Чтобы найти положение центра давления для равнодействующей R, силу R по линии действия параллельно перенесем в точку N на основной чертеж (рис. 3.12б) и продолжим ее до пересечения с криволинейной поверхностью AB.
Определим угол наклона равнодействующей к горизонту. При этом 
, отсюда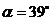 
.
Глубину погружения центра давления для равнодействующей R рассчитаем по формуле 
.
Показываем на основном чертеже глубину погружения центра давления для равнодействующей (рис. 3.6б).
Ответ: сила давления воды на цилиндрическую поверхность 
радиально направлена под углом 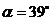, приложена на глубине 
.
Пример 3. Определить силу давления бензина на полусферическую крышку закрытого резервуара. На поверхности бензина действует избыточное давление паров бензина p ман = 0,03 ат. Крышка перекрывает круглое донное отверстие радиусом r = 0,3 м. Глубина заполнения резервуара H = 0,9 м. Принять плотность бензина rбенз = 750 кг/м3.
Решение.
На рис. 3.13а представлен общий вид резервуара с бензином в вертикальном разрезе.
Выберем следующий вариант решения: манометрическое давление на поверхности жидкости переводим в давление столба бензина, условно заменив манометр пьезометром, находим пьезометрическую высоту и положение условной свободной поверхности. Рассчитаем пьезометрический напор по показанию манометра
.
На уровне свободной поверхности в резервуаре (рис. 3.13б) пунктиром указывается пьезометр, высота столба жидкости в котором соответствует 
. По уровню жидкости в пьезометре указывается условная свободная поверхность, от которой отсчитываются координаты центров тяжести фигур и центра давления.
Дальнейший расчет проведем по следующей методике:
1. Выберем два направления x и y (рис. 3.13б) по которым определим составляющие силы давления с последующим их геометрическим сложением.
2. Определим горизонтальную составляющую 
.
Полусферическая поверхность AKB имеет две части: AK, на которую бензин действует слева и KB с действием бензина справа.
Чтобы определить горизонтальную силу на левую часть полусферы, спроектируем часть AK внутрь жидкости на вертикальную плоскость. В проекции получим полукруг площадью 
. Проекция показана пунктирными линиями.
Затем спроектируем правую часть полусферы внутрь жидкости и получим такую же проекцию в виде полукруга площадью 
.
Найдем координаты центров тяжести данных проекций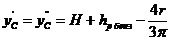 
. Указываем координаты центров тяжести на чертеже (рис. 3.13б).
Горизонтальные силы слева и справа имею вид
, 
. Данные силы равны по величине и противоположны по направлению. Поскольку равны координаты центров тяжести проекций, то равны и координаты центров давления справа и слева, т.е. 
. Таким образом, после геометрического сложения составляющих горизонтальной силы получим, что 
, т.е. горизонтальная составляющая силы давления жидкости на полусферическую поверхность равна нулю.
3. Определим вертикальную составляющую силы давления на полусферическую поверхность 
.
Для построения тела давления из контура полусферы проведем вертикальные линии до условной свободной поверхности. Получим эпюру тела давления. Тело давления построено на смоченной части полусферы и заполнено жидкостью, значит оно положительное (действительное). Стрелками направленными вниз указывается действие бензина на полусферическую крышку (сила Ry также направлена вниз).
Горизонтальная проекция полусферы на условную свободную поверхность представляет круг.
Таким образом, объем тела давления есть объем цилиндра высотой (H+hp бенз), за вычетом объема полусферы:
. Тогда вертикальная составляющая
.
Покажем линию действия и точку приложения вертикальной силы Ry. Линия действия силы совпадает с геометрической осью полусферической поверхности и цилиндра. Определим координату центра тяжести тела давления yу.т. Временную ось yвр. совместим с осью y, тогда
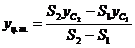, где
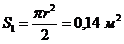- площадь полукруга (вертикального сечения полусферы);
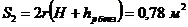- площадь прямоугольника;
- координата центра тяжести C1 полукруга;
- координата центра тяжести C2 прямоугольника.
Используя данные значения получим 
. Указываем на чертеже и положение центра тяжести тела давления.
Из цента тяжести тела давления вертикальную силу Ry направляем вниз. Поскольку горизонтальная сила равна нулю, на полусферическую поверхность действует только вертикальная сила.
Ответ: на полусферическую крышку резервуара по оси полусферы действует сила R = Ry = 2,29 кН.
Тема № 4. «Расчет простых трубопроводных систем».
Задание 1. При закрытом кране на трубопроводе диаметром d и длиной l показания манометра перед краном pман.
Определить показание манометра при открытом кране, если слив воды происходит в мерную емкость. За время t = 30 с наполняется объем W = 70,5 л. Труба водопроводная с абсолютной шероховатостью 
= 1,0 мм. Учесть потери напора на входе в трубу с острыми кромками. Принять коэффициент вязкости воды 
(рис. 4.1). Требуемые числовые значения берутся из таблицы 4.
 |
Задание 2. Из напорного бака с постоянным напором H вода подается в зумпф по двум трубам d1, l1 и d2, l2. Определить расход воды в трубопроводе и скорость движения воды в каждой трубе. На трубе диаметром d1 установлен пробковый кран с углом закрытия a = 40°. Учесть потери напора на входе в трубу с острыми кромками, а также при внезапном сужении (xв.с. = 0,38). Трубы водопроводные нормальные (рис. 4.2.). Требуемые числовые значения берутся из таблицы 4.
Задание 3. Из резервуара A в резервуар B вода передается по трубопроводу диаметром d, состоящему из трех участков длиной l1, l2, l3. Расход воды в системе равен Q. На входе в трубу установлена решетка без обратного клапана, на первом участке стоит вентиль с коэффициентом сопротивления xвент. = 5,0 (рис. 4.3).
Напор воды в резервуаре A H1 = 1,5 м, в резервуаре B – H2 = 2,5 м. Определить показание манометра (pман2) на поверхности воды в резервуаре B, если показание манометра на поверхности воды в резервуаре A pман1 = 0,45 ат. Принять абсолютную шероховатость трубы 
; кинематический коэффициент вязкости воды . Построить напорную и пьезометрическую линии. Требуемые числовые значения берутся из таблицы 4.
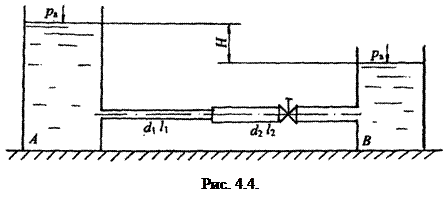
Задание 4. Определить расход воды из дозаторного резервуара A в резервуар B при постоянном напоре H, по трубам d1, l1 и d2, l2. Трубы водопроводные нормальные. На трубе d2 установлен пробковый кран с углом закрытия a = 40°.
Учесть потери напора на входе и выходе трубопроводной системы, а также при внезапном расширении трубопровода. Построить напорную и пьезометрическую линии, показать эпюру потерь напора (рис. 4.4). Требуемые числовые значения берутся из таблицы 4.
 |
Задание 5. С помощью насоса в напорный бак подается вода на высоту H, диаметр трубы h, длина l. Показание манометра в начале трубопровода pман1, в конце pман2. Определить при каком коэффициенте сопротивления пробкового крана будет обеспечен расход Q. Принять абсолютную шероховатость трубы D = 0,5 мм, коэффициент кинематической вязкости воды v = 10-6 м2/с (рис. 4.5). Требуемые числовые значения берутся из таблицы 4.
Задание 6. Бензин из бензохранилища с помощью насоса подается в бензобак на высоту H. На поверхности бензина в бензобаке поддерживается вакуум pвак. Определить, каким должно быть манометрическое давление (pман в ат) на выходе из насоса, при подаче Q, если транспортирование бензина
происходит по новой стальной трубе с абсолютной шероховатостью D = 0,05 мм, диаметром d, длиной l, на трубе установлена задвижка Лудло со степенью закрытия a/d = 5/8. Учесть потери напора в двух коленах и на выходе из трубы в бензобак. Принять плотность бензина rбенз = 720 кг/м3; коэффициент кинематической вязкости бензина 
(рис. 4.6). Требуемые числовые значения берутся из таблицы 4.
Задание 7. В пневмотраноспортной системе регулирование скорости и расхода воздуха осуществляется с помощью задвижки и контролируется по U – образному спиртовому мановакуумметру, установленному на входном участке коллектора. Определить каким должно быть показание мановакуумметра (hсп) на трубе диаметром d, при расходе воздуха Q. Принять коэффициент сопротивления на входе в коллектор xвх = 0,2; плотность воздуха rвозд = 1,22 кг/м3; плотность спирта rсп = 880 кг/м3 (рис. 4.7). Требуемые числовые значения берутся из таблицы 4.
Задание 8. В плотине сделан водоспуск в виде железобетонной трубы с весьма хорошей бетонировкой диаметром d и длиной l. Напор над водоспуском при истечении в атмосферу H. Определить пропускную способность трубы Q, если она имеет водозаборную сетку без обратного клапана.
Как изменится пропускная способность трубы, если за водосливом напор поднимется до h (рис. 4.8). Требуемые числовые значения берутся из таблицы 4.
 |
Задание 9. Определить показание U – образного спиртового манометра установленного на трубе Вентура в вентиляционном трубопроводе при значении диаметров d1 и d2, если расход воздуха равен Q. Принять плотность воздуха rвозд = 1,23 кг/м3; плотность спирта rсп = 820 кг/м3. Коэффициент сопротивления трубы Вентура принять равным xвент. = 0,2 (рис. 4.9). Требуемые числовые значения берутся из таблицы 4.
Задание 10. Для измерения расхода воды в трубопроводе диаметром d1 установлен расходометр Вентури с диаметром цилиндрической части d2. К широкой и узкой части расходометра подсоединены пьезометры в виде U – образной трубки, расстояние между которыми равно z. Пренебрегая потерями напора, определить скорости в широкой и узкой части трубы, а также расход воды в трубопроводе, если разность показаний пьезометров равна h. При расчете давлением столба воздуха в пьезометре пренебречь. Коэффициент Кориолиса принять равным единице (a = 1,0) (рис. 4.10)
Таблица 4.
| Величины | Последняя цифра зачетной книжки | ||||||||||
| d, мм | |||||||||||
| l, м | 8,5 | 9,5 | 10,5 | 11,5 | 12,5 | ||||||
| pман, ат | 0,16 | 0,165 | 0,17 | 0,175 | 0,18 | 0,185 | 0,19 | 0,195 | 0,2 | 0,205 | |
| H, м | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 | |
| d1, мм | |||||||||||
| l1, м | 4,3 | 4,4 | 4,6 | 4,8 | 5,0 | 5,3 | 5,6 | 5,9 | 6,2 | 6,5 | |
| d2, мм | |||||||||||
| l2, м | 7,6 | 7,7 | 7,8 | 7,9 | 8,0 | 8,1 | 8,2 | 8,3 | 8,5 | 8,7 | |
| d, мм | |||||||||||
| l1, м | 5,0 | 5,1 | 5,2 | 2,3 | 5,4 | 5,5 | 5,4 | 5,3 | 5,2 | 5,1 | |
| l2, м | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,4 | 4,3 | 4,2 | 4,1 | |
| l3, м | 6,0 | 6,1 | 6,2 | 6,3 | 6,4 | 6,4 | 6,3 | 6,2 | 6,1 | 6,0 | |
| Q, л/с | 2,5 | 2,6 | 2,7 | 2,5 | 2,6 | 2,7 | 2,5 | 2,6 | 2,7 | 2,6 | |
| H, м | 2,5 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 | 3,7 | 3,9 | 4,1 | 4,3 | |
| d1, мм | |||||||||||
| l1, м | 5,0 | 5,1 | 5,2 | 5,3 | 5,4 | 5,5 | 5,6 | 5,7 | 5,8 | 5,9 | |
| d2, мм | |||||||||||
| l2, м | 8,0 | 8,1 | 8,2 | 8,3 | 8,4 | 8,5 | 8,6 | 8,7 | 8,8 | 8,9 | |
| H, м | 5,2 | 5,4 | 5,6 | 5,8 | 6,0 | 6,2 | 6,4 | 6,6 | 6,8 | 7,0 | |
| d, мм | |||||||||||
| l, м | |||||||||||
| pман1, ат | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | |
| pман2, ат | 0,55 | 0,6 | 0,65 | 0,7 | 0,75 | 0,8 | 0,85 | 0,9 | 0,85 | 0,9 | |
| Q, л/с | 5,2 | 5,4 | 5,6 | 5,8 | 6,0 | 6,2 | 6,4 | 6,6 | 6,8 | 7,0 | |
| H, м | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 | 4,2 | 4,4 | 4,6 | 4,8 | |
| pвак, ат | 0,16 | 0,17 | 0,18 | 0,19 | 0,20 | 0,21 | 0,22 | 0,23 | 0,24 | 0,25 | |
| Q, л/с | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | |
| d, мм | |||||||||||
| l, м | |||||||||||
| d, мм | |||||||||||
| Q, л/с | |||||||||||
| d, мм | |||||||||||
| l, м | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | |
| H, м | 2,8 | 3,1 | 3,4 | 3,7 | 4,0 | 4,3 | 4,6 | 4,9 | 5,2 | 5,5 | |
| d1, мм | |||||||||||
| d2, мм | |||||||||||
| Q, л/с | 72,5 | 74,0 | 75,5 | 77,0 | 78,5 | 80,0 | 81,5 | 83,0 | 84,5 | 86,0 | |
| d1, мм | |||||||||||
| d2, мм | |||||||||||
| h, см |