ВВЕДЕНИЕ
Для расчёта на прочность, жёсткость и устойчивость элементов конструкций необходимо знать геометрические характеристики поперечных сечений. В большинстве случаев поперечные сечения брусьев имеют сложную форму. Поэтому нужно уметь определять геометрические характеристики сложных сечений.
В данной работе рассматривается сложное сечение, составленное из прямоугольника, двутавра и треугольника. Необходимо определить геометрические характеристики сложного сечения, используемые при расчётах элементов конструкций на прочность, жёсткость и устойчивость.
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОСТЫХ СОСТАВЛЯЮЩИХ СЛОЖНОГО СЕЧЕНИЯ
Геометрические характеристики прямоугольного сечения
Рисунок 1 – Сечение прямоугольник
Геометрические характеристики двутаврового сечения
Рисунок 2 – Двутавровое сечение
Геометрические характеристики треугольного профиля
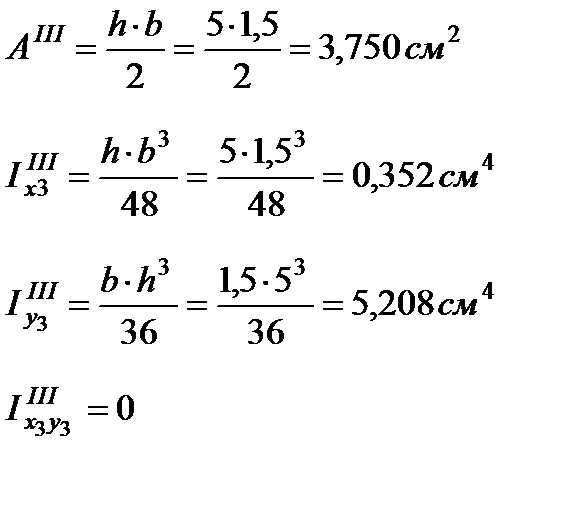
Рисунок 3 – Треугольник
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ СОСТАВНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНЫХ ОСЕЙ
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ВСЕГО СЕЧЕНИЯ ОТНОСИТЕЛЬНО ЦЕНТРАЛЬНЫХ ОСЕЙ
ОПРЕДЕЛЕНИЕ ГЛАВНЫХ МОМЕНТОВ ИНЕРЦИИ ВСЕГО СЕЧЕНИЯ И ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ АНАЛИТИЧЕСКИМ МЕТОДОМ
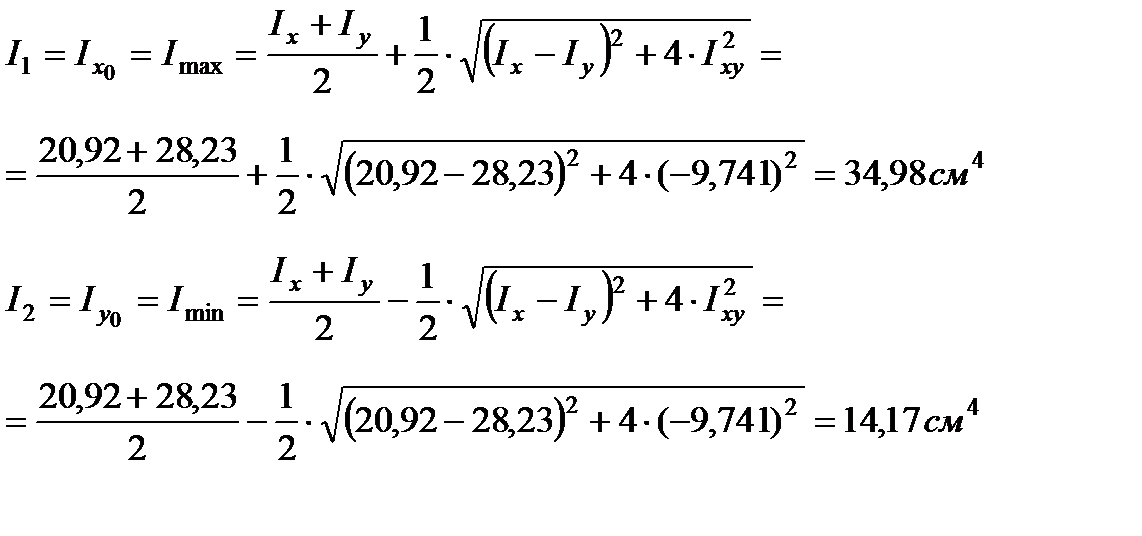
ОПРЕДЕЛЕНИЕ ГЛАВНЫХ МОМЕНТОВ ИНЕРЦИИ ВСЕГО СЕЧЕНИЯ И ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ ГРАФИЧЕСКИМ МЕТОДОМ
Строим точки:
По этим точкам строим окружность диаметра 
(рисунок 4).
При пересечении окружности с осью абсцисс получаем, что:
Через точку D’ x, полученную в результате отображения относительно оси 
точки Dx, проводим ось X0 и определяем угол α0
Рисунок 4 – Круг Мора
Результаты графических вычислений получены с помощью программного обеспечения «Компас».
6 ОПРЕДЕЛЕНИЕ ТОЧЕК СЕЧЕНИЯ НАИБОЛЕЕ УДАЛЕННЫХ ОТ ГЛАВНЫХ ЦЕНТРАЛЬНЫХ ОСЕЙ
Из рисунка 5 видно, что такими точками будут точки 1 и 2, координаты которых в осях X,Y равны:
Координаты точек в осях X0,Y0 равны:
Из полученных результатов следует: 
ОПРЕДЕЛЕНИЕ МОМЕНТОВ СОПРОТИВЛЕНИЯ СЕЧЕНИЯ ИЗГИБУ
ОПРЕДЕЛЕНИЕ РАДИУСОВ ЭЛЛИПСА ИНЕРЦИИ
Радиус 
отложим по оси 
, радиус 
- по оси 
и на этих отрезках построим эллипс инерции (рисунок 5).
Рисунок 5 – Сечение бруса
ЗАКЛЮЧЕНИЕ
Для расчёта на прочность, жёсткость и устойчивость элементов конструкций необходимо знать геометрические характеристики поперечных сечений. В большинстве случаев поперечные сечения брусьев имеют сложную форму. Поэтому нужно уметь определять геометрические характеристики сложных сечений.
В данной работе рассмотрено сложное сечение, составленное из прямоугольника, двутавра и треугольника.
Определены центр тяжести, моменты инерции относительно центральных осей сложного сечения.
Определены главные моменты инерции и положение главных центральных осей аналитическим и графическим методами.
Определены моменты сопротивления сечения изгибу.
Определены главные радиусы инерции и построен эллипс инерции.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Иванов, С.И.. Расчёт на прочность стержневых систем при постоянных и циклически изменяющихся напряжениях [Текст]: задания и метод.указания к расчётно-проектировочным работам [Текст] / С.И. Иванов, В.Ф. Павлов, А.П. Филатов, В.К. Шадрин. – Самара: Изд-во СГАУ. 2010. – 72 с.
2. Шадрин, В.К. Справочные данные к расчётно-проектировочным и курсовым работам по сопротивлению материалов [Текст]: метод.указания [Текст] / В.К. Шадрин, В.С. Вакулюк, В.Б. Иванов [и др.]. – Самара: Изд-во СГАУ. 2007. – 36 с.
3. СТО СГАУ 04068410-004-2007. Общие требования к учебным текстовым документам [Текст]. – Самара: СГАУ. 2007. – 32 с.
.