Задание 1.
Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная.
Тогда ширина интервала составит:
≈ 1,5
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 1 - 2,5 | ||
| 1 - 2,5 | ||
| 1,3 | 1 - 2,5 | |
| 1,3 | 1 - 2,5 | |
| 1,6 | 1 - 2,5 | |
| 1,6 | 1 - 2,5 | |
| 1,8 | 1 - 2,5 | |
| 1,8 | 1 - 2,5 | |
| 1,9 | 1 - 2,5 | |
| 2,1 | 1 - 2,5 | |
| 2,1 | 1 - 2,5 | |
| 2,1 | 1 - 2,5 | |
| 2,2 | 1 - 2,5 | |
| 2,2 | 1 - 2,5 | |
| 2,7 | 2.5 - 4.0 | |
| 2,8 | 2.5 - 4.0 | |
| 2.5 - 4.0 | ||
| 3,8 | 2.5 - 4.0 | |
| 4.0 - 5.5 | ||
| 4,3 | 4.0 - 5.5 | |
| 5,5 | 5.5 - 7.0 | |
| 5,6 | 5.5 - 7.0 | |
| 6,3 | 5.5 - 7.0 | |
| 7,5 | 5.5 - 7.0 | |
| 9,8 | 8.5 - 10.0 |
Аналитическая группировка.
| Группы заводов | Число единиц заводов | Кол-во, nj | X' | Xcp = ∑Xj / nj | ∑Y | Ycp = ∑Yj / nj |
| 1 - 2.5 | 1,2,3,4,5,6,7,8,9,10,11,12,13,14 | 1.75 | 1.71 | 37.6 | 2.69 | |
| 2.5 – 4.0 | 15,16,17,18 | 3.25 | 3.08 | 24.9 | 6.23 | |
| 4.0 - 5.5 | 19,20 | 4.75 | 4.15 | 11.8 | 5.9 | |
| 5.5 – 7.0 | 21,22,23 | 6.25 | 5.8 | 27.7 | 9.23 | |
| 7.0 - 8.5 | 7.75 | 7.5 | 9.6 | 9.6 | ||
| 8.5 – 10.0 | 9.25 | 9.8 | 16.1 | 16.1 | ||
| Итого | 127.7 |
Задание №2(1)
По данным о производительности труда рабочих цеха за смену определить среднюю величину выработки, моду, медиану и показатели вариации выработки (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации)
| Группа рабочих по колличеству продукции выработанной за смену одним рабочим, шт. | Число рабочих с такой выработкой |
| 40-50 | |
| 50-60 | |
| 60-70 | |
| 70-80 | |
| Свыше 80 |
| Группа рабочих по кол-ву продукции выработанной за смену одним рабочим, шт. | Число единиц, f | Центр интервала, x' | х * f | Сумма накопленных частот, S |
|
|
| 40 - 50 | ||||||
| 50 - 60 | ||||||
| 60 - 70 | ||||||
| 70 - 80 | ||||||
| 80 - 90 | ||||||
| Итого |
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная
х = 
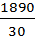= 63;
Мода
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
где 
– начало модального интервала; i – величина интервала; 
–частота, соответствующая модальному интервалу; 
– предмодальная частота; 
– послемодальная частота.
Выбираем в качестве начала интервала 60, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 66,6
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 60 - 70, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 64
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
= Xmax - Xmin
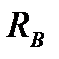= 80 - 40 = 40
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
Каждое значение ряда отличается от другого в среднем на 4.03
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Каждое значение ряда отличается от среднего значения 64.29 в среднем на 7.03
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
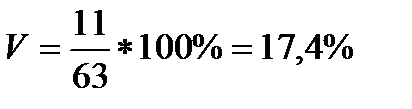
Поскольку v ≤ 33%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Задание №2(2)