Исследование физических моделей
Содержательная постановка задачи. Пушка стреляет в мишень. Необходимо определить угол попадания в мишень. Скорость снаряда 4,5 м/с. Расстояние до площадки 1,5 м, ее длина 14см.
Качественная описательная модель. Из условия задачи можно сформулировать следующие основные предположения:
ü мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
ü ускорение свободного падения можно считать постоянной величиной g=9,8 м/с2 и движение по оси Y можно считать равноускоренным;
ü сопротивлением воздуха можно пренебречь и движение по оси X можно считать равномерным.
Формальная модель. Движение мячика по оси Х равномерное, а по оси Y равноускоренное, поэтому для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания α значения координат дальности полетаx и высоты y от времени можно описать следующими формулами:
X = v0·cosα·t
Y = v0·sinα·t – g·t2/2
Площадка расположена на поверхности земли. Это означает, что конечная координата Y=0. С учетом этого из второй формулы выразим время полета мяча до площадки:
0 = v0·sinα·t – g·t2/2 – вынесем за скобки t
0 = t·(v0·sinα – g·t/2)
Значение времени t = 0 не имеет физического смысла, поэтому:
v0·sinα – g·t/2 = 0 v0·sinα = g·t/2 t = (2·v0·sinα)/g – время полета
Подставим полученное выражение для времени в формулу для вычисления координаты х:
X = (v0·cosα·2·v0·sinα)/g = (v02·sin2α)/g – дальность полета
Формализуем теперь условие попадание мячика в площадку.
Пусть площадка расположена на расстоянии S и имеет длину L. Тогда попадание произойдет, если значение координаты х мячика будет удовлетворять условию в форме неравенства: S≤ х ≤ S+L
Если х<s, то это означает "недолет", а если х>s+l, то это означает "перелет".
Прочесть внимательно.
Первым решением будет построение траектории полета и визуальное определение попадания в мишень. Угол придется подбирать вручную.
Обратите внимание!
Правила формул:
I) Формула начинается со знака равно
II) В формуле используются имена ячеек
III) Имена ячеек пишут на английском языке
(Синус и косинус считают в радианах. Поэтому для перевода градусов используем функцию РАДИАНЫ.)
Ход работы (1 часть Выполняется на 1 листе).
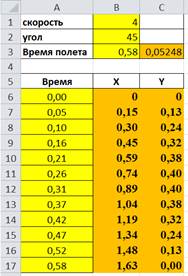
1) Зададим начальную скорость 4 м/с в ячейке B1
2) Запишем в ячейке B2 угол 45 градусов
3) В ячейку B3 введем формулу для вычисления времени полета: =2*B1*SIN(РАДИАНЫ(B2))/9,8
4) В ячейке С3 определим изменение времени для построения траектории по 12 точкам: =B3/11
5) В ячейку A6 введем начало отсчета времени – 0 секунд
6) В ячейку A7 введите формулу для вычисления изменения времени =A6+C$3
7) Используя автозаполнение ячейки до A17
8) В ячейки B6 и C6 введем формулы для вычисления координаты X и Y:
=$B$1*COS(РАДИАНЫ($B$2))*A6
=$B$1*SIN(РАДИАНЫ($B$2))*A6-4,9*A6^2
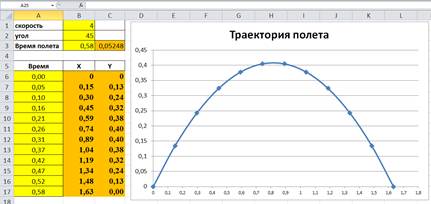
9) 
Построить диаграмму типа Точечная, для которой используется диапазон ячеек B5:С17. (Полученный график это траектория полета)
10) Проанализируйте график. Подберите угол так, чтобы снаряд попадал в мишень. Расстояние до мишени и размер мишени посмотрите в постановке задачи.
Ход работы (2 часть Выполняется на 2 листе).
Исследуем модель и определим угол, который обеспечит попадание в площадку, находящуюся на расстоянии 1.5 м и длиной 14 см, при начальной скорости 4 м/с.
У программы Excel много различных функций, позволяющих легко и просто решить поставленные задачи. Для нашей задачи воспользуемся методом Подбор параметра.
1) Зададим начальную скорость 4 м/с в ячейке B1
2) Запишем в ячейке B2 угол 0 градусов
3) В ячейку B3 введем формулу для вычисления дальности полета:
=B1^2*SIN(РАДИАНЫ(2*B2))/9,8
4) Выделить ячейку В3 и ввести команду в Word 2007 (2010) [ Данные – Анализ «что если» – Подбор параметров ]
5) Заполнить появившееся диалоговое окно «Подбор параметра»
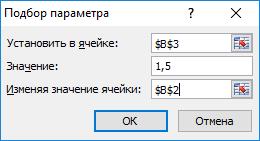
6) Щелкните по кнопке Ок
7) В ячейке В2 будет записано значение угла, при котором будет попадание в переднюю часть мишени.
8) Сохраните файл с результатами работы.