Билинейные и квадратичные формы. Сопряженный и самосопряженный операторы

Теоремы о линейно зависимых и линейно независимых векторах

1. Tеорема 1. Если среди векторов 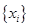есть хоть один нулевой то векторы 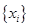линейно зависимы.

2. Tеорема 2. Если к линейно зависимым векторам добавить произвольные векторы , то множество векторов 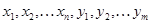будут линейно зависимы.

3. Tеорема 3. Есл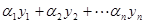и и 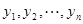линейно независимы, то это представление единственно.

4. Теорема 4. Пусть .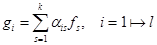

Если векторы линейно независимы, то .

5. Теорема 5. В n -мерном пространстве любую систему линейно независимых векторов 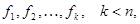можно дополнить до базиса.

6. Теорема 6. Каждый вектор можно представить и притом единственным образом как линейную комбинацию векторов базиса.

 

 

Изоморфизм линейных пространств

 

Теорема 1. Все пространства, имеющие одинаковую размерность, изоморфны друг другу.

Прямая сумма подпространств

1. Теорема 1. Для того чтобы пространство R было разложено в прямую сумму подпространств , необходимо и достаточно, чтобы имели только один общий элемент 0.

2. Теорема 2. Если 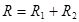-прямая сумма подпространств, то сумма размерностей этих подпространств равна размерности .

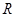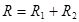3. Теорема 3. Пусть - два подпространства, , . Тогда

dim R +dim R₀ = dim R₁+ dim R₂

 

Формулы преобразования координат

 

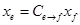, , где

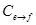–матрица перехода из базиса в базис ; 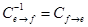– матрица перехода из базиса в базис .

Евклидово пространство

1. Неравенство Коши- Буняковского .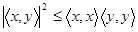

Неравенство Минковского

в евклидовом пространстве R имеет место неравенство

.

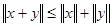3. Теорема 1. Из любого базиса 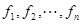можно сделать ортонормированный базис.

4. Теорема 2. Скалярное произведение в ортонормированном базисе равно сумме произведений одноименных координат.

Линейные операторы

1. Теорема 1. Произведение линейных операторов

2. Теорема 2. Матрица произведения операторов равна произведению матриц этих операторов.

3. Теорема 3. Пусть А – произвольный линейный оператор в R. Тогда сумма размерностей образа и ядра равна размерности пространства.

 

Матрица линейного оператора в различных базисах.

 

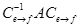
Инвариантные подпространства, собственные векторы и собственные значения линейного оператора.

 

 

1. Теорема 1. Ядро и образ линейного оператора инвариантны.

2. Теорема 2. Характеристический многочлен не зависит от выбора базиса.

3. Теорема 3. Если оператор А имеет различные собственные значения , то соответствующие им собственные векторы линейно независимы

Билинейные и квадратичные формы. Сопряженный и самосопряженный операторы

1. Теорема 1. В евклидовом пространстве существует взаимно однозначное соответствие между линейными операторами и билинейными формами.

2. Теорема 2. Образ оператора и ядро сопряженного оператора ортогональны.

3. Теорема 3. Собственные числа самосопряженного оператора вещественны.

4. Теорема 4. Пусть 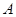– самосопряженный оператор. Тогда у оператора существуют n попарно ортогональных собственных векторов.

5. Теорема 5. Пусть 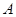– самосопряженный оператор. Тогда существует ортогональный базис, в котором матрица преобразования диагональна и вещественна.

6. Теорема 6. Собственные векторы, отвечающие различным собственным числам ортогональны.

7. Теорема 7. Образ самосопряженного оператора и его ядро ортогональны.

8. Теорема 8. Пусть 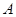- линейный самосопряженный оператор в евклидовом пространстве 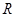над полем вещественных чисел и пусть 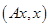– его квадратичная форма. Тогда в 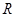существует ортонормированный базис, в котором квадратичная форма равна сумме квадратов: .

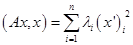9. Теорема 9. Число отрицательных коэффициентов в квадратичной форме, приведенной к сумме квадратов, равно числу перемен знака в последовательности определителей .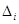

10. Теорема Сильвестра. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все .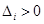

11. Закон инерции. Если квадратичная форма приведена к сумме квадратов, то число положительных и отрицательных коэффициентов, а следовательно, и нулевых будет одно и то же.