ГЛАВА 5. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Правило Лопиталя
Наряду с основным приемом нахождения пределов функции - методом выделения главной части, существуют и другие способы отыскания пределов. Здесь будут представлены три теоремы, с помощью которых можно находить пределы типа  .
.
Теорема 1. Пусть функции  и
и 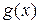 удовлетворяют условиям:
удовлетворяют условиям:
а) определены и дифференцируемы в некоторой окрестности точки  за исключением может быть самой точки
за исключением может быть самой точки  ;
;
б) пусть также  ;
;
в) 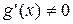 в проколотой окрестности точки
в проколотой окрестности точки  ;
;
г) существует  ,
,
тогда существует  , причем
, причем 
□ По условию  и
и  . Доопределим
. Доопределим  и
и 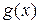 в точке
в точке  , а именно положим
, а именно положим  . Так как
. Так как  и
и 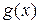 дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 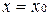 , то они непрерывны в этой окрестности точки
, то они непрерывны в этой окрестности точки  , то есть на отрезке
, то есть на отрезке  . По условию,
. По условию, 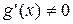 откуда следует, что
откуда следует, что  при
при  . Тогда можно записать формулу Коши на сегменте
. Тогда можно записать формулу Коши на сегменте  .
.


 .
.
Если  , то
, то  +0, следовательно
+0, следовательно

 . Аналогично, если
. Аналогично, если 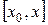 и
и 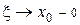 . ■
. ■
Теорема 2. Пусть функции  и
и 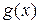 удовлетворяют условиям:
удовлетворяют условиям:
а) определены и дифференцируемы при  :
:
б)  :
:
в)  :
:
г) существует предел  ,
,
Тогда существует и предел  , причем они равны, т.е.
, причем они равны, т.е.

□ Без ограничения общности можно считать, что  . Сделаем замену
. Сделаем замену  . Тогда, очевидно, что функции
. Тогда, очевидно, что функции  и
и  определены в интервале
определены в интервале  и
и  .
.
 ,
,  .
.
Тогда в силу теоремы 1, имеем: 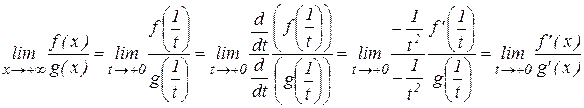 .
.
Теорема справедлива, и если  . ■
. ■
Теорема 3. Пусть функции  и
и 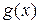 :
:
а) определены и дифференцируемы в окрестности точки  , за исключением может быть самой точки
, за исключением может быть самой точки  ;
;
б)  ;
;
в) 
 ;
;
г) существует предел 
 .
.
Тогда существует предел  , причем
, причем
 .
.
Замечание 1. В силу теорем 1-3 существует общий способ нахождения предела отношения двух функций, основанный на равенстве  . Этот способ называется правилом Лопиталя.
. Этот способ называется правилом Лопиталя.
Замечание 2. Если для производных 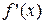 и
и  выполняют условия теорем 1-3, то правило Лопиталя можно применить повторно, т.е.
выполняют условия теорем 1-3, то правило Лопиталя можно применить повторно, т.е. 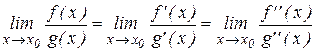 .
.
Пример 1. Вычислить пределы с помощью правила Лопиталя:
1)  . 2)
. 2)  . 3)
. 3) 
 .
.
Кроме неопределенностей 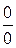 и
и  встречаются еще неопределенности других типов.
встречаются еще неопределенности других типов.
Под раскрытием неопределенности типа 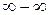 понимают нахождение предела
понимают нахождение предела  , когда
, когда  и
и  .
.
Под неопределенностью типа  понимают нахождение предела
понимают нахождение предела  , если
, если 
 и
и  .
.
Есть и другие неопределенности:  ;
;  ;
; 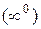 .
.
Неопределенности типа 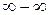 и
и  сводятся к неопределенностям
сводятся к неопределенностям 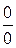 или
или  путем алгебраических преобразований.
путем алгебраических преобразований.
Другие неопределенности обычно сводятся к неопределенностям 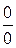 или
или  путем логарифмирования выражения
путем логарифмирования выражения 
Пример 2. Вычислить пределы с помощью правила Лопиталя:
1)  ;2)
;2) 
 ; 3)
; 3)  ;
;
4)  .
.
Формула Тейлора
Здесь будет доказана формула, которая является одной из основных в математическом анализе и имеет многочисленные приложения, как в самом анализе, так и в других дисциплинах.
Теорема 4. ( Тейлор ). Пусть функция  имеет в некоторой окрестности т.
имеет в некоторой окрестности т.  (n+1)- ю производную, x – любое значение аргумента из этой окрестности и p – произвольное положительное число. Тогда между точками
(n+1)- ю производную, x – любое значение аргумента из этой окрестности и p – произвольное положительное число. Тогда между точками  и
и  найдется также точка
найдется также точка 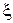 , что будет справедлива формула Тейлора.
, что будет справедлива формула Тейлора.
 , (1)
, (1)
где  . (2)
. (2)
Выражение  называется остаточным членом в формуле Тейлора, записанным в общей форме или в форме Шлемильха-Роша.
называется остаточным членом в формуле Тейлора, записанным в общей форме или в форме Шлемильха-Роша.
□ Обозначим  многочлен, стоящий в (1), т.е.
многочлен, стоящий в (1), т.е.
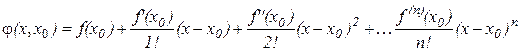
Тогда формула (1) имеет вид

или
 ( 3 )
( 3 )
 Формула Тейлора (1) будет доказана, если будет установлено, что
Формула Тейлора (1) будет доказана, если будет установлено, что  определяется по формуле (2).
определяется по формуле (2).
Возьмем в окрестности точки 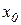 некоторое число
некоторое число 
и рассмотрим отрезок  . Рассмотрим вспомогательную функцию переменной t
. Рассмотрим вспомогательную функцию переменной t  , которую получим из (3):
, которую получим из (3):
 (4)
(4)
Эта функция удовлетворяет условиям т. Ролля по переменной t. Она непрерывна и дифференцируема на  , т.к.
, т.к.  дифференцируема
дифференцируема  раз. Вычислим значения на концах отрезка
раз. Вычислим значения на концах отрезка  .
.
Запишем  подробнее:
подробнее:

 на
на  .
.
 , т.е.
, т.е. 
При  имеем
имеем

 из формулы (3) по определению
из формулы (3) по определению  . Т.е.
. Т.е.  . Тогда по теореме Ролля
. Тогда по теореме Ролля  , что
, что  . Найдем
. Найдем 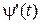 :
:

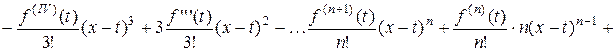
 .
.
Таким образом  .
.


 .
.

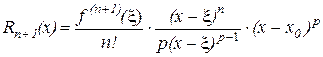 .
.
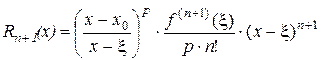 .
.
Таким образом доказано, что остаточный член имеет вид (2), если имеет место формула (1). ■
Замечание 1. Ясно, что аналогичное доказательство будет, если  , т.е. если брать точку
, т.е. если брать точку  слева от точки
слева от точки  .
.
Замечание 2. Если 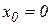 , то формула Тейлора называется формулой Маклорена и имеет вид:
, то формула Тейлора называется формулой Маклорена и имеет вид:
 . (5)
. (5)
Замечание 3. Рассмотрим частный случай, разложение по формуле Тейлора алгебраического многочлена, т.е.
 .
.
Так как  , то
, то  , и формула принимает вид:
, и формула принимает вид:
 .
. 
Здесь  - любая точка вещественной прямой. Таким образом, любой многочлен можно представить как многочлен по степени
- любая точка вещественной прямой. Таким образом, любой многочлен можно представить как многочлен по степени  , где
, где  - любое число.
- любое число.
Замечание 4. Обозначим  ,
,  .
.
Тогда  :
:  и формула Тейлора в дифференциальной форме будет иметь вид:
и формула Тейлора в дифференциальной форме будет иметь вид:

или
 .
.
Формула Тейлора выведена с остаточным членом в общей форме. Существуют и другие виды остаточного члена.
 Обозначим
Обозначим  ,
,  .
.
1) Положим  . Тогда
. Тогда
 .
.
или
 .
.
Такой вид остаточного члена называется остаточным членом в форме Лагранжа.
2) Положим  . Тогда
. Тогда
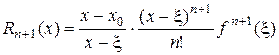 ,
,  .
.
 .
.
или
 - остаточный член в форме Коши.
- остаточный член в форме Коши.
3) Пусть функция  непрерывна в точке
непрерывна в точке  , следовательно функция
, следовательно функция  также непрерывна в точке
также непрерывна в точке  , т.к.
, т.к. 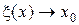 при
при  , т.е.
, т.е.  при
при  . Запишем формулу Тейлора с остаточным членом
. Запишем формулу Тейлора с остаточным членом  и затем преобразуем её:
и затем преобразуем её:
 .
.
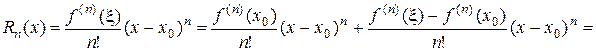
 .
. 

 т.к.
т.к.  при
при  .
.
Таким образом 
 .
.
Последнее слагаемое

называется остаточным членом в формуле Пеано. Итак
 .
.
Очевидно, что разные формы остаточного члена верны и при  , т.е. при
, т.е. при  .
.
Представления основных элементарных функций с помощью формулы Тейлора.
Практическая значимость формулы Тейлора состоит в том, что она позволяет заменить функцию  , имеющую на промежутке
, имеющую на промежутке  производные до
производные до  -го порядка включительно, многочленом
-го порядка включительно, многочленом  -й степени
-й степени
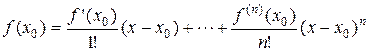 ,
,
а различные формы остаточного члена позволяют оценить возникающую при этом погрешность. Таким образом формула Тейлора может быть использована для получения различных формул для приближенного вычисления значений функций.
Пусть  обладает следующими свойствами:
обладает следующими свойствами:  , что
, что  и
и  из окрестности точки
из окрестности точки  выполняются условия:
выполняются условия:  , т.е. все производные равномерно ограничены.
, т.е. все производные равномерно ограничены.
Возьмем остаточный член в формуле Лагранжа при  .
.
 , т.к
, т.к  ,
,
то получим:
 .
.
Это есть универсальная оценка остаточного члена.
Поскольку  , то выбирая достаточно большой номер
, то выбирая достаточно большой номер  можно сделать остаточный член как угодно малым.
можно сделать остаточный член как угодно малым.
Получим представление некоторых элементарных функций с помощью формулы Тейлора по степеням  , т.е. по формуле Маклорена, когда
, т.е. по формуле Маклорена, когда  .
.
1.  .
.
 .
.
Тогда формула Маклорена для функции  будет иметь вид:
будет иметь вид:
 .
.
Остаточный член в форме Лагранжа ( ):
):
 ;
; 
При любом фиксированном  , остаток стремится к 0, т.к.
, остаток стремится к 0, т.к.
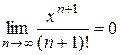 .
.
2.  ;
; 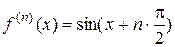 ;
;  .
.
При  .
.
При  и
и
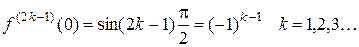
Если  , то
, то  .
.
Разложение функции  по формуле Маклорена будет иметь вид:
по формуле Маклорена будет иметь вид:
 .
.
3.  ;
;  ;
;
При 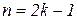
 .
.
При 
 .
.
 .
.
Разложение функции  по формуле Маклорена будет иметь вид:
по формуле Маклорена будет иметь вид:
 .
.
Остаточный член  при
при  .
.
4.  ;
;
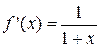 ;
;  ;
;  :
: 
 .
.

Разложение функции  по формуле Маклорена будет иметь вид:
по формуле Маклорена будет иметь вид:
 .
.
Остаточный член в форме Лагранжа
 ;
;
 , т.е.
, т.е.  при
при  .
.
5.  ;
;  .
.
Разложение функции  по формуле Маклорена будет иметь вид:
по формуле Маклорена будет иметь вид:
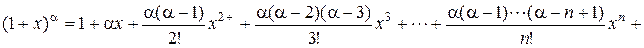
 .
.
 .
. 
При 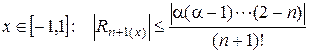
Ясно, что при  - целое число, то получим бином Ньютона
- целое число, то получим бином Ньютона
 .
.
Пусть функция  имеет в окрестности точки
имеет в окрестности точки  все производные до n-го порядка включительно. Запишем формулу Тейлора с остаточным членом в ряде Пеано.
все производные до n-го порядка включительно. Запишем формулу Тейлора с остаточным членом в ряде Пеано.

 .
.
Этой формулой удобно пользоваться для вычисления пределов.
Пример 3. Вычислить пределы, разложив функцию по формуле Тейлора.
1) 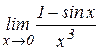 .
.
При  имеем
имеем  , тогда
, тогда
 .
.
Здесь использовано:  .
.
2)  .
.
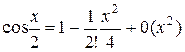 ;
;  ;
; 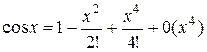
3) 
 .
.
Исследование функций
Монотонность. Теорема 5. ( Необходимый и достаточный признак монотонности). Для того чтобы дифференцируемая на открытом промежутке  функция
функция  не убывала (не возрастала) на этом промежутке необходимо и достаточно, чтобы:
не убывала (не возрастала) на этом промежутке необходимо и достаточно, чтобы:
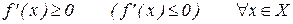 .
.
□  Необходимость. Пусть
Необходимость. Пусть  дифференцируема и не убывает на
дифференцируема и не убывает на  . Докажем, что
. Докажем, что  .
.
Рассмотрим отношение 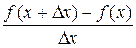 .
.
Если  , то
, то 
 .
.
Перейдем к пределу при  , и по теореме сравнения получим
, и по теореме сравнения получим
 .
.
Аналогично доказывается в случае не возрастания функции.
Достаточность. Пусть 
 . Докажем, что
. Докажем, что  не убывает.
не убывает.
Пусть 
 , причем
, причем  . На отрезке
. На отрезке 
 непрерывная и дифференцируемая, следовательно выполняется теорема Лагранжа:
непрерывная и дифференцируемая, следовательно выполняется теорема Лагранжа:
 . (6)
. (6)

и  не убывает. ■
не убывает. ■
Следствие. Если  , то
, то  строго возрастает на
строго возрастает на  , если
, если  , то
, то  строго убывает на
строго убывает на  .
.
Справедливость следует из (6).
Отметим, что условия  и
и  не являются необходимыми для строгого возрастания и убывания. Например,
не являются необходимыми для строгого возрастания и убывания. Например, 
 , а функция
, а функция  строго возрастает всюду.
строго возрастает всюду.
Теорема остается справедливой для непрерывных функций, не имеющих производных в конечном числе точек. Для проверки достаточно ее последовательно применить ко всем промежуткам, на которые разбивается заданный интервал множеством точек, где производные не существуют.
Экстремумы. Пусть  определена на открытом промежутке
определена на открытом промежутке  .
.
Определение 1. Точка 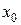 называется точкой максимума функции
называется точкой максимума функции  , если существует некоторая окрестность точки
, если существует некоторая окрестность точки  , что
, что
 .
.
Точка  называется точкой минимума функции
называется точкой минимума функции  , если
, если
 .
.
Если выполняется условие  (или
(или  ), то
), то  называется точкой строгого максимума (строгого минимума).
называется точкой строгого максимума (строгого минимума).
очки максимума и минимума (строгого max и строгого min) называются точками экстремума функции  .
.
Очевидно, что если  , то
, то  точка максимума. Если
точка максимума. Если  , то
, то  точка минимума.
точка минимума.

Теорема 6. (Ферма, необходимый признак экстремума ). Если дифференцируемая в окрестности точки  и функция
и функция  имеет в точке
имеет в точке  экстремум, то
экстремум, то 
□ Пусть при  имеется экстремум, например максимум. Тогда
имеется экстремум, например максимум. Тогда  и
и  . Откуда
. Откуда


Так как функция дифференцируемая, то предел в определении производной
 не зависит от того, как стремится
не зависит от того, как стремится  слева или справа. Но если
слева или справа. Но если  , то
, то  , а если
, а если  , то
, то  . Следовательно
. Следовательно  .
.
Аналогичное доказательство и для минимума. ■
 есть экстремум, то касательная к кривой в этой точке параллельна OX.
есть экстремум, то касательная к кривой в этой точке параллельна OX.
|

|
Точки, в которых  называются стационарными. Точки, в которых первая производная равна 0 или не существуют, называются критическими.
называются стационарными. Точки, в которых первая производная равна 0 или не существуют, называются критическими.
Теорема 7. ( I-й достаточный признак экстремума ) Пусть функция  непрерывна в некоторой окрестности критической точки
непрерывна в некоторой окрестности критической точки  и дифференцируема в этой окрестности (за исключением, может быть самой точки
и дифференцируема в этой окрестности (за исключением, может быть самой точки  ). Тогда, если при
). Тогда, если при  , а при
, а при  , то
, то  - точка строго локального максимума. Если при
- точка строго локального максимума. Если при 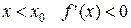 , а при
, а при  , то
, то  - точка строгого минимума.
- точка строгого минимума.
□ Пусть знак 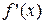 меняется с + на – в точке
меняется с + на – в точке  .
.
|

 при
при  .
.

 при
при  .
.
На отрезке  запишем формулу Лагранжа:
запишем формулу Лагранжа:
 .
.
На  формула Лагранжа имеет вид:
формула Лагранжа имеет вид:
 .
.
Таким образом  , следовательно
, следовательно  - точка строгого max. Для min доказательство аналогично. ■
- точка строгого max. Для min доказательство аналогично. ■
Пример 4. Определить интервалы монотонности и найти экстремумы.
1)  . Найдем сначала критические точки.
. Найдем сначала критические точки.
 .
. 
Проверим признак в каждой критической точке, одновременно исследуя монотонность.

 |

 | |||
|
2)  поэтому экстремумов нет и функция всюду возрастает.
поэтому экстремумов нет и функция всюду возрастает.
3)  ;
;  . Производная в точке
. Производная в точке  не существует, но при переходе через неё изменяет знак с плюса на минус, поэтому
не существует, но при переходе через неё изменяет знак с плюса на минус, поэтому  есть точка max.
есть точка max.
4)  ;
; 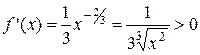 . Функция всюду возрастает, экстремумов нет.
. Функция всюду возрастает, экстремумов нет.
Теорема 8. (II-й достаточный признак экстремума). Пусть  дважды непрерывно дифференцируема в окрестности точки
дважды непрерывно дифференцируема в окрестности точки  и
и  . Тогда, если
. Тогда, если  , то
, то  - точка максимума, если
- точка максимума, если  , то
, то  - точка минимума.
- точка минимума.
□ Разложим  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  по степеням
по степеням 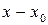 при
при 
 , (7)
, (7)
где
 .
.
Поскольку  , то из (7), получаем:
, то из (7), получаем:


Пусть  т.к.
т.к.  непрерывна в окрестности точки
непрерывна в окрестности точки  ,
,
то 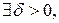 что
что 
 т.е.
т.е.  .
.

|
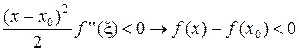 и
и
 . Т.е
. Т.е  –точка максимума.
–точка максимума.
Аналогично теорема доказывается в случае минимума. ■
Пример 5. Найти экстремумы функции  при
при  .
.
 .Производная равна нулю в точках
.Производная равна нулю в точках  и
и  .
.
Находим вторую производную и вычисляем её в этих точках:

В точке  -минимум, а в точке
-минимум, а в точке  -максимум.
-максимум.
Теорема 9. Пусть  непрерывна и дифференцируема
непрерывна и дифференцируема  раз в окрестности точки
раз в окрестности точки  , причем
, причем 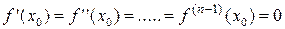 , но
, но  , тогда:
, тогда:
а) если  -четное и
-четное и  , то
, то  точка максимума.
точка максимума.
б) если  -четное и
-четное и  , то
, то  точка минимума.
точка минимума.
в) если  - нечетное, то
- нечетное, то  в точке
в точке  не имеет экстремума.
не имеет экстремума.
Доказать самостоятельно, записав формулу Тейлора для  членов.
членов.
Замечание 1. Если  не существует, то исследование на
не существует, то исследование на  проводят с помощью 1-ого признака.
проводят с помощью 1-ого признака.
Замечание 2. По теореме Вейерштрасса, функция непрерывная на отрезке  принимает на нем свое max и min значения (достигает
принимает на нем свое max и min значения (достигает  и
и  ). Тогда наибольшее и наименьшее значения функция
). Тогда наибольшее и наименьшее значения функция  на
на  принимает либо на концах отрезка в точках
принимает либо на концах отрезка в точках  и
и 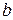 ,либо в точке локального max и min.
,либо в точке локального max и min.
Выпуклость и точки перегиба функции. Пусть функция  дифференцируема в окрестности точки
дифференцируема в окрестности точки  .Тогда уравнение
.Тогда уравнение
 (
( )
)
есть уравнение касательной к графику  в точке
в точке  .
.
Определение 3. Функция  называется выпуклой (выпуклой вверх) в окрестности точки
называется выпуклой (выпуклой вверх) в окрестности точки  , если выполняется условие:
, если выполняется условие:
 ,
,
т.е. график  расположен ниже касательной в точке
расположен ниже касательной в точке  (рис.4а).
(рис.4а).
Фу

