Практическая работа № 2.
Информационная емкость сигналов существенно зависит от типа сигналов и определяет требования к каналам передачи данных (каналам связи), равно как и технические характеристики каналов связи определяют требования к информационной емкости сигналов, передаваемых по этим каналам.
Для каналов передачи дискретных сигналов (дискретные канала связи) используют понятия технической и информационной скорости передачи данных.
Под технической скоростью передачи подразумевают число элементарных сигналов (символов), передаваемых по каналу в единицу времени. Простейший элементарный символ – однополярный электрический импульс длительностью t на тактовом интервале T. В дискретных каналах используют, как правило, двуполярные импульсы, положительные на первой половине интервала Т и отрицательные на второй половине. Это позволяет поддерживать нулевой потенциал кабеля и выполнять тактовую синхронизацию приемо-передачи сигналов.
Единицей измерения технической скорости Vt = 1/T служит БОД – один символ в секунду.
Полоса пропускания канала связи обычно ограничивается определенной предельной частотой Fпред по уровню затухания сигнала до уровня статистических помех, при этом значение технической скорости передачи данных, естественно, не может быть выше Fпред без каких-либо специальных устройств выделения информационных сигналов.
При известной технической скорости VT скорость передачи информации измеряется в битах в секунду, и при уровне помех меньше амплитудных значений символьных импульсов задается соотношением:
Vh = Vt H(s),
где H(s) – энтропия символа.
Для двоичных дискретных символов с возможными состояниями [0, 1] (однополярные – есть/нет импульс на такте, для двуполярных – порядок полярности импульсов на такте, например, 0: плюс/минус, 1: минус/плюс) при постоянной амплитуде импульсов значение H(s) равно 1. При числе L возможных равновероятных уровней амплитуды импульсов (уровень помех меньше разности уровней амплитуд импульсов) значение H(s) равно log L.
Информационная емкость сигнала или полное количество информации в сигнале S (сообщении, кодовой последовательности/слове) определяется полным количеством N = t/T энтропии символов в битах на интервале задания сигнала t:
It(S) = N log L = (t/T) log L.
Увеличение числа уровней L увеличивает пропускную способность каналов связи, но усложняет аппаратуру кодирования данных и снижает помехоустойчивость связи.
Для непрерывных сигналов передача по каналам связи возможна только при условии, что максимальная информационная частота в сигнале Fmax не превышает предельной частоты Fпред передачи сигналов каналом связи. Для оценки информационной емкости непрерывного сигнала выполним его дискретизацию с интервалом Dt = 1/2Fmax.
Как установлено Котельниковым в 1933 году, по мгновенным отсчетам непрерывного сигнала с таким интервалом дискретизации аналоговый сигнал может быть восстановлен без потери информации. При полной длительности сигнала Ts число отсчетов:
N = Ts/Dt = 2Fmax Ts.
Определим максимально возможное число выборок в каждом отсчете при наличии шума в канале со средней мощностью Рш = d2. При средней мощности сигнала Ps = s2:
L =  =
=  .
.
Информационная емкость сигнала:
I(S) = 2Fmax Ts log L.
Информационные возможности сигнала возрастают с расширением его спектра и превышением его уровня над уровнем помех.
Пример 1. Источник вырабатывает 3 сообщения с вероятностями:
p1 = 0,1; p2 = 0,2 и p3 = 0,7.
Сообщения независимы и передаются равномерным двоичным кодом (m = 2) с длительностью символов, равной 1 мс. Определить скорость передачи информации по каналу связи без помех.
Решение: Энтропия источника равна

 [бит/с].
[бит/с].
Для передачи 3 сообщений равномерным кодом необходимо два разряда, при этом длительность кодовой комбинации равна 2t.
Средняя скорость передачи сигнала
V =1/2 t = 500 [1/c].
Скорость передачи информации
C = vH = 500×1,16 = 580 [бит/с].
Пример.2 По каналу связи передаются сообщения, вероятности которых соответственно равны:
p(x1)=0,1; p(x2)=0,2; p(x3)=0,3; p(x4)=0,4.
Канальная матрица, определяющая потери информации в канале связи имеет вид:

|
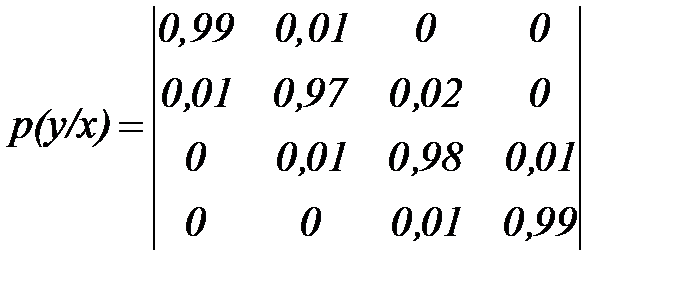 .
.
Определить:
1. Энтропию источника информации – H(X).
2. Безусловную энтропию приемника информации – H(Y).
3. Общую условную энтропию – H (Y/X).
4. Скорость передачи информации, если время передачи одного символа первичного алфавита t = 0,1 мс.
5. Определить потери информации в канале связи при передаче 500 символов алфавита.
6. Среднее количество принятой информации.
7. Пропускную способность канала связи.
Решение:
1. Энтропия источника сообщений равна

2. Вероятности появления символов на входе приемника


Проверка:

Энтропия приемника информации равна
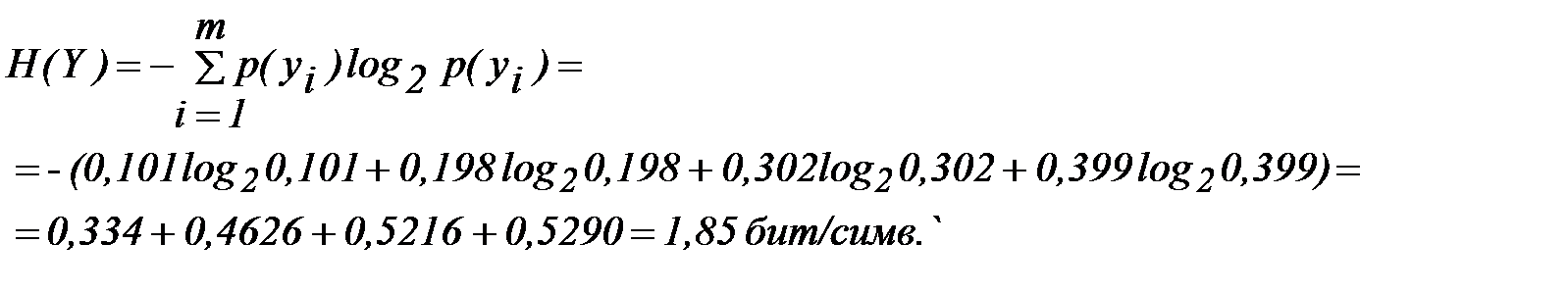
3. Общая условная энтропия равна

4. Скорость передачи информации равна:
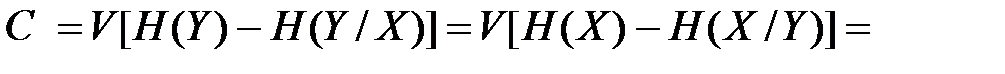
=(1,85–0,132)/0,0001=17,18 Кбит/с. 
5. Потери информации в канале связи при передаче 500 символов алфавита равны:
 500×0,132=66 бит.
500×0,132=66 бит.
6. Среднее количество принятой информации равно:

=500×(1,85–0,132)=859 бит.
7. Пропускная способность канала связи
 (2–0,132)/0,0001=18,68 Кбит/с.
(2–0,132)/0,0001=18,68 Кбит/с.