Упражнение 1. Найти указанные пределы.
Решение:
1) 
2) 
При подстановке вместо переменно х ее предельного значения 3 получается неопределенность вида 
. Для избавления от этого типа неопределенности в этом случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой 
, где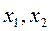 
- корни квадратного трехчлена 
. У нас 
, т.к. дискриминант квадратного трехчлена 
, а следовательно, 
.
Аналогично 
.
Теперь условие примера можно переписать а другом виде и продолжить решение:
.
3) 
.
Здесь сталкиваемся с неопределенностью вида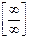 
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной: 
.
4) 
.
В данном случае для освобождения от возникшей неопределенности вида будем использовать I замечательный предел и одно из его очевидных следствий:
.
Решение примера будет выглядеть следующим образом:
Упражнение 2. Найти производные, пользуясь правилами и формулами дифференцирования.
Решение:
Кроме формул дифференцирования нужно использовать правила дифференцирования (суммы, разности, произведения, частного).
Необходима и теорема о производной сложной функции:
если задана сложная функция 
, где 
, то есть 
; если каждая из функций и дифференцируема по своему аргументу, то
.
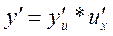1) 
, 
,
.
2) 
,
3) 
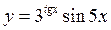
4) 
Упражнение 3. Исследовать функцию методами дифференциального исчисления и начертить график.
Исследование функции и построение графика рекомендуется проводить по следующей схеме:
1) найти область определения функции D(y);
2) найти точки экстремума функции и определить интервалы ее монотонности;
3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;
4) найти асимптоты графика функции;
5) построить график, используя результаты предыдущих исследований;
6) дополнительно найти наибольшее и наименьшее значения на отрезке 
.
Решение:
Дана функция: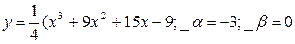 
1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y): 
, а это значит, что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
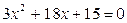
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки I рода х1 = -5, х2 = -1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
| x | 
| -5 | 
| -1 | 
|
| + | - | + | ||
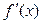
| & | max | ( | min | & |
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем II производную заданной функции и приравняем ее к нулю:
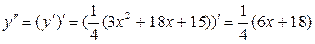
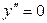, т.е. 
Итак, функция имеет одну критическую точку 2 рода . Разобьем область определения полученной точкой на части, в каждой из которой установим знак II производной:
| x | 
| -3 |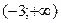 
|
| - | + | |
|
| 
| т.п. | 
|
Значение является абсциссой точки перегиба графика функции, а ордината этой точки 
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты 
воспользуемся формулами: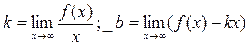 
.
Имеем 
.
Таким образом, у графика заданной функции наклонных асимптот нет.
5) 
Для построения графика в выбранной системе координат изобразим точки максимума А1(-5; 4), минимума А2(-1; -4), перегиба А3 (-3; 0) и точку пересечения графика с осью Оу А4 (0; 
). С учетом результатов предыдущих исследований построим кривую.
6) Найдем наибольшее и наименьшее значения заданной функции на отрезке 
. Для этого посчитаем значения функции на концах этого отрезка, в критических точках I рода, попавших на отрезок, и сравним результаты:
.
Очевидно, что 
.
Упражнение 4. Задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t0.
Решение:
Пусть 
.
Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент I и II производных функции, задающей закон изменения пути движения точки.
У нас 
(ед. ск.)
(ед. уск.)
Упражнение 5. Найти неопределенные интегралы
а) способом подстановки (методом замена переменной) 
, 
;
б) применяя метод интегрирования по частям 
, 
.
Решение:
а) : применим подстановку 
. Тогда 
и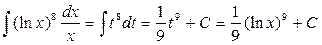 
: применим подстановку 
. Тогда 
,
, откуда 
б) : применим формулу интегрирования по частям 
.
Положим 
. Тогда 
.
Следовательно, 
.
: положим 
. Тогда 
.
Отсюда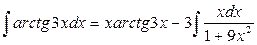 
. Применяя в последнем интеграле подстановку 
, получаем 
, следовательно, 
.
Отсюда 
.
Упражнение 6. В ычислить площадь плоской фигуры, ограниченную параболами.
Решение:
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений: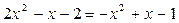 
.
Решаем полученное квадратное уравнение: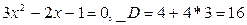 
.
Вычисление площади фигуры осуществляем по формуле 
, где 
- кривые, ограничивающие фигуру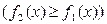 
.
В нашем случае 
(кв. ед.)
Упражнение 7. Дискретная случайная величина Х имеет только два возможных значения х1 и х2, причем х1 < х2. Найти закон распределения величины Х, если известно, что математическое ожидание М (х) = 1,4, дисперсия D (х) = 0,24 и вероятность р1 того, что Х примет значение х1, равна 0,6.
Решение:
Так как сумма вероятностей всех возможных значений Х равна 1, то вероятность p2 того, что Х примет значение х2, равна p2 = 1 - p1 = 1 – 0,6 = 0,4.
Напишем закон распределения Х:
| Х | х1 | х2 |
| p | 0,6 | 0,4 |
Для отыскания х1 и х2 составим два уравнения.
Для составления первого уравнения воспользуемся тем, что математическое ожидание
M(x) определяется по формуле M(x) = х1 р1 + х2 р2 + … + хn рn
В нашем случае: M(x) = х1 р1 + х2 р2
Учитывая, что по условию M(x) = 1,4, можем записать первое уравнение:
0,6х1 + 0,4х2 = 1,4.
Учитывая, что по условию D(x) = 0,24, пользуясь формулой D (х) = M (X2) – [M(X)]2, напишем второе уравнение:
0,6 х12 + 0,4 х22 - 1,42 = 0,24, или
0,6 х12 + 0,4 х22 = 2,2.
Решив полученную систему уравнений, найдем два решения:
х1 = 1, х2 = 2 и х1 = 1,8, х2 = 0,8.
По условию, х1 < х2, поэтому задаче удовлетворяет лишь первое решение.
Окончательно получим искомый закон распределения:
| Х | ||
| p | 0,6 | 0,4 |
Упражнение 8. Найти решение системы линейных уравнений:
а) методом Крамера
б) методом Гаусса
Решение:
Метод Крамера
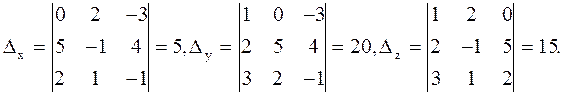
Проверка:
Ответ: x=0,5; y=2; z=1,5.
Метод Гаусса
x1 – 2x2 + x3 + x4 = –1;
3x1 + 2x2 – 3x3 – 4x4 = 2;
2x1 – x2 + 2x3 – 3x4 = 9;
x1 + 3x2 – 3x3 – x4 = –1.
Решение:Составим матрицу В и преобразуем ее. Для удобства вычислений отделимвертикальной чертой столбец, состоящий из свободных членов:
1 –2 1 1 –1
B = 3 2 –3 –4 2
2 –1 2 –3 9
1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу,эквивалентную исходной:
1 –2 1 1 –1
0 8 –6 –7 5
0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
|
1 –2 1 1 –1
0 –1 –6 8 –28
0 0 –1 0 –3
0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
x1 – 2x2 + x3 + x4 = –1;
– X2 – 6x3 + 8x4 = –28;
– x3 = –3;
19x4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x4 = –1, из третьего х3 = 3. Подставив значения х3 и x4 во второе уравнение, найдем x2 = 2. Подставив значения x2, x3, x4 в первое уравнение, найдем x1 = 1.
Ответ. (1; 2; 3;-1).
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ
В задачах 1-10 найти указанные пределы:
№ 1.
1) 
; а) х0 = 2; б) х0 = - 1; в) х0 = ¥ 2). 
№ 2.
1) 
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥ 2). 
№ 3.
1) 
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥ 2). 
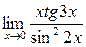
№ 4.
1) 
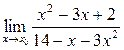; а) х0 = 1; б) х0 = 2; в) х0 = ¥ 2). 
№ 5.
1) 
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥ 2). 
№ 6.
1) 
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥ 2). 
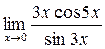
№ 7.
1) 
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥ 2). 
№ 8.
1) 
; а) х0 = 1; б) х0 = 2; в) х0 = ¥ 2). 
№ 9.
1) 
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥ 2). 
№ 10.
1) 
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥ 2). 
В задачах 11-20 найти производные, пользуясь правилами и формулами дифференцирования:
№ 11.
а). 
б). 
в). 
г). 
№ 12.
а). 
б). 
в). 
г). 
№ 13.
а). 
б). 
в).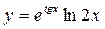 
г). 
№ 14.
а). 
б). 
в). 
г). 
№ 15.
а). 
б). 
в). 
г). 
№ 16.
а). 
б). 
в). 
г). 
№ 17.
а).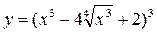 
б). 
в). 
г). 
№ 18.
а).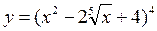 
б).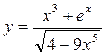 
в). 
г). 
№ 19.
а). 
б). 
в). 
г). 
№ 20.
а). 
б).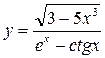 
в). 
г). 
В задачах 21-30 исследовать функцию методами дифференциального исчисления и начертить график:
№ 21
№ 22
№ 23
№ 24
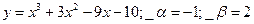
№ 25
№ 26
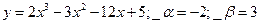
№ 27
№ 28
№ 29
№ 30
В задачах 31-40 задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t0:
№ 31
№ 32
№ 33
№ 34
№ 35
№36
№ 37
№ 38
№ 39
№ 40
