НОУ ВПО ИНСТИТУТ ЗАКОНОВЕДЕНИЯ И УПРАВЛЕНИЯ
ВСЕРОССИЙСКОЙ ПОЛИЦЕЙСКОЙ АССОЦИАЦИИ
КАФЕДРА ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН И
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Контрольные задания и методические рекомендации
Для выполнения контрольной работы
по дисциплине «Математика»
для студентов заочной формы обучения
(1 курс, 2 семестр)
Тула 2015
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Настоящее пособие предназначено для студентов заочного отделения института законоведения и управления всероссийской полицейской ассоциации. Контрольно-курсовая работа (далее ККР) охватывают следующие темы курса математики: «Дифференциальное исчисление функции одного переменного», «Интегральное исчисление функции одной переменной» и «Функции нескольких переменных».
ККР должна быть выполнена в отдельной тетради, на обложке тетради должны быть указаны фамилия студента, его инициалы, полный учебный шифр группы, номер варианта контрольной работы, название дисциплины. В работу должны быть включены все задачи, указанные в задании по варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
Задачи ККР следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью переписать ее условие. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
Чертежи и графики должны быть выполнены с указанием единиц масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже. Для замечаний преподавателя необходимо на каждой странице оставлять поля шириной 2–3 см.
В конце работы должен быть указан список литературы из перечня основной, указанной в данном пособии.
После получения рецензии на сданную на проверку работы студент должен исправить все отмеченные ошибки и недочеты. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента.
Вносить исправления в текст работы после ее рецензирования запрещается.
Студент выполняет вариант контрольной работы, совпадающий с последней цифрой его учебного шифра. Требуется представить решение десяти указанных ниже задач.
График выполнения контрольной работы
| Выдача | Начало семестровых занятий |
| Сдача | Не позднее 10 дней до сессии[1] |
| Контроль | Зачет (Менеджмент) Экзамен (Упр. персоналом) |
Задача 1.
Найти производные функций.
1. а)  ; б)
; б)  ;
;
в)  .
.
2. а)  ; б)
; б) 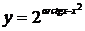 ;
;
в)  .
.
3. а)  ; б)
; б)  ;
;
в)  .
.
4. а)  ; б)
; б) 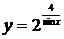 ;
;
в)  .
.
5. а)  ; б)
; б)  ;
;
в)  .
.
6. а)  ; б)
; б)  ;
;
в)  .
.
7. а)  ; б)
; б)  ;
;
в)  .
.
8. а)  ; б)
; б)  ;
;
в)  .
.
9. а)  ; б)
; б)  ;
;
в)  .
.
10. а)  ; б)
; б)  ;
;
в)  .
.
Задача 2.
Исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
1.  . 2.
. 2.  . 3.
. 3. 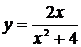 .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7. 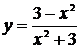 . 8.
. 8.  . 9.
. 9.  .
.
10.  .
.
Задание 3.
Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.
1. а) 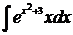 ; б)
; б)  ; в)
; в)  .
.
2. а)  ; б)
; б)  ; в)
; в)  .
.
3. а)  ; б)
; б)  ; в)
; в)  .
.
4. а)  ; б)
; б)  ; в)
; в)  .
.
5. а)  ; б)
; б)  ; в)
; в)  .
.
6. а)  ; б)
; б) 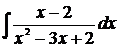 ; в)
; в) 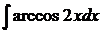 .
.
7. а)  ; б)
; б)  ; в)
; в)  .
.
8. а)  ; б)
; б)  ; в)
; в)  .
.
9. а)  ; б)
; б) 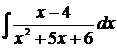 ; в)
; в) 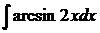 .
.
10. а)  ; б)
; б)  ; в)
; в)  .
.
Задание 4.
Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
Задание 5.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж.
1.  .
.
2.  .
.
3.  (одна полуволна);
(одна полуволна);  .
.
4.  .
.
5.  .
.
В задачах 6–10 вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать чертеж.
6.  .
.
7.  .
.
8. 
9. 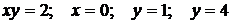 .
.
10.  .
.
Задание 6.
Найти область определения функции двух переменных (дать геометрическое истолкование. Сделать чертеж.).
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5. 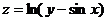 . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 7.
Найти частные производные  ,
,  от функции
от функции  .
.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 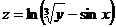 . 10.
. 10.  .
.
Задание 8.
В задачах 1–5 исследовать на экстремум функцию  .
.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
В задачах 6–10 найти наименьшее и наибольшее значения функции  в заданной замкнутой области.
в заданной замкнутой области.
6.  в прямоугольнике
в прямоугольнике  .
.
7.  в треугольнике, ограниченном осями Ох и Оу и прямой
в треугольнике, ограниченном осями Ох и Оу и прямой  .
.
8.  в прямоугольнике
в прямоугольнике  .
.
9.  в области, ограниченной параболой
в области, ограниченной параболой  и осью Ох.
и осью Ох.
10.  в квадрате
в квадрате  .
.
Задание 9.
Вычислить приближенно с помощью полного дифференциала.
1.  . 2.
. 2. 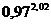 .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6. 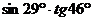 .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
Задание 10.
Инвестор вложил в производство R0 тыс. руб. и в течение n лет планирует непрерывно увеличивать объем инвестиций на a тыс. руб. ежегодно. Ожидаемая доходность инвестиций составляет i% годовых.
Определите:
1) современную стоимость такого проекта по формуле  .
.
2) наращенную сумму такого потока платежей по формуле  .
.
1. R0=11; a=1; n=4; i=1%.
2. R0=12; a=2; n=3; i=2%.
3. R0=13; a=3; n=2; i=3%.
4. R0=14; a=4; n=3; i=4%.
5. R0=15; a=5; n=4; i=5%.
6. R0=16; a=6; n=5; i=6%.
7. R0=17; a=7; n=6; i=7%.
8. R0=18; a=8; n=7; i=8%.
9. R0=19; a=9; n=6; i=9%.
10. R0=20; a=10; n=4; i=10%.
Примеры решения задач
Задача 1.
Найдите производные функций:
а)  ; б)
; б)  ; в)
; в)  .
.
Решение.
а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

б)

в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной  нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно
нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно  :
:

Из последнего уравнения находим  :
:

Задача 2.
Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Исследование функции проведем по следующей схеме:
- Найдем область определения функции.
- Исследуем функцию на непрерывность.
- Установим, является ли функция четной, нечетной.
- Найдем интервалы возрастания и убывания функции и точки экстремума.
- Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
- Найдем асимптоты кривой.
Реализуем указанную схему:
- Функция определена при всех значениях аргумента х, кроме
 .
.
2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах  и
и  . В точке
. В точке  функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
3. Для установления четности или нечетности функции проверим выполнимость равенств  (тогда
(тогда  – четная функция) или
– четная функция) или  (для нечетной функции) для любых х и – х из области определения функции:
(для нечетной функции) для любых х и – х из области определения функции:
 .
.
Следовательно,  и
и  , то есть данная функция не является ни четной, ни нечетной.
, то есть данная функция не является ни четной, ни нечетной.
4. Для исследования функции на экстремум найдем ее первую производную:
 .
.
 при
при  и
и  – не существует при
– не существует при  . Тем самым имеем две критические точки:
. Тем самым имеем две критические точки: 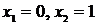 . Но точка
. Но точка  не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.
Разобьем числовую ось на три интервала (рис. 5):  ,
,  .
.
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале – положительна и данная функция возрастает. При переходе через точку  первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:
первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:  . Значит,
. Значит,  – точка минимума.
– точка минимума.

Нарис. 5 знаками +, – указаны интервалы знакопостоянства производной у', а стрелками – возрастание и убывание исследуемой функции.
5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
 .
. 
 при
при  и
и  – не существует при
– не существует при  . Разобьем числовую ось на три интервала (рис. 6):
. Разобьем числовую ось на три интервала (рис. 6):  ,
,  . На первом интервале вторая производная
. На первом интервале вторая производная  отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах  , тем самым график является вогнутым. При переходе через точку
, тем самым график является вогнутым. При переходе через точку 
 меняет свой знак, поэтому
меняет свой знак, поэтому  – абсцисса точки перегиба.
– абсцисса точки перегиба.
Следовательно,  – точка перегиба графика функции.
– точка перегиба графика функции.
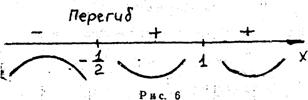
6.  – точка разрыва функции, причем
– точка разрыва функции, причем  . Поэтому прямая
. Поэтому прямая  является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты
является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты  воспользуемся формулами:
воспользуемся формулами:
 .
.
Тогда

При вычислении последнего предела использовалось правило Лопиталя. Значит прямая  есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.
есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 7.

Задание 3.
а1 ) Найти  .
.
Решение. Применяя подстановку  , приведем данный интеграл к табличному интегралу 2. Положим
, приведем данный интеграл к табличному интегралу 2. Положим  , тогда
, тогда  .
.
 .
.
а2) Найти  .
.
Применяя подстановку  , приведем данный интеграл к формуле 10.
, приведем данный интеграл к формуле 10.
Положим  , тогда
, тогда  .
.
 .
.
б) Найти интеграл  .
.
Преобразуем знаменатель дроби, стоящей под знаком интеграла, следующим образом:
 .
.
Тогда после подстановки  получаем
получаем
 =
=

 =
=

При этом при вычислении интеграла  мы воспользовались заменой переменной
мы воспользовались заменой переменной  . Тогда
. Тогда 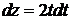 , откуда
, откуда

в1) Найти  .
.
Принимаем  и
и  ; тогда
; тогда 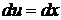 и
и  , следовательно
, следовательно 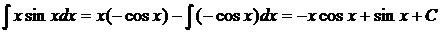 .
.
в2) Найти  .
.
Принимаем  и
и  ; тогда
; тогда  и
и  . Применяя формулу интегрирования по частям, будем иметь:
. Применяя формулу интегрирования по частям, будем иметь:

в3) Найти  .
.
Принимаем 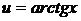 и
и  ; тогда
; тогда  и
и 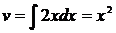 , следовательно,
, следовательно,

Задание 4.
Вычислить площадь фигуры, ограниченной линиями  ,
,  (рис. 8).
(рис. 8).
 Решение. Площадь
Решение. Площадь  фигуры, ограниченной сверху и снизу непрерывными линиями
фигуры, ограниченной сверху и снизу непрерывными линиями  и
и  , пересекающимися в точках с абсциссами
, пересекающимися в точках с абсциссами  и
и  , определяется по формуле
, определяется по формуле
 . (1)
. (1)
Для нахождения точек пересечения данных линий решаем систему уравнений
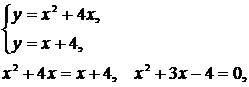
Рис. 8
откуда  . Применяя формулу (1), получим:
. Применяя формулу (1), получим:


Задание 5.
Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной параболой  , прямой
, прямой  и осью Ох.
и осью Ох.
Решение. Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение  или
или  . Легко убедиться, что
. Легко убедиться, что 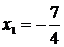 ,
, 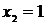 . Первому квадранту соответствует корень
. Первому квадранту соответствует корень 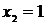 .
.
Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение  , откуда
, откуда  .
.
Таким образом, можно считать, что тело вращения ограничено при  поверхностью, образованной вращением параболы
поверхностью, образованной вращением параболы  вокруг оси Ох, а при
вокруг оси Ох, а при  – вращением прямой
– вращением прямой  .
.
Искомый объем ищем по формуле 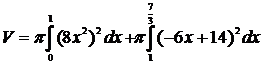 .
.
Для вычисления второго интеграла используем подстановку  . Тогда
. Тогда  и
и  .
.
Отсюда
 .
.

Задание 6.
Найти объем тела, образованного вращением фигуры  ,
,  вокруг оси Ох. (Рис. 9)
вокруг оси Ох. (Рис. 9)
Решение. По формуле (1), учитывая, что 
 получим
получим
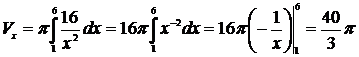 (куб. ед.). Рис. 9
(куб. ед.). Рис. 9
Задание 7.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой  и прямыми
и прямыми  (рис.10).
(рис.10).
Решение. По формуле (2), учитывая, что  ,
,  , получим
, получим
 (куб. ед.).
(куб. ед.).

Задание 8.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, заключенной между линиями  ,
,  (рис.11).
(рис.11).
Решение. Искомый объем определяется разностью 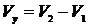 , где
, где  есть объем тела, образованного вращением вокруг оси Оу треугольника АОВ, а
есть объем тела, образованного вращением вокруг оси Оу треугольника АОВ, а  – объем тела, образованного вращением вокруг оси Оу криволинейной трапеции ОтАВ. Чтобы найти пределы интегрирования, найдем ординаты точек пересечения данных линий.
– объем тела, образованного вращением вокруг оси Оу криволинейной трапеции ОтАВ. Чтобы найти пределы интегрирования, найдем ординаты точек пересечения данных линий.
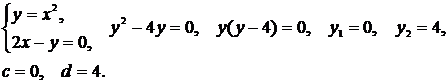
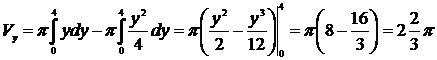 (куб. ед.).
(куб. ед.).
Задание 9.
Исследовать на экстремум функцию
 .
.
Решение. Находим стационарные точки.

Решение последней системы дает 4 стационарные точки:
 .
.
Находим частные производные второго порядка:

Исследуем каждую стационарную точку.
1) В точке  Так как
Так как 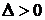 и
и  , то в этой точке функция имеет минимум.
, то в этой точке функция имеет минимум.
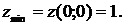
2) В точке 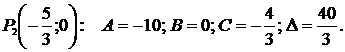 Так как
Так как 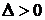 и
и  , то в этой точке функция имеет максимум.
, то в этой точке функция имеет максимум.

3) В точке  Так как
Так как  , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
4) В точке  Так как
Так как  , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
Задание 10.

Найти наибольшее и наименьшее значение функции 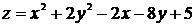 в замкнутом треугольнике АОВ, ограниченном осями координат и прямой
в замкнутом треугольнике АОВ, ограниченном осями координат и прямой  (рис. 12).
(рис. 12).
Решение. Найдем стационарные точки.

Решая систему

находим стационарную точку  . Эта точка лежит внутри области. Вычислим значение функции в этой точке.
. Эта точка лежит внутри области. Вычислим значение функции в этой точке.

Граница заданной области состоит из отрезка О А оси Ох, отрезка ОВ оси Оу и отрезка АВ. Определим наибольшее и наименьшее значение функции 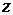 на каждом из этих трех участков. На отрезке ОА
на каждом из этих трех участков. На отрезке ОА  а
а  . При
. При  функция
функция  есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке
есть функция одной независимой переменной х. Находим наибольшее и наименьшее значение этой функции на отрезке  .
.
 ;
;  – стационарная точка.
– стационарная точка.  .
.
Вычислим значения функции на концах отрезка ОА, то есть в точках О и А.  .
.
На отрезке ОВ  и
и  . При
. При  имеем
имеем  . Находим наибольшее и наименьшее значение этой функции
. Находим наибольшее и наименьшее значение этой функции 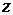 от переменной у на отрезке
от переменной у на отрезке  .
.  ;
;  – стационарная точка.
– стационарная точка.  .
.
Вычислим значения функции 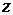 на концах отрезка ОВ, то есть в точках О и В.
на концах отрезка ОВ, то есть в точках О и В.  . Исследуем теперь отрезок АВ. Уравнение прямой АВ:
. Исследуем теперь отрезок АВ. Уравнение прямой АВ:  . Подставив это выражение для у в заданную функцию
. Подставив это выражение для у в заданную функцию 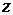 , получим
, получим  или
или  . Определим наибольшее и наименьшее значение этой функции на отрезке
. Определим наибольшее и наименьшее значение этой функции на отрезке  .
.
 ;
;  – стационарная точка.
– стационарная точка.  .
.
Значения функции в точках А и В найдены ранее. Сравнивая полученные результаты, заключаем, что наибольшее значение заданная функция 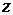 в заданной замкнутой области достигает в точке
в заданной замкнутой области достигает в точке  , а наименьшее значение – в стационарной точке
, а наименьшее значение – в стационарной точке  . Таким образом,
. Таким образом,
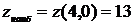 и
и  .
.
Вопросы для подготовки
Дифференциальное исчисление
1. Что называется производной функции одного переменного? Каков ее геометрический, физический и экономический смыслы?
2. Что называется дифференциалом функции одного переменного, каковы его основные свойства?
3. Какая функция называется возрастающей (убывающей)? Каковы необходимый, достаточный признаки возрастания (убывания) функции?
4. Каковы необходимый, достаточные признаки существования экстремума функции?
5. Какая кривая называется выпуклой (вогнутой)? Как найти интервалы выпуклости и вогнутости кривой?
6. Каковы необходимый, достаточный признаки существования точки перегиба?
7. Что называется асимптотой кривой? Как найти вертикальные и наклонные асимптоты?
8. В каком случае и как применяется правило Лопиталя при вычислении пределов?
Интегральное исчисление
1. Понятие первообразной функции. Теоремы о первообразных.
2. Неопределённый интеграл, его свойства
3. Основные правила и формулы интегрирования
4. Метод замена переменной (подстановки)
5. Интегрирование по частям в неопределённом интеграле
6. Разложение рациональной функции на простейшие дроби
7. Интегрирование простейших дробей
8. Интегрирование рациональных функций
9. Интегрирование выражений, содержащих тригонометрические функции
10. Понятие определённого интеграла, его геометрический смысл
11. Основные свойства определённого интеграла
12. Теорема об оценке интеграла
13. Теорема о среднем
14. Теорема Ньютона-Лейбница
15. Замена переменной и интегрирование по частям в определённом интеграле
16. Вычисление площадей плоских фигур
17. Вычисление объемов тел вращения