Теорема о единственности разности: если разность п.р.ч. существует, то она единственна.

ТОМ

1)Определение простой и десятичной дроби:

2)Опр-ие равных дробей:

3)Основное св-во дроби:

Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, то получим дробь равную данной

Когда делим числитель и знаменатель – дробь сокращаем. Для проведения дробей к одинаковому знаменателю – выполняем умножение.

При измерении одного и того же отрезка, мы получили множество равных дробей …. Это множество представляет нам разную запись одного и того же положительного рационального числа (ПРЧ).

Приведение дробей к общему знаменателю – это замена дробей равными им дробями, имеющими одинаковые знаменатели.

Определение. Положительное рациональное число – это множество равных дробей, а каждая дробь, принадлежащая этому множеству, есть запись (представление) этого числа.

Покажем, что множество натуральных чисел является подмножеством множество п.р.ч. N Q₊

(рисуется 2 отрезка) а=2е а=6е₁=6/3е 2 N => N Q₊ Разделим отрезок е на 3 равные части.

4)Опр-ие положительного рационального числа:

Положительным рациональным числом наз. Класс равных дробей,а каждая дробь,принадлежащая этому классу,есть запись этого числа.

5)Опр-ие суммы п.р.ч.;законы сложения:

Сложение положительных рациональных чисел

Определение. Если положительные числа «а» и «в» представлены дробями m/n и p/n, то сумма чисел «а» и «в» называется число, представляемое (m+p)/n

1.Коммуникативный (переместительный) а+в=в+а

2.Ассоциативный (сочетательный) (а+в)+с=а+(в+с)

6)Доказательство переместительного закона сложения:

Коммуникативный (переместительный) а+в=в+а

Дано: а,в ͼ Q+

Док-во: а=m/n в= p/n, где по определению дроби n m p ͼ N, а+в =m/n+p/n= (m+p)/n

в + а = p/n+m/n= (p+m)/n

Рассмотрим 2 дроби

(m+p)/n и (p+m)/n – знаменатели равны

Т.к. числа m и р натуральные, то

m+p= p+m- это переместит закон для натур чисел.

Значит, (m+p)/n=(p+m)/n следовательно а + в = в +а

7)Опр-ия правила п.р.ч.;правила вычитания:

Определение. Разностью положительных рациональных чисел «а» и «в» называется такое число «с», которое удовлетворяет условию а-в=с ó а=в+с

Теорема о существовании: разности п.р.ч. а и в существует, тогда и только тогда, когда в<(или равно)а

Теорема о единственности разности: если разность п.р.ч. существует, то она единственна.

Выведем правило, по которому находят разность «а» и «в»

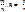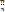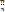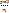Док-во: Пусть а = ; а – в = - = ó(след по опред разности удовлетворяет условию) = + след по опред суммы ↔ m = р + х => (по опред разности натуральных чисел) x = m – p

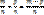
Правило вычитания:

1. Вычитание числа из суммы (а + в) – с = (а – с) + в = а + (в – с)

2. Вычитание суммы из числа а – (в + с) = (а – в) – с = (а – с) – в

8)Опр-ия произведения п.р.ч.;законы умножения:

Определение. Если положительные рациональные чисел представлены дробями 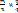то их произведением есть число, представленное дробью

Правило умножения:

1. Переместительный ав = ва

Док-во: а=m/n в= p/q, где по определению дроби n m p q ͼ N,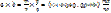

Рассмотрим 2 дроби

и –; nq=qn – перемест. Закон умнож. для натур. чисел

мр=рм- это переместит закон умнож. для натур чисел.

Значит, = следовательно ав = ва

2. Сочетательный (ав)с = а(вс)

3. Умножение суммы на число (а + в)с = ас + вс распределит закон относительно сложен

Умножение разности на число (а – в)с = ас – вс распределит закон относительно вычитанию

9)Опр-ия частного п.р.ч.;правила деления:

Определение. Частным положительных рациональных чисел «а» и «в называется такое число «с», что а = вс, число «с» обозначают как а: в.

Частное чисел m/n и p/q есть mq/np

Док – во: а = m/n; в= p/q;c= mq/np по определению частного а = вс; m/n. p/q.mq/mp= (p (mq))/(q (np)) = (m (pq))/(n (pq))=m\n

m/n ∶ p/q= mq/np

На множестве ПРЧ деление выполняется всегда.

Правила деления:

(ав):с = (а: с)в = а(в: с) деление произведения на число

а: (вс) = (а: в): с = (а: с): в деление числа на произведение

(а + в): с = а: с + в: с деление суммы на число

(а - в): с = а: с - в: с деление разности на число

10)Формулировку теоремы о представлении обычной дроби в виде десятичной:

Теорема. Для того чтобы несократимая дробь , была равной десятичной дроби, необходимо и достаточно, чтобы в разложении ее знаменателя на простые множители входили лишь простые числа 2 и 5.