ВВЕДЕНИЕ
“Инженерная графика” относится к циклу математических и естественнонаучных дисциплин ОПОП ВО и является одной из основных общетехнических дисциплин в системе подготовки кадров высшей квалификации. Студенты приобретают знания, необходимые для изучения других общенаучных и специальных дисциплин.
После изучения дисциплины студент должен:
- приобрести навыки выполнения и чтения чертежей;
- получить знания геометрического моделирования и формообразования сложных форм поверхностей;
- овладеть методами изображения пространственных форм на плоскости и уметь использовать их в профессиональной деятельности;
- уметь принимать эффективные решения при разработке различного рода инженерно-геометрических задач.
Студенты приступают к выполнению контрольной работы после проработки теоретического материала по учебной литературе и нормативной литературе [1-6], по Интернет-ресурсам [7,8].
В случае возникновения трудностей при изучении курса: в понимании теоретического материала, решении задач по темам, выполнении эпюров, студент может получить консультации на кафедре НГ и Г, организуемым в соответствии с графиком. Студенты информируются о консультациях во время установочной сессии, при необходимости индивидуальных консультаций их время должно быть согласовано с ведущим преподавателем: телефон 72-35-64 (деканат ФЗДО) - добавочный 1-71 (кафедра НГ и Г).
ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ
КОНТРОЛЬНЫХ РАБОТ
Контрольные работы по инженерной графике выполняются каждым студентом по индивидуальному варианту, который соответствует последней цифре номера зачетной книжки, на листах чертежной бумаги формата А3 карандашом. При выполнении работ необходимо помнить, что правильное решение может быть получено только при точном выполнении всех графических построений.
При выполнении контрольных работ студенты должны строго соблюдать требования ГОСТов ЕСКД (единой системы конструкторской документации) [7]. В частности, в соответствии с требованиями ГОСТ 2.303-68* основные линии выполняют толщиной 0,6-0,8 мм, тонкие 0,3-0,4 мм. Выбранная толщина линии должна быть одинакова для всех изображений на данном чертеже, вычерчиваемых в одном масштабе.
При выполнении штриховых линий длина штрихов должна быть одинаковой, расстояние между штрихами делают в два-четыре раза меньше длины штриха.
Штрих - пунктирные линии должны пересекаться и заканчиваться штрихами, а не точками. Центр окружности следует отмечать пересечением штрихов. Штрих - пунктирные линии, применяемые в качестве центровых или осевых, следует заменять сплошными тонкими линиями, если диаметр окружности, а также размеры других геометрических фигур в изображении 12 мм и менее.
Надписи и буквенно-цифровые обозначения на листах и в основной надписи выполняют стандартным чертежным шрифтом (ГОСТ 2.304-81) в таблице 1 представлены его основные параметры, на рис.1 приведены цифры и русский алфавит (кириллица).
Таблица 1
| Параметры шрифта | 0боз-начение | Относительный размер | Номер шрифта | |||||||
| 1,8 | 2,5 | 3,5 | ||||||||
| Высота прописных букв | h | h=10d | 1,8 | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14,0 | 20,0 |
| Высота строчных букв | c | 7/10h=7d | 1,3 | 1,8 | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14.0 |
| Расстояние между буквами | a | 2/10h=2d | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 | 2,8 | 4,0 |
| Минимальный шаг строк (высота вспомогательной сетки) | b | 17/10h= 17d | 3,1 | 4,3 | 6,0 | 8,5 | 12,0 | 17,0 | 24,0 | 34,0 |
| Минимальное расстояние между словами | e | 6/10h=6d | 1,1 | 1,5 | 2,1 | 3,0 | 4,2 | 6,0 | 8,4 | 12,0 |
| Толщина линий шрифта | d | 1/10h=d | 0,18 | 0,25 | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 |
Размер шрифта определяется высотой прописных (заглавных) букв и цифр. Высота строчных букв определяется отношением их высоты к номеру шрифта и соответствует предыдущему номеру шрифта. Высота буквы измеряется перпендикулярно к основанию строки. Нижние элементы букв Д, Ц, Щ и верхний элемент буквы Й выполняются за счет расстояний между строками.
Ширинабольшинства прописных букв равна 0,6h или 6d, что примерно соответствует размеру h ближайшего наименьшего номера шрифта.
Исключение составляют буквы А, Д, М, X, Ц, Ы, Ю, ширина которых равна 7d, ширина букв Ж, Ф, Щ, Ш, Ъ принимается за 8d, ширина букв Г, 3, С составляет 5d.
Верхние и нижние элементы строчных букв выполняются за счет расстояний между строками и выходят на величину 3d.
Ширина большинства строчных букв равна 5d. Ширина букв а, м, ц, ъ равна 6d, букв ж, т, ф, ш, щ, ы, ю — 7d, букв з, с — 4d. Ширина большинства цифр 5d, цифры 4 - 6d, цифры 1 - 3 d.
Рекомендуется буквенно-цифровые обозначения и надписи на эпюрах выполнять шрифтом 5 или 3,5; цифровые индексы – шрифтом 1,8 или 2,5.
В табл.2 приведены обозначения, применяемые при оформлении чертежей.
На чертежах должны быть сохранены все построения, обозначены все точки, прямые, плоскости и поверхности, отсутствие таких обозначений на некоторых примерах связано с невозможностью обеспечить хорошее зрительное восприятие материала при незначительных размерах изображений. Примеры, представленные в методических указаниях, не являются образцами, они иллюстрируют компоновку чертежа, при выполнении контрольной работы студент может изменить предложенную компоновку.


Рис. 1 Шрифт типа Б с наклоном
Таблица 2
| Значение | Символ |
| Плоскости проекций | П1 – горизонтальная; П2 – фронтальная; П3 – профильная |
| Оси проекций | x, y, z |
| Точки, расположенные в пространстве | прописные буквы латинского алфавита A, B, C,… или арабскими цифрами 1, 2, 3… |
| Следы прямых | М – горизонтальный след N – фронтальный след |
| Прямые и кривые линии, произвольно расположенные в пространстве по отношению к плоскостям проекций | строчными буквами латинского алфавита a, b, c… |
| Линии уровня | горизонтальная прямая (горизонталь)- h; фронтальная прямая (фронталь)- f; профильная прямая - w. |
| Прямая, например, проходящая через точки А и В | (АВ) |
| Отрезок прямой, например, ограниченной точками А и В | [АВ] |
| Плоскости | прописными буквами греческого алфавита D, H, Ө, S, R, W … |
| Углы наклона к плоскостям проекций | α, β, γ… |
| Углы, например, угол АВС с вершиной в точке В | Ð АВС; |
| Угол между прямой и плоскостью, например, прямой, проходящей через точки АВ и плоскостью γ | Ð(АВ) ˆγ. |
| Расстояние между точками, например, А и В | |АВ| |
| Расстояние точки до плоскости, например, от А до α | |Аα| |
| расстояние между прямыми, например, между «a» и «b» | |ab| |
| Проекции геометрических форм обозначаются теми же буквами (цифрами), что и оригинал, с добавлением индекса плоскости проекций, на которой они получены: горизонтальные проекции фронтальные проекции профильные проекции | A1, B1, 11, 21, a1, b1, α1, β1, γ1, А1, Β1, Δ1; A2, B2, 12, 22, α2, β2, γ2, А2, Β2, Δ2; A3, B3,13, 23, a3, b3, α3, β3, γ3, А3, Β3, Δ3. |
| Совпадают, равны | º |
| Подобны | ~ |
| Перпендикулярны | ^ |
| Скрещиваются | · 
|
| Параллельны | || |
| Принадлежит, является элементом множества | Î |
| Включает, содержит | Ì |
| Пересечение множеств | ∩ |
| Логическое следствие | => |
На каждом листе текстового и графического документа выполняется рамка, на всех листах, кроме титульного, вычерчивается и заполняется основная надпись. Каждую текстовую и графическую работу оформляют на отдельном формате. На рис. 2 представлена схема размещения рамки и основной надписи:

Рис.2
Контрольные работы в сброшюрованном виде должны быть представлены на кафедру в сроки строго соответствующие графику выполнения работ, установленным деканатом. Каждая контрольная работа должна включать все листы, предусмотренные содержанием. При неверном выполнении чертежей преподаватель делает замечания, которые должны быть исправлены там же или, если указано, переделаны на новых листах. Замечания, сделанные при рецензировании, удалять с листа нельзя. К выполнению второй контрольной работы необходимо приступать, не дожидаясь ответа на первую.
Защита контрольных работ проводится при устном собеседовании на практических занятиях во время сессии. Преподаватель вправе аннулировать представленную контрольную работу, если убеждается, что она выполнена не самостоятельно или скопирована.
К экзамену (зачету) допускаются студенты, у которых зачтены предусмотренные программой контрольные работы и выполнены аудиторные работы.
СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ№1
1. Титульный лист и содержание.
2. Метрические и позиционные задачи.
3. Перпендикуляр к плоскости. Взаимное положение прямой и плоскости, многогранника, поверхности вращения.
СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ№2
1. Построение трех видов детали по данному наглядному изображению.
2. Построение трех изображений по двум заданным. Выполнение разрезов и сечений.
3. Построение аксонометрической проекции детали.
4. Изображение и обозначение резьб, соединений на резьбе, изображение и обозначение
крепежных деталей.
Контрольная работа № 1
Перед выполнение листов 2, 3 студенту необходимо изучить следующие темы [1,2]:
· Метод ортогонального проецирования.
· Точка на эпюре Монжа, задание линии и плоскости на комплексном чертеже Монжа.
· Взаимное положение геометрических форм.
· Методы преобразования чертежа
Для того чтобы успешно решить задачи студент должен знать ответы на вопросы:
- В чем заключается сущность метода ортогонального проецирования?
- Какими координатами определяются проекции точки на П1, П2 , П3?
3. Как расположены по отношению к плоскостям проекций прямые общего положения? Линии уровня? Проецирующие прямые?
4. Каковы особенности эпюр прямых общего положения? Линий уровня? Проецирующих прямых?
- Какие существуют взаимные положения прямых в пространстве? Как на эпюре определить взаимное положение прямых?
- Каковы условия проецирования прямого угла в истинную величину?
7. Какими способами задают плоскость в пространстве?
8. Какие плоскости называют плоскостями общего положения; проецирующими; плоскостями уровня?
9. Каковы свойства эпюр плоскостей общего положения; частного положения?
- Каковы условия принадлежности точки и прямой плоскости?
- Как прямая может быть расположена по отношению к плоскости? Как расположены проекции прямой перпендикулярной к плоскости общего положения?
- Сформулируйте алгоритмы определения взаимного положения прямой и плоскости общего положения.
- Конкурирующие точки и их использование для определения видимости. Как устанавливается относительная видимость прямой и плоской фигуры?
ЛИСТ 1: Титульный лист и содержание
Перед выполнением первого студенту необходимо ознакомиться с ГОСТами 2.304-81*, 2.105-79*, 2.104-2006 [7]. На рис.3 представлен пример выполнения этого листа. Работа выполняется на двух листах формата А4, рекомендуется выделить эти форматы на листе А3, не разрезая его.
Титульный лист выполняется в соответствии с требованиями, предъявляемыми к текстовым документам ГОСТ 2.105-79*, к чертежным шрифтам ГОСТ 2.304-81 [7].
Рекомендуется следующая последовательность выполнения надписей стандартным шрифтом:
1- размещают текст на листе. Для этого определяют суммарную длину строки текста, при выбранном размере шрифта. Если размер строки получается больше, чем место, предназначенное для надписи, меняют размер шрифта или разбивают текст на большее количество строк. Затем определяют положение начала строки, исходя из требуемой компоновки листа;
2- выполняют вспомогательную сетку в виде тонких линий, ограничивающих строку по высоте, каждую букву по ширине, определяющую положение наклонных и горизонтальных элементов шрифта. Перед разбивкой сетки определяют случаи изменения расстояния между буквами в тексте. Если в слове, написанном прописными буквами, встречаются сочетания Г и А, Г и Д, Г и Л, Т и А, Т и Л, Ь и Т, Р и А, Р и Д - промежуток между ними уменьшают вдвое, так же поступают и в том случае, если буква А стоит в середине слова. Наличие тире в тексте требует увеличения расстояния между словами. Если слова в тексте разделены знаком препинания, то минимальное расстояние между словами измеряется от знака до следующего за ним слова. Сетку для шрифта выполняют твердым карандашом без нажима, накалывать сетку измерительным инструментом нельзя;
3- заполняют сетку. Буквы и цифры выполняют, допуская движение руки только в двух направлениях - сверху вниз и слева направо. Для всего текста, выполненного одним размером шрифта, толщина линий обводки должна быть одинакова для прописных и строчных букв. При этом рекомендуется следить, чтобы грифель карандаша давал линии одной толщины.
Рис.3 Титульный лист и содержание
Наличие навыка выполнения надписей стандартным шрифтом может позволить отказаться от выполнения подробной вспомогательной сетки и ограничиться выполнением двух параллельных горизонтальных линий, с расстоянием между ними, равным высоте букв, а также наклонных линий в начале, конце и середине строки, для контроля наклона.
Основная надпись выполняется в соответствии с требования ГОСТ 2.104-2006 «Основные надписи». Располагается в правом нижнем углу конструкторских документов. Пример и размеры основных надписей для чертежей и схем и для текстовых конструкторских документов представлены на рисунке 4.

Рис. 4
Основная надпись на первом листе текстовых документов, в нашем случае, на листе «Содержание», выполняется 185х40 мм. Основная надпись для первого листа чертежей - 185х55 мм.
Пример заполнения основной надписи к контрольной работе приведен на рис.3, 4. Подписи, дата сдачи работы выполняются ручкой.
ЛИСТ 2: Метрические и позиционные задачи
Задачи 1, 2, 3
Метрическими задачами называют задачи связанные с определением или построением натуральных размеров, углов наклона отрезков и плоских фигур, позиционными – с определением взаимного положения геометрических форм. Пример компоновки представлен на рис. 5, на листе решаются три задачи:
При оформлении эпюра должны быть сохранены все промежуточные построения тонкими линиями толщиной 0,1-0,2 мм; линии видимого контура выполняют сплошными основными линиями толщиной 0,6-0,8 мм; невидимый контур показывают штриховыми линиями толщиной 0,3-0,4 мм. Нумерация задач в кружках диаметром 10 мм шрифтом №5. Проекции всех точек, линий и плоскостей необходимо подписать, вспомогательные секущие плоскости обозначить разомкнутой линией.
задача 1: определить натуральную величину отрезка и углов наклона его к плоскостям
проекций.
задача 2: определить натуральную величину плоскости методом замены плоскостей
проекций.
задача 3: определить взаимное положение прямой и плоскости
Таблица 3
| Вариант | Координаты точек | |||||||||||||||||||
| А | В | С | D | M | N | |||||||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | |||
Рекомендации по решению задачи №1
По исходным данным, приведенным в таблице 3, строят горизонтальную и фронтальную проекции отрезка MN.
Определить натуральную величину отрезка прямой можно, когда прямая является линией уровня, т.е. параллельна одной из плоскостей проекций. В этом случае на ту плоскость проекций, которой она параллельна, прямая будет проецироваться без искажения. Рассмотренный в примере выполнения (рис. 5) отрезок является прямой общего положения, следовательно, для того, чтобы определить натуральную величину заданного отрезка необходимо воспользоваться методами преобразования чертежа.
Существует несколько способов определения натуральной величины отрезка прямой: метод плоскопараллельного перемещения; метод вращения; метод прямоугольного треугольника; метод замены плоскостей. Студент при выполнении данного задания может воспользоваться любым из вышеперечисленных способов. В рассматриваемом примере натуральная величина отрезка определена методом замены плоскостей (Рис. 5).
Здесь же определены и углы наклона отрезка MN к плоскостям проекций α и β. При определении углов α и β следует помнить, что линия тригонометрического нуля проводится параллельно оси, угловое направление показывается от линии тригонометрического нуля, а за положительное направление угла принимается направление против часовой стрелки от линии тригонометрического нуля.
Рекомендации по решению задачи №2
По исходным данным, приведенным в таблице 3, строят горизонтальную и фронтальную проекции плоскости АВС.
Определить величину плоской фигуры на эпюре можно, если она является плоскостью уровня, то есть, параллельна одной из плоскостей проекций и перпендикулярна к остальным. При этом на ту плоскость проекций, которой фигура параллельна, она проецируется без искажения, а на другие в виде прямой параллельной к оси, разделяющей эти плоскости.
Рассмотренная на рис.5 плоскость треугольника АВС является плоскостью общего положения – она не параллельна и не перпендикулярна ни одной из плоскостей проекций и на все плоскости проекций проецируется с искажением. Для ее преобразования в плоскость уровня при любом способе решения задачи сначала производят ее преобразование в проецирующую плоскость - перпендикулярную к одной из плоскостей проекций и не параллельную к остальным. Такая плоскость проецируется на ту плоскость проекций, к которой она перпендикулярна в виде наклонной ко всем осям прямой, а на другие плоскости проекций с искажением. Затем плоскость преобразуют в плоскость уровня – параллельную к одной из плоскостей проекций и перпендикулярную к остальным.
В примере (рис.5) используется метод замены плоскостей проекций, при его применении должны соблюдаться два условия:
- новая плоскость проекций должна быть перпендикулярна к оставшейся плоскости проекций;
- геометрическая форма должна занять по отношению к новой плоскости проекций частное положение, то есть быть к ней параллельна, или перпендикулярна.
В этом случае, для построения новой проекции любой точки от новой оси, разделяющей плоскости проекций, по линии связи откладывают координату точки с той плоскости проекций, которую заменяют.
Алгоритм преобразования плоскости общего положения в плоскость уровня:
в плоскости строят одну из главных линий плоскости - горизонталь или фронталь ей принадлежащую.
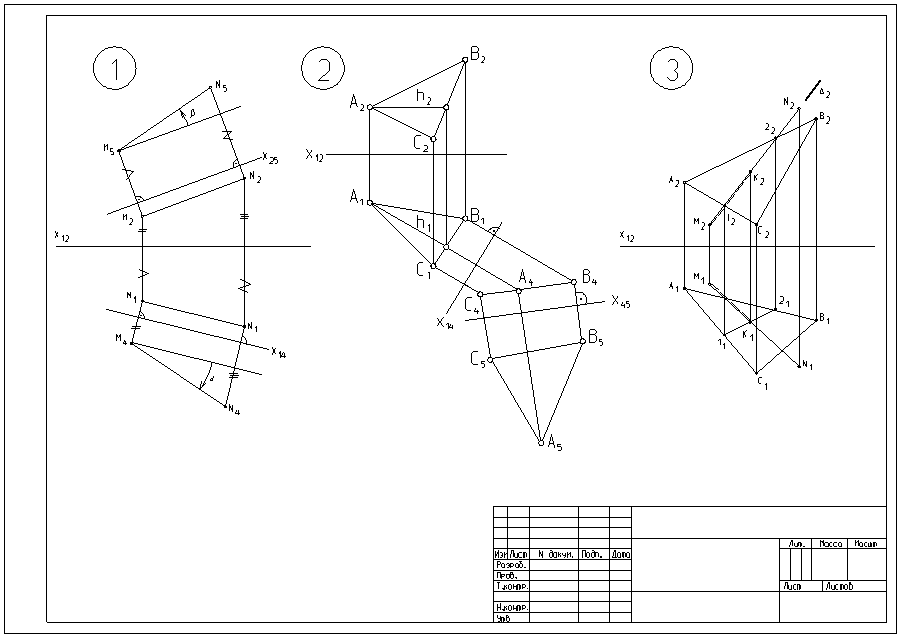
Рис. 5
Фронталь и горизонталь (линии уровня) - это прямые, параллельные соответственно фронтальной и горизонтальной плоскости проекций и наклонные к остальным. Эти прямые проецируются в истинную величину на ту плоскость, которой они параллельны, а на другие – в виде линий параллельных осям, разделяющим эти плоскости. Так как h2||x12; f1||x12, построение горизонтали начинают с фронтальной проекции, а фронтали – с горизонтальной проекции. В случае если одна из сторон плоскости является линией уровня, дополнительного построения такой линии не требуется, ее нужно только обозначить на эпюре.
В примере (рис.5) горизонталь построили через точку А.
1- преобразуют плоскость общего положения в проецирующую: вводят новую плоскость проекций, в примере на рис.5 p4 ^ p1, АВС^ p4. При этом ось x14^h1. Для построения проекции, вырождающейся в прямую наклонную к оси x14, от новой оси по линиям связи откладывают координаты точек с той плоскости, которую заменяют – координаты ZА, ZВ, ZС измеряемые от А2, В2, С2 до оси x12.
2- преобразуют проецирующую плоскость в плоскость уровня: вводят новую плоскость π5^π4, АВС|| π5. При этом новая ось x45 параллельна проекции А4В4С4.
Рекомендации по решению задачи №3
По исходным данным, приведенным в таблице 3, строят горизонтальную и фронтальную проекции плоскости АВС и отрезка MN. В задаче необходимо определить взаимное положение прямой MN и плоскости АBC. Относительно плоскости прямая может занимать три разных положения: прямая может принадлежать плоскости, прямая может быть параллельна плоскости и прямая может пересекать плоскость (как частный случай пересечения- прямая может быть перпендикулярна плоскости). Прямая принадлежит плоскости, если имеет с плоскостью две общие точки или одну общую точку и параллельна прямой, лежащей в этой плоскости. Прямая параллельна плоскости, если она параллельна некоторой прямой лежащей в этой плоскости. Прямая пересекает плоскость (т.е. имеет с плоскость одну общую точку), если она пересекает некоторую прямую, лежащую в этой плоскости. Для определения взаимного положения прямой и плоскости необходимо использовать вспомогательную секущую плоскость.
1 этап - прямую (MN) заключают во вспомогательную, обычно проецирующую плоскость, строят линию пересечения заданной и вспомогательной плоскостей. Использование в качестве вспомогательной именно проецирующей плоскости, (перпендикулярной к одной из плоскостей проекций), связано с тем, что проекции плоскости и прямой, помещенной в эту плоскость, совпадут (при использовании горизонтально-проецирующей плоскости – горизонтальные, фронтально-проецирующей плоскости – фронтальные). Строят проекции линии пересечения заданной и вспомогательной плоскостей на другой плоскости проекций. Затем, рассматривая взаимное положение построенной проекции линии пересечения плоскостей и заданной прямой, делают вывод о положении прямой относительно заданной плоскости.
На рис.5 рассмотрен пример использования фронтально-проецирующей плоскости Δ. Строят линию пересечения заданной плоскости АВС и вспомогательной Δ, на рис.5 это отрезок 1-2. Определяют взаимное положение проекций MN и 1-2, на рассматриваемом примере это M1N1 и 1121.Так как проекции этих линий пересекаются, в данном случае, в К1, делаем вывод - прямая MN пересекается с плоскостью АВС в точке К.
2 этап - методом конкурирующих точек определяют видимость проекций перпендикуляра.
Выбирают конкурирующую точку – точку мнимого пересечения скрещивающихся прямых, строят проекции этих двух точек на другой плоскости проекций и сравнивают их координаты. Точка, имеющая бóльшую координату, принадлежит видимой линии. Если определяют видимость на горизонтальной плоскости, то сравнивают значение координаты Z, для определения видимости на фронтальной плоскости – Y.
ЛИСТ 3: Перпендикуляр к плоскости. Взаимное положение прямой
с плоскостью, многогранником, поверхностью вращения.
Задачи 4, 5, 6
На рис. 6 приведен пример компоновки листа 3. Требования к оформлению листа 3 аналогичны требованиям к оформлению листа 2.
Задача 4: Определить расстояние от точки D до плоскости АВС.
По исходным данным, приведенным в таблице 3, строят горизонтальную и фронтальную проекции точки D и плоскости АВС.
Рекомендации по решению задачи №4
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Решение задачи разбивается на 4 этапа:
1 этап– из точки D нужно опустить перпендикуляр b на плоскость АВС.
Известно, что если прямая (например, b) перпендикулярна к плоскости, то ее горизонтальная проекция (b1) перпендикулярна горизонтальной проекции горизонтали (h1), фронтальная проекция прямой (b2) перпендикулярна фронтальной проекции фронтали (f2), т.е. b1^h1, b2^ f2. Поэтому, чтобы построить прямую b, сначала необходимо построить любую горизонталь h и фронталь f, принадлежащие плоскости АВС.
На примере (рис.6) фронталь построили через точку А, горизонталь - через С. Использование этих точек, при заданных условиях, позволяет уменьшить количество построений: т.к. любая прямая строится через 2 точки, то рационально использовать уже имеющиеся на чертеже точки плоскости.
2 этап – необходимо определить точку пересечения перпендикуляра (b) с плоскостью АВС. На данном этапе задача решается аналогично задаче 3, где определялась точка пересечения прямой MN и плоскости треугольника ABC.
На рис.6 рассмотрен пример использования фронтально-проецирующей плоскости Δ. Строят линию пересечения заданной плоскости АВС и вспомогательной Δ, на рис.6 это отрезок 3-4. Определяют взаимное положение проекций b и 3-4, на рассматриваемом примере это b1 и 3141.Так как проекции этих линий пересекаются, в данном случае, в К1, делаем вывод - прямая b пересекается с плоскостью АВС в точке К.
3 этап - методом конкурирующих точек определяют видимость проекций перпендикуляра.
На рис.6 для определения видимости прямой на фронтальной плоскости используют конкурирующую точку между перпендикуляром DК и стороной плоскости АС, на горизонтальной– между DК и СВ.
4 этап – определяют натуральную величину отрезка.
Анализируя положение проекций этого отрезка на плоскостях проекций, делаем вывод о его положении в пространстве. Если он является прямой общего положения, необходимы дополнительные преобразования, т.к. ни одна проекция не является истинной величиной. В примере (рис.6) использован способ прямоугольного треугольника. На любой плоскости проекций строим прямоугольный треугольник, один его катет это проекция отрезка, другой - разность координат концов отрезка - DZ или DY, измеренная на другой плоскости проекций. Гипотенуза этого прямоугольного треугольника – натуральная величина отрезка. Длину отрезка определили, построив на горизонтальной плоскости прямоугольный треугольник К1D1D0, где D1D0– разность координат DZ (проекций К2 и D2), К1D0 – расстояние от точки D до плоскости АВС.



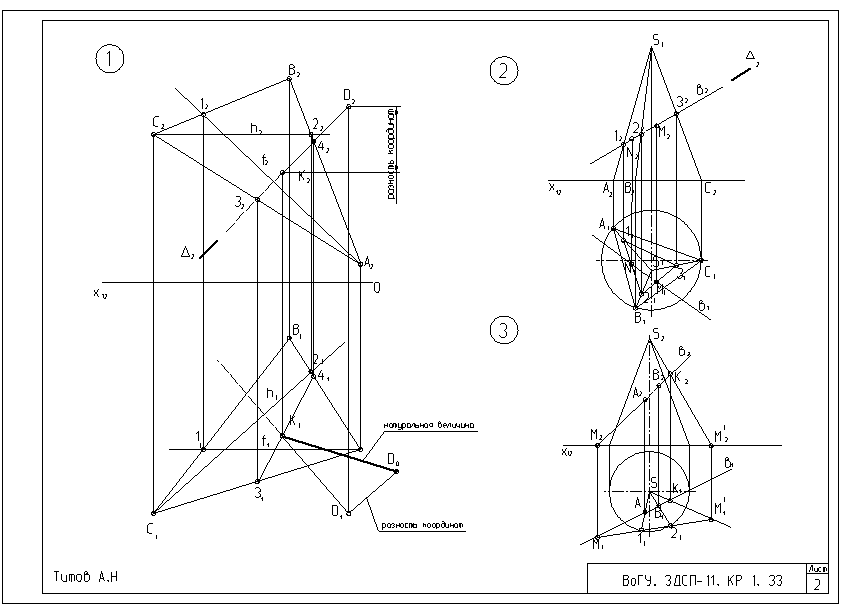
Рис. 6 Задачи 4, 5, 6
Задача 5:
Определить взаимное положение прямой и трехгранной пирамиды.
Положение прямой (восходящая или нисходящая) студент выбирает самостоятельно, учитывая характеристику прямой по таблице 4. Трехгранная пирамида для всех вариантов имеет высоту 70 мм, ее основание произвольно вписывается в окружность диаметром 60, контуры пирамиды и положение прямой не должны быть копией рассмотренного на рис.6 примера.
Таблица 4
| Вариант | Характеристика прямой к задаче 5 | Характеристика прямой к задаче 6 |
| Общего положения | Фронталь под углом 60° к π1 | |
| Фронталь под углом 45° к π1 | Общего положения | |
| Горизонталь под углом 60° к π2 | Общего положения | |
| Общего положения | Фронталь под углом 45° к π1 | |
| Фронталь под углом 30° к π1 | Общего положения | |
| Горизонталь под углом 45° к π2 | Фронталь под углом 60° к π1 | |
| Общего положения | Фронталь под углом 45° к π1 | |
| Фронталь под углом 60° к π1 | Фронталь под углом 30° к π1 | |
| Горизонталь под углом 30° к π2 | Общего положения | |
| Общего положения | Фронталь под углом 30° к π1 |
Рекомендации по решению задачи 5
Как и определение взаимного положения прямой и плоскости, так и установление расположения в системе прямая – многогранник выполняется заключением прямой в дополнительную, чаще всего, проецирующую плоскость. В рассмотренном на рис.6 примере, использована фронтально проецирующая плоскость Δ. Затем строят линию сечения многогранника этой вспомогательной плоскостью по точкам пересечения с ребрами (на рис.6 – точки 1, 2, 3).
При рассмотрении взаимного положения проекций прямой и сечения делается вывод о взаимном положении пирамиды и прямой. В примере горизонтальная проекция прямой (b1) пересекается с проекцией сечения (112131) в N1 и M1, т.е. точки M, N одновременно принадлежат прямой b и поверхности пирамиды, и являются точками пересечения прямой и многогранника. Затем методом конкурирующих точек определяют видимость проекций прямой.
Задача 6: Определить взаимное положение прямой
и прямого кругового конуса.
Во всех вариантах решают задачу для прямого кругового конуса высотой 65мм и диаметром основания 60мм, прямую задают в соответствии с характеристикой, указанной в таблице 4.
Задача решается на основе того же алгоритма, что и две предыдущих, при этом выбирать вспомогательную секущую плоскость нужно так, чтобы получить в сечении конуса окружность или треугольник – наиболее простые для построения формы.
В рассмотренном на рис.6 примере задана линия общего положения, в отличие от задачи 1 и 2, использование проецирующей плоскости не даст простого решения, в сечении получатся плоские фигуры, ограниченные кривыми 2-го порядка.
Чтобы получить в сечении треугольник, используется вспомогательная плоскость общего положения. Плоскость общего положения задают пересекающимися прямыми – заданной линией (b) и произвольной прямой, проходящей через вершину конуса. Точку пересечения линий выбирают произвольно на прямой b (в примере - это точка К). Выбранная вспомогательная плоскость отсекает от конуса треугольник, проходящий через точки S, 1, 2. При рассмотрении взаимного положения проекций треугольника сечения (S11121) и прямой (b1) получаем, что прямая пересекает коническую поверхность в точках А и В.
На эпюре необходимо определить видимость проекций прямой.
Контрольная работа № 2
ЛИСТ 1: Виды
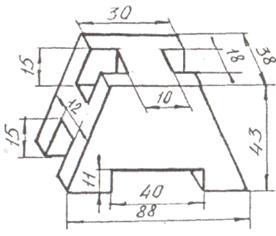
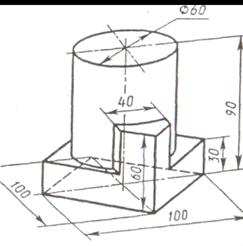
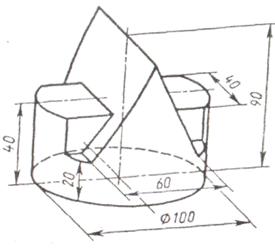
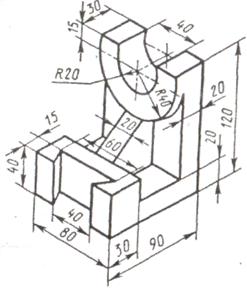
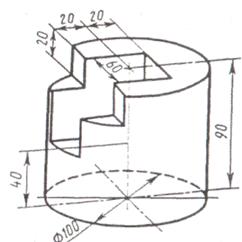
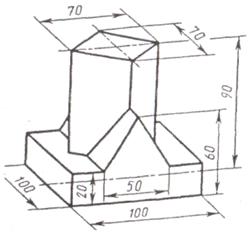
Задание. Построить три вида детали по данному наглядному изображению в аксонометрической проекции. Проставить размеры. Пример выполнения приведен на рис.7. Индивидуальные задания даны в таблицы 5. Работу выполнить на формате А3.

 Таблица 5
Таблица 5
0 1
 | |||
 | |||






 | |||
 | |||

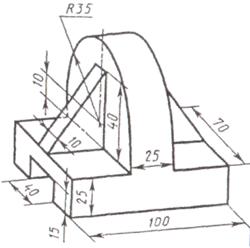
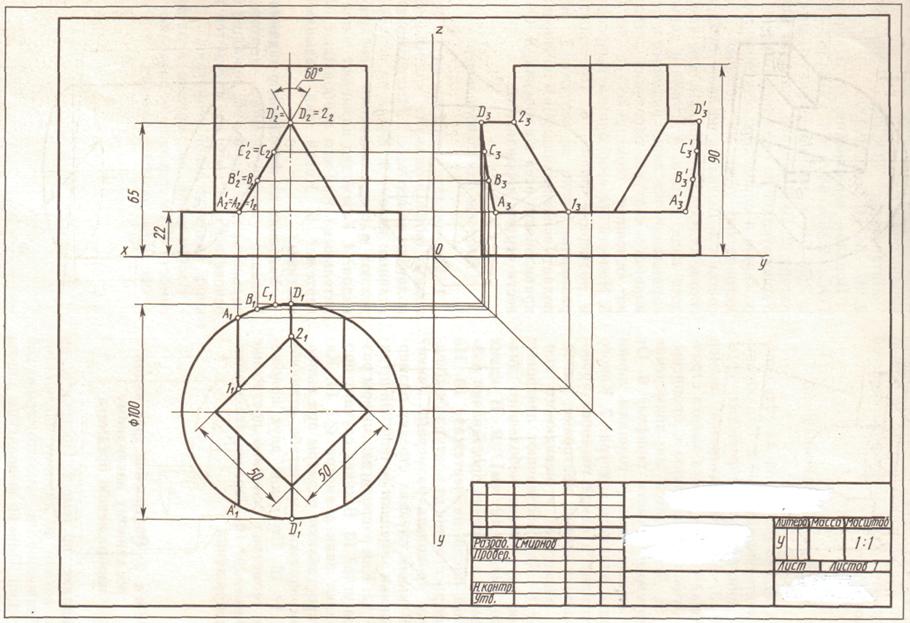
Рис. 7
Вид – это изображение наружной, обращенной к наблюдателю видимой части предмета, полученное методом ортогонального проецирования. Линии невидимого контура на чертеже показываются штриховыми линиями.
Виды делят на основные, дополнительные и местные.
Основные виды - изображения видимой части предмета на основные плоскости проекций. Изобр<