Т. Крамера и её формулы.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
? = det (ai j)
и n вспомогательных определителей? i (i=), которые получаются из определителя? заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
?? x i =? i (i =). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i =? i /?.
Если главный определитель системы? и все вспомогательные определители? i = 0 (i=), то система имеет бесчисленное множество решений. Если главный определитель системы? = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Метод Гаусса, решение системы линейных ур-ний.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
Расширенная матрица этой системы имеет вид
Метод Гаусса основывается на следующих утверждениях.
I. Системы уравнений, полученные в результате следующих преобразований:
перестановка уравнений;
умножение уравнения на любое число. отличное от нуля;
прибавление одногоуравнения, умноженного на любое число, к другому уравнению,
являются эквивалентными, т.е. имеют одни и те же решения.
II. Преобразованиям уравнений системы, очевидно, соответствуют элементарные преобразования строк расширенной матрицы системы:
перестановка строк;
умножение всех элементов строки на любое число. отличное от нуля;
прибавление элементов одной строки, умноженных на одно и то же число, к соответствующим элементам другой строки.
Матрицы A и B, полученные одна из другой с помощью элементарных преобразований строк, называются эквивалентными, что обозначается A? B.
Чтобы решить систему n уравнений с n неизвестными, нужно расширенную матрицу системы с помощью элементарных преобразований строк привести к такому виду, чтобы основная матрица системы (стоящая слева от черты)
Метод Гаусса является наиболее широко распространенным методом решения задач линейной алгебры; как вы увидите в дальнейшем, с его помощью решаются самые разные задачи.
Дана система линейных алгебраических уравнений (СЛАУ) с неизвестными. Требуется решить эту систему: определить, сколько решений она имеет (ни одного, одно или бесконечно много), а если она имеет хотя бы одно решение, то найти любое из них.
Формально задача ставится следующим образом: решить систему:
где коэффициенты и известны, а переменные - искомые неизвестные.
Удобно матричное представление этой задачи:
где - матрица, составленная из коэффициентов, и - векторы-столбцы высоты.
Стоит отметить, что СЛАУ может быть не над полем действительных чисел, а над полем по модулю какого-либо числа, т.е.:
- алгоритм Гаусса работает и для таких систем тоже (но этот случай будет рассмотрен ниже в отдельном разделе).
Обратная матрица и её вычисление.
Определение. Матрица В называется обратной по отношению к матрице А, если
.
Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.
Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.
Определение. Матрица имеющая обратную матрицу называется обратимой.
Теорема. Если квадратная матрица А имеет обратную, то она единственная.
Доказательство. Пусть В и С - две матрицы обратные к матрице А. Тогда и. Имеем,
, ч.т.д.
7. Матричный метод, решение системы линейных ур-ний
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с 
неизвестными (над произвольным полем):
Тогда её можно переписать в матричной форме:
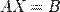, где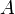 
— основная матрица системы, 
и 
— столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на 
— матрицу, обратную к матрице :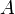 
Так как 
, получаем 
. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
.
Для однородной системы линейных уравнений, то есть когда вектор 
, действительно обратное правило: система 
имеет нетривиальное (то есть ненулевое) решение только если 
. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Введем матрицу системы
и матрицы 
и 
. Пусть 
.
Представим систему (1.10) в виде матричного уравнения АХ=В. Это легко проверить, перемножив матрицы А и Х.
Действительно,
Решим теперь матричное уравнение А·Х=В. Умножим обе части уравнения на матрицу А-1 слева. Тогда А-1·А·Х = А-1·В, а так как
А-1·А=Е, то имеем Е·Х=А-1·В и, наконец,
Х = А-1·В