При освещении тонкой плоскопараллельной плёнки или пластинки с показателем преломления n происходит наложение двух световых волн, возникающих в результате деления падающей волны. Первая из них образуется в результате отражения от передней поверхности пленки в точке А (луч 1 на рис 2). Вторая волна образуется в результате преломления исходной волны,
отражения от задней поверхностей плёнки в точке В и последующего преломления в точке С (луч 2). Для плоскопараллельной пластинки постоянной толщины, равной d, интерференционная картина наблюдается в фокальной плоскости линзы, собирающей лучи 1 и 2.
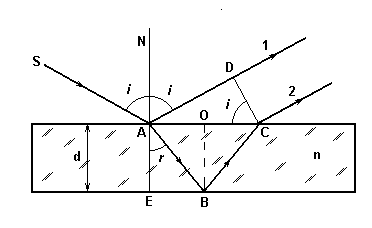
Рис.2. Интерференция света в тонкой пленке.
До точки А оптическая разность хода между этими лучами отсутствует. Оптическая длины пути луча 1 от точки А до точки D составит L1 = nв AD + λ/2 (nв - показатель преломления воздуха; будем считать, что nв = 1). Дополнительное слагаемое λ/2 возникает из-за того, что, отражение волны в точке А происходит от оптически более плотной среды (т.е. от среды с более высоким показателем преломления). В этом случае фаза отраженной волны скачкообразно изменяется на π. Это можно представить как рост оптической длины пути луча 1 на величину, равную половине длины волны в вакууме. Так как при отражении волны от оптически менее плотной среды (отражение в точке В от воздуха) изменения фазы не происходит, то оптическая длина пути луча 2 равна L2 = n(AB + ВС). Линза не вносит дополнительной разности хода для параллельных лучей, исходящих из точек, лежащих в одной плоскости, перпендикулярной этим лучам. Линза лишь преобразует плоскую волну в сходящуюся сферическую волну. Поэтому разность хода между лучами 1 и 2, исходящими из точек C и D, не изменится в точке наложения лучей Р.
Оптическая разность хода, возникающая между лучами 1 и 2 от источника S до точки наложения лучей Р будет равна
Δопт = L 2 - L1 = n (АВ + ВС) - (AD + λ /2).
Отсюда имеем:
Δопт = 2nАВ - AD – λ /2 (6)
Из треугольников ABО и ADC следует, что
AD = AC sin i, AC = 2АО = 2d tg r, AD = 2d sin i tg r; АВ = d / cos r
Подставив два последние выражения в (6), получим:
Δопт = 2nd/cos r – 2d tg r sin i – λ /2 (7)
По закону преломления света на границе двух сред sin i = n sin r, тогда
sin r = sin i / n; cos r =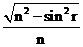 
, tg r = 
.
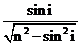Подставив два последних выражения в (7), после простых преобразований получим:
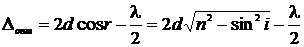
Пусть плоскопараллельная пластинка (d = const) освещается монохроматическим рассеянным светом (что обеспечивает различные углы падения i). Для некоторого угла падения величина Δопт для лучей 1 и 2 будет одинаковой независимо от положения точки А на поверхности пластины,. При наложении пар лучей от всей поверхности пластинки с помощью линзы будут наблюдаться интерференционные полосы, каждая из которых соответствует одному и тому же углу падения. Поэтому их называют полосами равного наклона. Они имеют вид чередующихся концентрических светлых и темных колец. Если толщина пластинки не постоянна (например, клинообразная пластинка), то при освещении ее параллельным пучком лучей (т.е. при одном и том же угле падения i = const) для лучей, отраженных от обеих поверхностей, условия максимума или минимума выполняются для определенных участков с одинаковой толщиной. Светлые или темные полосы, образованные при отражении света участками пластины с одинаковой толщиной, поэтому называют интерференционными полосами равной толщины. Для клиновидной пластинки они имеют вид прямоугольных светлых и темных полос, параллельных ребру.
Кольца Ньютона.
Частный случай полос равной толщины - кольца Ньютона - наблюдаются, если плосковыпуклую линзу поместить на плоскопараллельную стеклянную пластинку (рис 3).
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от воздуха в точке А и от стекла в точке В (т.е. от верхней и нижней границ воздушной прослойки), оказываются когерентными и интерферируют. Волна, отраженная от плоской поверхности линзы, не когерентна с ними и дает лишь равномерную засветку. Точки, для которых толщина воздушного зазора одинакова, располагаются на окружностях, поэтому интерференционная картина имеет вид чередующихся концентрических темных и светлых колец.
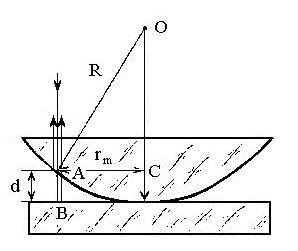
Рис.3. Схема возникновения колец Ньютона
Так как отражение световой волны в точке В происходит от стекла (оптически более плотной среды), то оптическая длина пути второго луча в точке А составит АВ + ВА + λ/2. Оптическая длина пути первого луча в точке А равна нулю. Поэтому
Δопт = L2- L1 = АВ + ВА + λ/2 = 2d + λ / 2
Тёмные кольца образуются там, где оптическая разность хода равна нечётному числу полуволн:
Δопт = 2d + λ /2 = (2m + 1) λ /2,
т.е. при толщине зазора
d = m λ /2, (8)
где m = 0,1,2,3... - номер кольца.
В центре интерференционной картины находится темный круг, соответствующий минимуму нулевого порядка. Если rm - радиус темного кольца под номером m, то из треугольника AОС (см. рис.3) имеем:
rm2 = R2 - (R - d,)2 = 2Rd – d 2, (9)
где R - радиус кривизны линзы. Полагая величину воздушного зазора в месте возникновения колец малой, (т.е. пренебрегая d 2 по сравнению с 2Rd), получим:
rm 2 = 2Rd..
Подставляя сюда (8), получим
rm2 = Rmλ (10)
Из этой формулы видно, что зная длину волны используемого света радиус кривизны линзы можно найти путем измерения радиуса кольца Ньютона и определения его порядкового номера.
Использование формулы (10) для определения радиуса кривизны может привести к ошибке, т.к. в точке соприкосновения линзы и стеклянной пластинки возможна деформация, как линзы, так и пластинки, сравнимая по величине с длиной волны света. Поэтому результаты, полученные без учета этого факта, являются неточными.
Величина воздушного зазора оказывается меньше теоретической величины, полученной из рис.3, на величину суммарной деформации стеклянной пластинки и линзы δ (рис.4). Учитывая это, в формулу (9) вместо толщины воздушного зазора d необходимо подставить сумму толщины воздушного зазора и величины суммарной деформации линзы и стеклянной пластинки (d + δ):
rm2 = R2 – [R –(d+ δ)]2.
Пренебрегая малой величиной (d+ δ)2, получаем:
rm2 = 2R(d + δ)
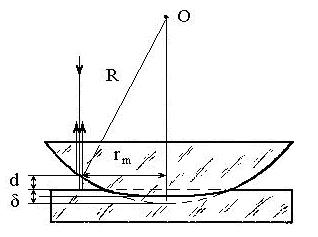
Рис.4. Учет деформации линзы и стеклянной пластинки
Учитывая (13), получим следующую формулу, для радиусов темных колец Ньютона с учетом суммарной деформации:
rm2 = Rmλ + 2Rδ (11)
Экспериментально удобнее вместо радиуса кольца Ньютона измерять его диаметр (Dm). В этом случае формула (11) будет иметь вид:
Dm2 = 4Rmλ + 8Rδ, (12)
Из (12) видно, что квадрат диаметра кольца Ньютона Dm2 пропорционален порядковому номеру кольца m. Если построить график зависимости Dm2 от m, то экспериментальные точки должны лежать на одной прямой, и тангенс угла наклона этой прямой tgα будет равен 4Rλ. Таким образом, для нахождения радиуса кривизны линзы необходимо, используя график зависимости Dm2 = f(m), найти
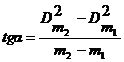, (13)
где m1, m2 номера колец,
D2m1 и D2m2 – их диаметры,
Радиус кривизны линзы затем можно рассчитать по формуле
R=tgα/4λ. (14)
В центре линзы наблюдается круглое темное пятно, соответствующее нулевой толщине воздушного зазора в области деформации. Измерив диаметр центрального темного пятна (т.е. темного кольца, номер которого m=0), из (12) можно найти величину суммарной деформации линзы и стеклянной пластинки по формуле:
δ = D02/ (8R) (15)
Лабораторная установка.
3. Описание установки (рис.7 и 8) и методика выполнения работы
Интерференционная картина наблюдается с помощью микроскопа.
Свет от источника 1, пройдя светофильтр 3, становится монохроматическим и попадает на линзу 8, помещенную на стеклянную пластинку 9.
Диаметры колец Ньютона измеряются с использованием микрометра в микроскопе ‘Эликон’ и по делениям шкалы окуляра в микроскопе МБС-9, иопределяются разницей чисел делений, приходящихся на правый и левый края измеряемого кольца.
3.1.1. Измерение диаметров колец микроскопом ‘Эликон’ (рис.7).
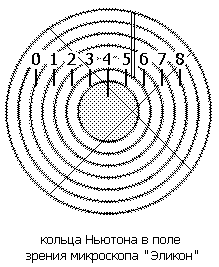
В фокальной плоскости окуляра микроскопа расположены неподвижная шкала с делениями от 0 до 8 и подвижные перекрестие и индекс в виде биштриха (двойного штриха).
При вращении микрометрического винта (барабана) перекрестие и биштрих перемещаются в поле зрения окуляра относительно неподвижной шкалы.
Барабан по окружности разделён на 100 делений. Поворот барабана на 1 деление соответствует перемещению перекрестия на 0,01 деления неподвижной шкалы. Полный отсчёт по шкале окулярного микрометра складывается из отсчета по неподвижной шкале и отсчета по барабану
На рис.7 биштрих находится между делениями "5" и "6" неподвижной шкалы, а микрометрический барабан находится, к примеру, на делении "35" (напротив неподвижного индекса).
Следовательно, полный отсчёт составляет: 500 + 35 = 535 делений. Диаметры колец определяются разницей чисел делений, приходящихся на правый и левый края измеряемого кольца.
Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.
3.1.2 Измерение диаметров колец микроскопом МБС−9 (рис.8).
В фокальной плоскости окуляра микроскопа расположены перекрестие и шкала с делениями от 0 до 18. Кольца Ньютона проецируются в центр перекрестия. Диаметры колец определяются разницей чисел делений, приходящихся на левый и правый края измеряемого кольца.
На рис.8 правый край нулевого кольца находится на делении 105, а левый−на делении 75.
Для перевода делений в мм необходимо ввести коэффициент К, учитывающий кратность увеличения микроскопа.
 |
 |
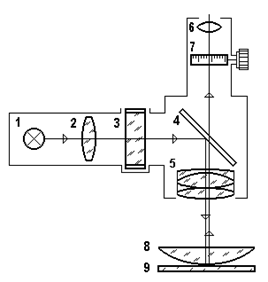Рис.7. Микроскоп “Эликон: 1−источник света, 2–конденсор,
3–светофильтр, 4–полупрозрачное зеркало, 5–объектив, 6–окуляр,
7–шкала.
Объект исследования: линза 8, лежащая на стеклянной пластине 9.
 | |||
 | |||
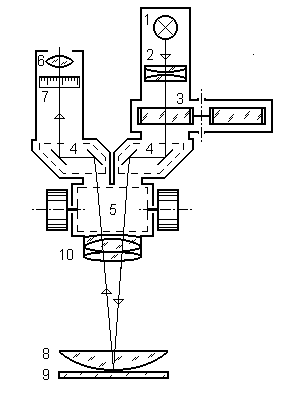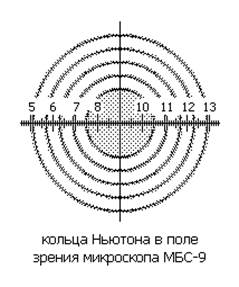Рис.8. Микроскоп МБС−9: 1−источник света, 2−конденсор,
3−светофильтр, 4−призма, 5–блок масштабирования, 6–окуляр,
7–шкала, 10−объектив.
Объект исследования: линза 8, прижатая к стеклянной пластине 9.