Лабораторная работа №2
Цель: изучить механизм вязкости; определить коэффициент вязкости жидкости методом Стокса.
Оборудование: цилиндрический стеклянный сосуд, наполненный доверху исследуемой жидкостью, пять шариков, секундомер, микрометр.
Вязкость жидкости и газа имеет большое практическое значение. Так, без знания вязкости нельзя рассчитать энергию, необходимую для транспортирования жидкости и газа по трубам (воды – в водопроводах, нефти и газа – в нефте - и газотрубопроводах), рассчитать смазку машин. Вязкость расправленного шлака и текучесть жидких металлов играет важную роль в мартеновских и доменных процессах. Знание вязкости позволяет судить о правильности и отклонениях в технологических процессах при получении полимеров и т.д. Поэтому измерение вязкости относится к числу очень важных измерений.
Цель работы – изучение механизма вязкости (или внутреннего трения). Ознакомление с одним из экспериментальных методов определения динамической вязкости жидкости – методов Стокса.
1. КРАТКОЕ ТЕОРИТИЧЕСКОЕ ВВЕДЕНИЕ.
Вязкость или внутреннее трение – свойство газообразных, жидких и твердых тел оказывать сопротивление перемещению различных слоев вещества друг относительно друга. В результате чего возникает сила, направленная в сторону, противоположную движению рассматриваемого слоя. Возникновение силы обусловлено неоднородностью скорости упорядоченного движения молекул в различных слоях (а, следовательно, и импульса), которые с течением времени за счет взаимодействия молекул выравниваются, т.е. в системе наблюдается перенос импульса от слоев с большей скоростью к слоям с меньшей скоростью движения.
|
|
Известно, что при движении жидкости или газа вдоль трубы скорости различных слоев распределены, как показано на рис.I.I.a, где стрелки соответствуют распределению векторов скорости движения по сечению трубы.
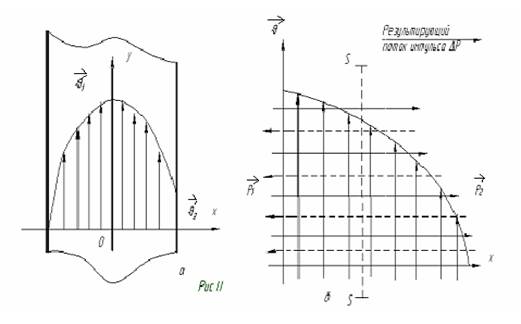
а) Распределение векторов скоростей упорядоченного движения молекул газа и жидкости по сечению трубы.
б) Направление потоков импульса между слоями вещества через площадку S. 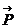 1и
1и 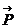 2 – потоки импульса соответственно слева направо и справа налево.
2 – потоки импульса соответственно слева направо и справа налево.
∆ 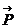 =
= 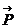 1-
1- 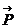 2 – результирующий поток импульса.
2 – результирующий поток импульса.
Максимальная скорость движения J1 – в центре трубы. Промежуточные слои между центром и стенкой движутся так, что каждый лежащий ближе к стенкам обладает меньшей скоростью. Благодаря смачиванию, (сцеплению за счет сил взаимодействия молекул жидкости или газа с молекулами поверхности трубы), пограничный слой прилипает к стенкам и скорости его движения U2 равна нулю.
Выделим в потоке газа или жидкости площадку S (см.рис.I.Iб). Молекулы вещества участвуют в двух видах движения – в хаотическом, тепловом и в упорядоченном движении вдоль трубы. В силу беспорядоченности движения, часть молекул будет пересекать площадку S как в направлении слева направо, так и в обратном. Количество молекул, пересекающих S в единицу времени в обоих направлениях равны, т.к. концентрация (и плотность) молекул в однородном веществе везде одинаковы. Но молекулы, переходящие слева направо переносят больший импульс 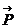 1 (скорости их выше), а молекулы, переходящие площадку S справа налево – приносят меньший
1 (скорости их выше), а молекулы, переходящие площадку S справа налево – приносят меньший 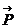 2. Поэтому, суммарный импульс вещества слева от площадки S уменшается, а справа от S увеличивается (см.рис.I.I.б). По второму закону динамики: измерение импульса в единицу времени равно действующей на слой силе
2. Поэтому, суммарный импульс вещества слева от площадки S уменшается, а справа от S увеличивается (см.рис.I.I.б). По второму закону динамики: измерение импульса в единицу времени равно действующей на слой силе 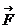 .Как впервые показал Ньютон эта сила – внутреннего трения (или вязкость), действующая на единицу поверхности слоев, пропорциональна градиенту скорости.
.Как впервые показал Ньютон эта сила – внутреннего трения (или вязкость), действующая на единицу поверхности слоев, пропорциональна градиенту скорости.
|
|
 (I.I)
(I.I)
где 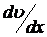 – градиент скорости, характеризующий быстроту ее изменения в направлении нормали к поверхности трудящих слоев.
– градиент скорости, характеризующий быстроту ее изменения в направлении нормали к поверхности трудящих слоев.
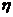 - коэффициент пропорциональности или коэффициент динамической вязкости, определяющий вязкие свойства вещества, зависящий от рода жидкости и температуры.
- коэффициент пропорциональности или коэффициент динамической вязкости, определяющий вязкие свойства вещества, зависящий от рода жидкости и температуры.
Знак ”-” показывает, что сила  является силой препятствующей движению (т.е. является силой трения).
является силой препятствующей движению (т.е. является силой трения).
Таким образом, коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади соприкосновения слоев при единичном градиенте скорости.
В системе ”СИ” η измеряется в паскаль – секундах [Па·с] (1Па·с=1Нс/м2=1кг/м·с).
Наряду с коэффициентом динамической вязкости η часто употребляется коэффициент кинематической вязкости 
(ρ плотность).
Следует помнить, что возникновение вязкости у газов обусловленно переносом импульса упорядоченного движения молекул из слоя в слой при их хаотическом тепловом движении. Внутренее трение в жидкости определяется главным образом силами молекулярного взаимодействия – силами притяжения и отталкивания. Молекулы жидкости расположены близко, поэтому они сильно связаны друг с другом (в отличие от газа). Совместные действия этих сил приводит к тому, что для каждой молекулы существует положение равновесия, около которого она колеблется в течение некоторого времени
|
|
(~10ˉ10 c). Поэтому молекулы жидкости нельзя считать свободными как в газе, а это и обусловливает большую вязкость жидкостей и ее зависимость от температуры. Перенос импульса от слоя к слою осуществляется главным образом молекулами, меняя тем самым положения равновесия, около которых они колеблются.
2. МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ.
Приборы и принадлежности: установка (вискозиметр) Стокса, электросекундомер, ареометр, масштабная линейка, набор стальных шариков, аналитические весы, разновесы, пинцет.
Определение вязкости жидкости по методу Стокса основано на измерении скорости падения стального шарика в исследуемой жидкости (рис.2.1.)
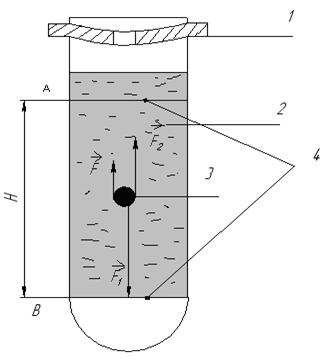
1-воронка, 2- исследуемая жидкость, 3- шарик, 4- верхняя и нижняя метки для наблюдения падения шарика.
Рассмотрим свободное падение шарика. На шарик в жидкости действуют силы (см.рис.2.1.)
а) Сила тяжести
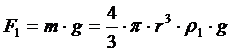 (2.1)
(2.1)
Где г – радиус шарика
p1 – плотность вещества шарика,
g – ускорение свободного падения,
б) Выталкивающая сила Архимеда

Где ρ2 – плотность жидкости.
в) Сила внутреннего трения (сопротивления движения).
Как показал Стокс, сила действующая на шарик малого размера прямо пропорциональна скорости его падения J, его радиусу к и зависит от вязкости (внутреннего трения) жидкости:
 (2.3.)
(2.3.)
Следует подчеркнуть, что здесь роль играет нет трение шарика о жидкость, а трение отдельных слоев жидкости друг о друге, так как при соприкосновении твердого тела с жидкостью к поверхности твердого тела с жидкостью к поверхности тела тот час прилипают молекулы жидкости за счет сил межмолекулярного взаимодействия, образуя слой, движущеийся вместе с шариком. При своем движении он увлекает соседние слои жидкости, которые на некоторый период приходят в плавное безвихревое (ламинарное) движение, так как скорость и размеры шарика малы.
Вначале скорость падения шарика будет возрастать, но возростает и сила внутреннего трения 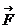 (см.рис.2.3.) и через некоторое время наступит состояние, когда равнодействующая всех сил, действующих на шарик, станет равной нулю:
(см.рис.2.3.) и через некоторое время наступит состояние, когда равнодействующая всех сил, действующих на шарик, станет равной нулю:
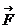 1+
1+ 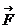 2+
2+ 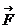 =0 или F1=F2+F
=0 или F1=F2+F
И шарик равномерно будет падать с постоянной скоростью J.
Подставляя в выражение (2.4) значения F1, F2, и F, получим для коэффициента вязкости:
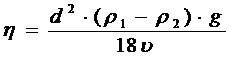 (2.5)
(2.5)
Для определения скорости падения шарика применяется установка, представляющая собой высокий стеклянный цилиндрический сосуд (см.рис.2.1.), наполненный жидкостью. Сверху сосуд закрыт воронкой 1 с центральным отверстием для опускания шариков. На сосуде имеются метки 4 – А и В (см.рис.2.1.). Метка А распологается на такой высоте, где движение шарика уже имеет постоянную скорость (см.п.4)
Зная расстояние между метками А и В и время падения t, в течение которого шарик проходит это расстояние Н находим:
J =H/t (2.6)
Подставляя значение скорости и выражение (2.5) получаем расчетную формулу для вязкости жидкости
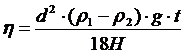 (2.7)
(2.7)
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ .
Микрометром измеряют диаметр каждого шарика и заносят в таблицу 3.1.
Таблица 3.1.
| № | di мм | (di-<d>) мм | (di-<d>)2 мм2 |
| <d> | Σ (di-<d>)2= i |
Среднеквадратичное отклонение среднего арифметического диаметра
S<d>=…………… мм
Систематическая ошибка измерения диаметра
δd =…………….. мм
Определяем на аналитических весах массу всех пяти шариков в соответствии с правилами взвешивания (см. приложение №….), затем находим массу одного шарика М.
Систематическую погрешность при определении массы принять равной цене деления весов
δМ=………….. г.
Рассчитываем плотность материала шариков по формуле
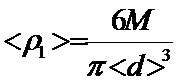 , (3.1)
, (3.1)
где М – масса одного шарика.
Систематическую погрешность определения <ρ> оцениваем по выражению:
δρ= 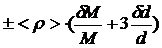 (3.2)
(3.2)
С помощью масштабной линейки определяем высоту падения шарика Н (расстояние между метками на установке Стокса рис.2.1).
За систематическую погрешность при определении высоты следует принять цену деления масштабной линейки, т.к. отсчет делается и по верхней и по нижней метке.
δН=………. мм
Измеряем электросекундомером время падения каждого шарика.
Результаты измерений заносим в таблицу № 3.2.
Таблица 3.2.
| № | ti, с | ti - <t>, c | (ti-<t>)2, с2 |
| <t> | Σ (ti-<t>)2= i |
Среднеквадратичное отклонение среднего арифметического времени падения:
S<t>=……….. с
Систематическая ошибка при измерении времени падения принимается равной половине цены деления электросекундомера:
δt=………. с
С помощью ареометра или денсиметра определяем плотность следуемой жидкости ρ2. За систематическую ошибку измерений ρ2 принимают половину цены деления прибора
δρ2=………… кг/м3
По уравнению (2.7) рассчитываем вязкость жидкости.
Находим систематическую погрешность при определении вязкости
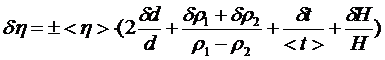 (3.3)
(3.3)
случайная погрешность при доверительной вероятности 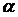 =0,95
=0,95
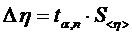 (3.4)
(3.4)
где
 (3.5)
(3.5)
Среднеквадратичное отклонение а 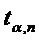 - коэффициент Стьюдента.
- коэффициент Стьюдента.
Вычислить величину и по следующим критериям делать оценку систематической и случайной погрешностей.
Окончательный результат записать в виде
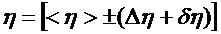
При этом следует указать комнатную температуру и атмосферное давление, т.к. вязкость жидкости очень сильно зависит от колебания температуры.
4. ВОПРОСЫК ДОПУСКУ
1. Что такое вязкость?
2. Что характеризует коэффициент вязкости?
3. В каких единицах измеряется коэффициент вязкости?
4. Что такое градиент скорости?
5. Объяснить механизм возникновения вязкого трения и указать факторы его определяющие.
6. Какое течение жидкости называется ламинарным? Турбулентным?
7. Что характеризует число Рейнольдса?
8. Что такое предельная скорость?
9. Существует ли предельная скорость при сухом трении?
10. Чему примерно равна предельная скорость человека при падении в воздухе?
11. Откуда следует необходимость существования предельной скорости движения при наличии жидкого трения?
12. Каково практическое значение знания вязкости жидкости?
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чём сущность метода Стокса?
2. За счёт чего возникают систематические и случайные ошибки в данной работе?
3. Почему в сосуде другого диаметра результат экспериментальной оценки получают другим?
4. Можно ли для оценки среднего значения коэффициента вязкости в расчетную формулу подставлять усредненные результаты прямых измерений?
5. *Описать различия в динамике движения парашютиста при его выпрыгивании с аэростата и из быстро летящего самолёта.
6. *В сосуде с глицерином при t = 20°C падает стальной шарик плотностью p1 = 7,8 ∙ 103 кг/м3. Определить, какое максимальное значение должен иметь диаметр шарика, чтобы движение слоев жидкости, вызванное его движением, было ламинарным. Считать, что движение жидкости является стационарным (v=const). Принять плотность глицерина р2 =1,26103 кг/м3 и коэффициент внутреннего трения 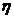 = 1,4 Нс/м2.
= 1,4 Нс/м2.
7. Стальной шарик диаметром d=3,0 мм опускается с нулевой начальной скоростью в прованском масле, вязкость которого 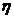 =90 мПа∙с. Через сколько времени после начала движения скорость шарика будет отличаться от установившегося значения на n=0,1%?
=90 мПа∙с. Через сколько времени после начала движения скорость шарика будет отличаться от установившегося значения на n=0,1%?