Для определения поперечных колебаний смоделируем тягу струной.
Волнами называются возмущения, распространяющиеся в среде или в вакууме и несущие с собой энергию. При этом перенос энергии происходит без переноса вещества, т.е. частицы среды, в которой распространяется волна, не вовлекаются в поступательное движение, а совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные и поперечные волны. В поперечной волне частицы совершают колебания в направлениях, перпендикулярных направлению распространения колебаний, а в продольных волнах – вдоль направления распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. К ним, в частности, относятся поперечные колебания струны.
Составим уравнение колебаний струны, натянутой между двумя точками её закрепления, при условии, что амплитуда отклонений струны от положения равновесия настолько мала, что длину струны( ) можно считать постоянной, а натяжение
) можно считать постоянной, а натяжение  струны – неизменным по всей длине струны и не зависящим от времени.
струны – неизменным по всей длине струны и не зависящим от времени.
Рассмотрим отрезок  (рис. 2) колеблющейся однородной струны, точки закрепления которой находятся на оси
(рис. 2) колеблющейся однородной струны, точки закрепления которой находятся на оси  . Пусть в некоторый момент времени на струну было оказано воздействие, приведшее к смещению отрезка
. Пусть в некоторый момент времени на струну было оказано воздействие, приведшее к смещению отрезка  из положения равновесия (вдоль оси
из положения равновесия (вдоль оси  ) в направлении оси
) в направлении оси  .
.
Смещения струны вдоль оси 
 |
Так как в исходном положении струна была натянута, то к концам отрезка будут приложены равные силы натяжения  , образующие с направлением
, образующие с направлением  углы
углы  . В интересах наглядности изображения на (рис. 2) использован укрупненный масштаб при изображении смещения струны вдоль оси
. В интересах наглядности изображения на (рис. 2) использован укрупненный масштаб при изображении смещения струны вдоль оси  .Поэтому при дальнейших расчетах следует иметь ввиду, во-первых, что на (рис. 2) изображен только некоторый произвольно выбранный отрезок струны и,
.Поэтому при дальнейших расчетах следует иметь ввиду, во-первых, что на (рис. 2) изображен только некоторый произвольно выбранный отрезок струны и,
во-вторых, что смещение вдоль оси  существенно меньше длины струны, а углы настолько малы, что с большой точностью соблюдаются приближенные соотношения:
существенно меньше длины струны, а углы настолько малы, что с большой точностью соблюдаются приближенные соотношения:
 ,
,  . (3)
. (3)
Проекции сил 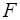 на ось
на ось  , с учетом соотношений (3), соответственно равны:
, с учетом соотношений (3), соответственно равны:

(4)

Алгебраическая сумма проекций сил, описываемых соотношениями (4), является силой, возвращающей отрезок  в положение равновесия. При этом рассматриваемая часть струны (рис. 2) будет последовательно принимать положения 1,2,3 и т.д., пока колебания не прекратятся и струна не займет устойчивое положение вдоль оси
в положение равновесия. При этом рассматриваемая часть струны (рис. 2) будет последовательно принимать положения 1,2,3 и т.д., пока колебания не прекратятся и струна не займет устойчивое положение вдоль оси  .
.
На основании второго закона Ньютона результирующая сила, действующая на отрезок  , равна произведению его массы на ускорение
, равна произведению его массы на ускорение 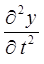 , сообщаемое отрезку
, сообщаемое отрезку  возвращающей силой:
возвращающей силой:
 . (5)
. (5)
Разделив правую и левую части соотношения (5) на 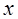 , при значениях
, при значениях  получим:
получим:
 , или
, или
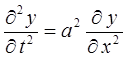 , (6)
, (6)
где  ;
;  – линейная плотность струны
– линейная плотность струны
Соотношения типа (6) называются волновыми уравнениями, решение которых можно искать в следующем виде:
 . (7)
. (7)
Подставляя соотношение (7) в формулу (6), получим:
 . (8)
. (8)
Уравнение (8) записано в обыкновенных производных, т.к.  и
и 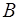 зависят только от
зависят только от 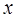 и
и  соответственно. Так как
соответственно. Так как 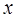 и
и  – независимые переменные, то равенство (8) может соблюдаться во всем диапазоне их измерений, если обе части соотношения (8) являются некоторой постоянной величиной, которую обозначим
– независимые переменные, то равенство (8) может соблюдаться во всем диапазоне их измерений, если обе части соотношения (8) являются некоторой постоянной величиной, которую обозначим  . После проведения очевидных преобразований соотношение (8) может быть записано в следующей форме:
. После проведения очевидных преобразований соотношение (8) может быть записано в следующей форме:
 . (9)
. (9)
Соотношение (7) позволяет составить следующие уравнения:
 ,
,
(10)
 .
.
Решения дифференциальных уравнений (10) имеют вид:
 ,
,  .
.
Следовательно, решение (7) волнового уравнения (6) имеет вид:
 , (11)
, (11)
где  – амплитудные значения колебаний, формирующихся в точке с координатой
– амплитудные значения колебаний, формирующихся в точке с координатой 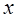 в результате сложения волн, распространяющихся вдоль струны за счет действия возмущающей силы и отраженных от точек закрепления оконечных участков струны. Возникающий в результате колебательный процесс (11) называется стоячей волной. Точки, в которых
в результате сложения волн, распространяющихся вдоль струны за счет действия возмущающей силы и отраженных от точек закрепления оконечных участков струны. Возникающий в результате колебательный процесс (11) называется стоячей волной. Точки, в которых  , называются узлами, а точки, в которых амплитуда максимальна
, называются узлами, а точки, в которых амплитуда максимальна  – пучностями стоячей волны. Следует иметь в виду, что и пучность, и узел представляют собой не точки, а плоскости, удовлетворяющие указанным условиям. Расстояние между соседними пучностями (также как и между соседними узлами) равно половине длины волны
– пучностями стоячей волны. Следует иметь в виду, что и пучность, и узел представляют собой не точки, а плоскости, удовлетворяющие указанным условиям. Расстояние между соседними пучностями (также как и между соседними узлами) равно половине длины волны  . Соседние узел и пучность сдвинуты на
. Соседние узел и пучность сдвинуты на  .
.
Для нахождения неопределенной постоянной  в уравнении (11) воспользуемся очевидными граничными условиями, обусловленными тем, что в точках закрепления струны амплитуда равна нулю:
в уравнении (11) воспользуемся очевидными граничными условиями, обусловленными тем, что в точках закрепления струны амплитуда равна нулю:
 . (12)
. (12)
Следовательно,
 или
или  , (13)
, (13)
где  =1,2,3... – определяет число пучностей.
=1,2,3... – определяет число пучностей.
Введем для формулы (11) следующие обозначения:
 , (14)
, (14)
где  ;
;
 – циклическая частота колебаний;
– циклическая частота колебаний;
 – частота колебаний.
– частота колебаний.
С учётом соотношений (6), (13) и (14) имеем:
 . (15)
. (15)
При установившейся стоячей волне вся длина струны 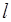 содержит целое число
содержит целое число  полуволн, т.к. в конечных точках струны согласно (12)
полуволн, т.к. в конечных точках струны согласно (12)  . Таким образом,
. Таким образом,  и, соответственно:
и, соответственно:  . (16)
. (16)
Так как скорость распространения колебаний:
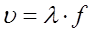 , (17)
, (17)
то с учетом формул (15) и (16) имеем:
 . (18)
. (18)
В равенстве (18) можно перейти от линейной к объемной плоскости струны 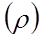 :
:
 , (19)
, (19)
где 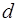 – диаметр струны.
– диаметр струны.
При этом соотношение (15) можно записать в виде:
 . (20)
. (20)
Частота, соответствующая  =1, называется основной
=1, называется основной  , а частоты, соответствующие
, а частоты, соответствующие  >1 – собственными или нормальными частотами. Их также называют гармониками. В общем случае колебание струны представляет собой наложение гармоник.
>1 – собственными или нормальными частотами. Их также называют гармониками. В общем случае колебание струны представляет собой наложение гармоник.
Экспериментальная часть
Разработанная установка представляет собой натянутую струну колеблющуюся, в результате воздействия на нее потоком воздуха.
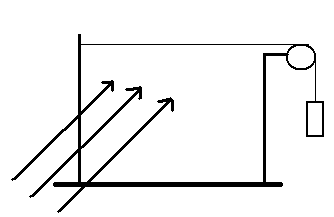
2.1 Описание установки



Рис.3 Экспериментальная установка
1.Платформа на ножках;
2.Стойка(1);
3.Стойка(2);
4.Груз;
5.Блок(рис.4);
6.Болт крепления струны(рис.5)
7.Струна


| |||
| |||