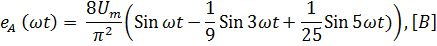Параметры элементов схемы для первой гармоники.

Задание

Питание нагрузки осуществляется от симметричного несинусоидального трехфазного источника. Задана схема цепи, ее параметры, форма кривой ЭДС e_A фазы А источника, номер рубильника, включение или отключение которого делает цепь несимметричной. Частота f = 50 Гц.

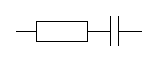
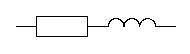
Типы сопротивлений схемы и № рубильника создающего несимметрию

№	№ рубильника	Z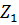
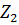
	S1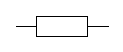
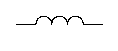
	S2
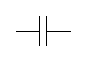
	S3
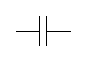
	S4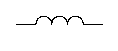
	S1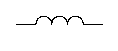
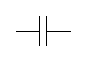
	S2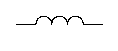
	S3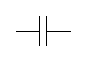
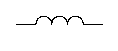
	S4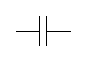
	S1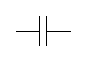
	S2
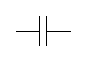
	S3
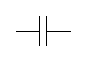
	S4
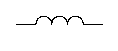
	S1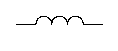
	S2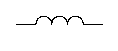
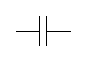
	S3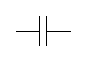

 

Параметры элементов схемы для первой гармоники.

№ вар		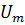r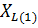
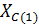
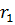
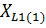
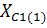
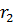
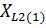
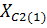
В	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом	Ом

 

Содержание работы:

- найти вид разложения функции e_A (ωt) в ряд Фурье;

- для симметричного режима определить мгновенные значения токов и напряжений во всех ветвях схемы;

- определить показания амперметра электродинамической системы и построить график изменения измеряемого тока в зависимости от времени за один период;

- определить мощность, измеряемую ваттметрами;

- построить векторные диаграммы токов и напряжений для всех гармоник.

Примечание:

- при расчете учесть первые 3 гармоники;

- векторная диаграмма токов каждой из гармоник должна быть наложена на топографическую диаграмму напряжений и изображена другим цветом.

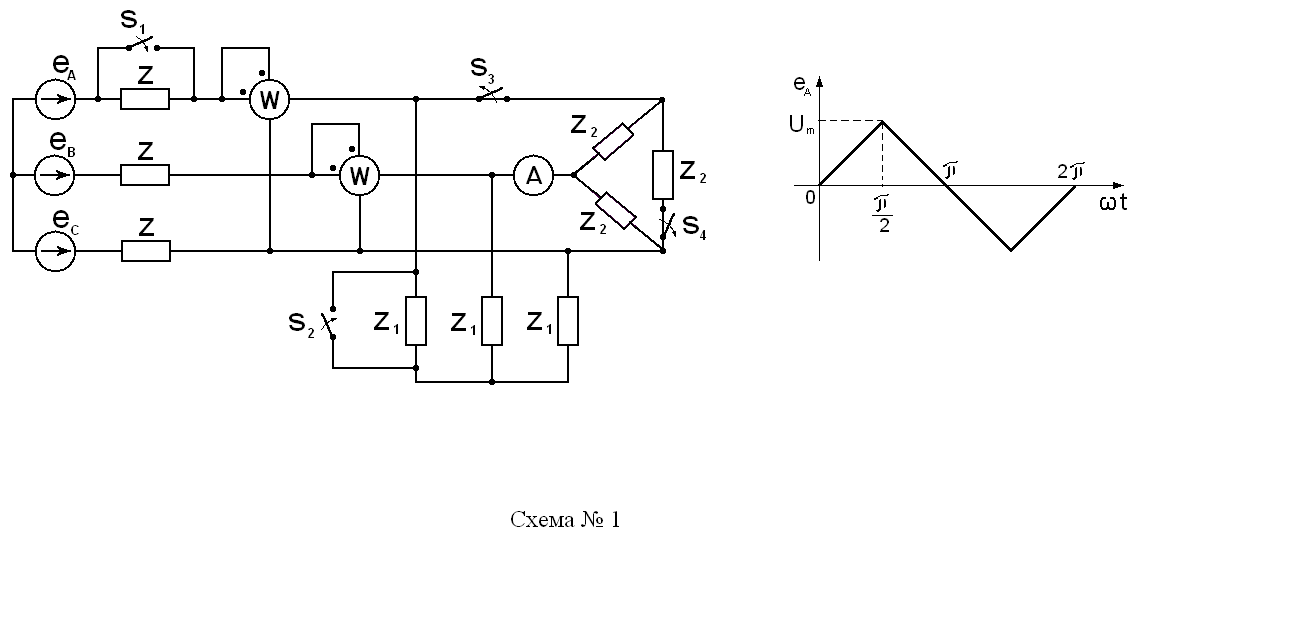
Методику выполнения задания рассмотрим на примере аналогичной цепи (схема 1).

Пусть заданы следующие параметры схемы:

U_m, r₁ , r₂ , X_L(1), X_{C1 (1)}. Импеданс Z состоит из X_L, импеданс Z₁ состоит из r₁, X_C1, импеданс Z₂ состоит из r₂. Форма кривой ЭДС е_А – треугольная.

Трехфазная нагрузка Z1 соединена звездой, Z2 - треугольником.

Решение:

1. Разложим заданную функцию входного напряжения e_A (ωt) в ряд Фурье, ограничившись первыми тремя ненулевыми гармониками. Поскольку функция нечетная, то ряд Фурье будет содержать только синусные составляющие см.(*)

e_A (ωt) = 8 U_m / п² (Sin ωt – Sin ( 3 ωt + 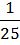Sin ( 5 ωt))

вычисляем амплитуды гармоник 1, 3, 5:

e₁ = 8 U_m / п²= 8·180 / 3,14² = 145,9

e₃ = - 8 U_m / 9 п² = -145,9 / 9 = -16,2

e₅ = 8 U_m / 25 п² = 145,9 / 25 = 5,8

тогда

e_A1 = 145,9 Sin ωt

e_A3 = -16,2 Sin 3 ωt

e_A5 = 5,8 Sin 5 ωt

e_B1 = 145,9 Sin (ωt – 120°)

e_B3 = -16,2 Sin (3 ωt – 360°)

e_B5 = 5,8 Sin (5 ωt – 600°)

e_C1 = 145,9 Sin (ωt + 120°)

e_C3 = -16,2 Sin (3 ωt + 360°)

e_C5 = 5,8 Sin (5 ωt + 600°)

 

Полное разложение в ряд Фурье

для ЭДС каждой из ветвей:

e_A (ωt) = 145,9 Sin ωt – 16,2 Sin 3 ωt + 5,8 Sin 5 ωt

e_B (ωt) = 145,9 Sin (ωt – 120°) -16,2 Sin (3 ωt – 360°) + 5,8 Sin (5 ωt – 600°)

e_C (ωt) = 145,9 Sin (ωt + 120°) -16,2 Sin (3 ωt + 360°) + 5,8 Sin (5 ωt + 600°)

А. Исследуем цепь в симметричном режиме, в котором все рубильники находятся в исходном положении.

А.1. Разложение функции входного напряжения в ряд Фурье приведено выше.

А.2. Определим выражение для мгновенных значений токов и напряжений во всех ветвях схемы. Убираем из схемы рубильник и измерительные приборы.

А.2.1. Определим вначале комплексы действующих величин ЭДС, токов и напряжений во всех ветвях для первых трех ненулевых гармоник.

А.2.1.1. 1 – я гармоника.

Переходим от мгновенных значений ЭДС к комплексам их действующих значений:

e_{A (1)} E_{A (1)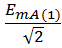} = = 103,1687 e ^j0°

e_{B (1)} E_{B (1)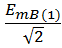} = e ^{–j120 °} = 103,16877 e ^-j120°

e_{C (1)} E_{C (1)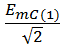} = e ^j120 = 103,1687 e ^j120°

Определим комплексы полных сопротивлений фаз приемников. Для этого записываем выражения для комплексных сопротивлений Z, Z1, Z2:

Z = 0 + j 8 = 8 e ^j90° , Ом

Z₁ = 15 – j 15 = 21.2132 e ^–j45°, Ом

Z₂ = 10 + j 0 = 10 e ^j0°, Ом

Заменяем треугольник из одинаковых сопротивлений Z₂ эквивалентной звездой из сопротивлений Z'₂ (с учетом ее симметричности):

 

Z'₂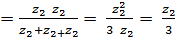

 

Z'₂ = 3.3333 + j0 = 3.3333 e ^j0° Ом

 

Очевидно, что потенциалы точек А₁ и А₂, В₁ и В₂, С₁ и С₂ соответственно одинаковы. Кроме того, из соображений симметрии цепи следует, что потенциалы точек О₁ и О₂ также одинаковы, т.е. их можно соединить. Поэтому можно считать, что сопротивления Z'₁ и Z'₂ соединены параллельно, тогда

 

Z₁₂ = Z'₁ Z'₂ / (Z'₁ + Z'₂) = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

(см.рис.4)

 

Тогда полное сопротивление одной ветви симметричной цепи

 

Z_общ = 0 + j8 + 2.9703 – j0.2970 = 2.9703 + j7.7030 = 8.2558e ^j68.91° Ом

 

Вычисляем токи неразветвленной части цепи

I_{A (1)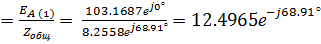} А

 

I_{В (1)} А

 

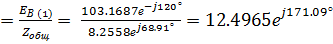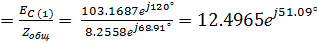I_{С (1)} А

 

Проверяем равенство нулю векторной суммы всех токов (истинность первого уравнения Кирхгофа для узла 0):

 

I_A + I_B + I_C = 4.4960 – j11.6597 – 12.3456 + j1.9362 + 7.8496 + j9.7235 = 0 + j0 = 0

 

Итак, баланс выполняется, т.е. токи найдены правильно.

Теперь вычислим токи через сопротивления Z₁ и Z₂ в каждой ветви. Вначале вычислим падения напряжения на соответствующих парах параллельных сопротивлениях.

 

U_A1ON = Z₁₂ I_A = 2.9851e ^–j5.71° 12.4965e ^–j68.91° = 37.3034e ^–j74.62° B

U_B1ON = Z₁₂ I_B = 2.9851e ^–j5.71° 12.4965e ^j171.09° = 37.3034e ^j165.38° B

U_C1ON = Z₁₂ I_C = 2.9851e ^–j5.71° 12.4965e ^j51.09° = 37.3034e ^j45.38° B

U_A1B1 = ϕ_A1 – ϕ_B1 = ϕ_A1 - ϕ_ON + ϕ_ON - ϕ_B1 = U_A1ON – U_B1ON

U_B1C1 = ϕ_B1 – ϕ_C1 = ϕ_B1 - ϕ_ON + ϕ_ON - ϕ_C1 = U_B1ON – U_C1ON

U_A1B1 = ϕ_C1 – ϕ_A1 = ϕ_C1 - ϕ_ON + ϕ_ON - ϕ_A1 = U_C1ON – U_A1ON

U_A1B1 = 9.8912 – j35.9682 – (-36.0950 + j9.4180) = 45.9862 – j45.3862 = 64.6114e ^–j44.62° B

U_B1C1 = -36.0950 + j9.4180 – (26.2037 + j26.5501) = -62.2987 – j17.1321 = 64.6114e ^–j164.62° B

U_C1A1 = 26.2037 + j26.5501 – (9.8912 – j35.9682) = 16.3125 + j62.5183 = 64.6114e ^j75.38° B

Тогда токи соответствующих разветвлений

I_A1O1 = U_A1ON / Z₁ = 37.3034e ^–j74.62° / 21.2132e ^–j45° = 1.7585e ^–j29.62° A

I_B1O1 = U_B1ON / Z₁ = 37.3034e ^j165.38° / 21.2132e ^–j45° = 1.7585e ^–j149.62° A

I_C1O1 = U_C1ON / Z₁ = 37.3034e ^j45.38° / 21.2132e ^–j45° = 1.7585e ^j90.38° A

I_A1B1 = U_A1B1 / Z₂ = 64.6114e ^–j44.62° / 10e ^j0° = 6.4611e ^–j44.62° A

I_B1C1 = U_B1C1 / Z₂ = 64.6114e ^–j164.62° / 10e ^j0° = 6.4611e ^–j164.62° A

I_C1A1 = U_C1A1 / Z₂ = 64.6114e ^j75.38° / 10e ^j0° = 6.4611e ^j75.38° A

Вычислим падения напряжения на сопротивлениях в неразветвленной части схемы:

U_AA1 = Z I_A = 8e ^j90° 12.4965e ^-j68.91° = 99.9719e ^j21.09° B

U_BB1 = Z I_B = 8e ^j90° 12.4965e ^j171.09° = 99.9719e ^–j98.91° B

U_CC1 = Z I_C = 8e ^j90° 12.4965e ^j51.09° = 99.9719e ^j141.09° B

А.2.1.3. Для третьей гармоники токи заведомо равны нулю. Действительно, при отсутствии нулевого провода в трехфазной системе сумма фазных токов в любом случае равна нулю, а для гармоник, кратных трем, токи для всех фаз синфазны. Тогда равенство нулю суммы фазных токов может реализоваться только в случае равенства нулю токов каждой из фаз в отдельности.

А.2.1.5. 5 – я гармоника.

Переходим от мгновенных значений ЭДС к комплексам их действующих значений:

e_{A (5)} E_{A (5)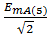} = = 4.1267e ^j0°

e_{B (5)} E_{B (5)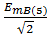} = e ^–j600° = 4.1267e ^–j600°

e_{C (5)} E_{C (5)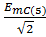} = e ^j600 = 4.1267e ^j600°

Определим комплексы полных сопротивлений фаз приемников. Для этого записываем выражения для комплексных сопротивлений Z, Z1, Z2:

 

Z₁ = 15 – j3 = 15.2971e ^–j11.31° Ом

Z₂ = 10 + j0 = 10e ^j0° Ом

Заменяем треугольник из одинаковых сопротивлений эквивалентной звездой из сопротивлений (с учетом ее симметричности):

Z'₂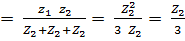

Z'₂ = 3.3333 + j0 = 3.3333e ^j0° Ом

Получаем в итоге схему рис. 2

Очевидно, что потенциалы точек А₁ и А₂, В₁ и В₂, С₁ и С₂ соответственно одинаковы. Кроме того, из соображений симметрии цепи следует, что потенциалы точек О₁ и О₂ также одинаковы, т.е. их можно соединить. Поэтому можно считать, что сопротивления Z'₁ и Z'₂ соединены параллельно, тогда

Z₁₂ = Z'₁ Z'₂ / (Z'₁ + Z'₂) = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом (см.рис.4)

Тогда полное сопротивление одной ветви симметрично цепи

Z_общ = 0 + j40 + 2.7431 – j0.0966 = 2.7431 + j39.9036 = 39.9976e ^j86.07° Ом

Вычисляем токи неразветвленной части цепи

I_A(5) 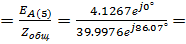0.1032e ^–j86.07° A

I_B(5) 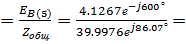0.1032e ^j33.93° A

I_C(5) 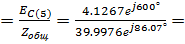0.1032e ^j153.93° A

Проверяем равенство нулю векторной суммы всех токов (истинность первого уравнения Кирхгофа для узла 0):

I_A + I_B + I_C = 0.0071 – j0.1029 + 0.0856 + j0.0576 – 0.0927 + j0.453 = 0 + j0 = 0

Итак, баланс выполняется, т.е. токи найдены правильно.

Теперь вычислим токи через сопротивления Z₁, Z₂ в каждой ветви. Вначале вычислим падения напряжения на соответствующих парах параллельных сопротивлениях

U_A1ON = Z₁₂ I_A = 2.7448e ^–j2.02° 0.1032e ^–j86.07° = 0.2832e ^–j88.08° B

U_B1ON = Z₁₂ I_B = 2.7448e ^–j2.02° 0.1032e ^j33.93° = 0.2832e ^j31.92° B

U_C1ON = Z₁₂ I_C = 2.7448e ^–j2.02° 0.1032e ^j153.9° = 0.2832e ^j151.92° B

U_A1B1 = ϕ_A1 – ϕ_B1 = ϕ_A1 - ϕ_ON + ϕ_ON - ϕ_B1 = U_A1ON – U_B1ON

U_B1C1 = ϕ_B1 – ϕ_C1 = ϕ_B1 - ϕ_ON + ϕ_ON - ϕ_C1 = U_B1ON – U_C1ON

U_A1B1 = ϕ_C1 – ϕ_A1 = ϕ_C1 - ϕ_ON + ϕ_ON - ϕ_A1 = U_C1ON – U_A1ON

U_A1B1 = 0.0095 – j0.2830 – (0.2404 + j0.1497) = - 0.2309 – j0.4327 = 0.4905e ^–j118.08° B

U_B1C1 = 0.2404 – j1497– (- 0.2498 + j0.1333) = 0.4902 + j0.0164 = 0.4905e ^j1.92° B

U_C1A1 = - 0.2498 – j0.1333 – (0.0095 + j0.2830) = - 0.2593 + j0.4164 = 0.4905e ^j121.92° B

Тогда токи соответствующих разветвлений

I_A1O1 = U_A1ON / Z₁ = 0.2832e ^–j88.08° / 15.2971e ^–j11.31° = 0.0185e ^–j76.77° A

I_B1O1 = U_B1ON / Z₁ = 0.2832e ^j31.92° / 15.2971e ^–j11.31° = 0.0185e ^j43.23° A

I_C1O1 = U_C1ON / Z₁ = 0.2832e ^j151.92° / 15.2971e ^–j11.31° = 0.0185e ^j163.23° A

I_A2B2 = U_A1B1 / Z₂ = 0.4905e ^–j118.08° / 10e ^j0.00° = 0.0491e ^–j118.08° A

I_B2C2 = U_B1C1 / Z₂ = 0.4905e ^j1.92° / 10e ^j0.00° = 0.0491e ^j1.92° A

I_C2A2 = U_C1A1 / Z₂ = 0.4905e ^j121.92° / 10e ^j0.00° = 0.0491e ^j121.92° A

Вычислим падения напряжения на сопротивлениях в неразветвленной части схемы:

U_AA1 = Z I_A = 40e ^j90.00° 0.1032e ^–j86.07° = 4.1207e ^j3.93° B

U_BB1 = Z I_B = 40e ^j90.00° 0.1032e ^j33.93° = 4.1207e ^j123.93° B

U_CC1 = Z I_C = 40e ^j90.00° 0.1032e ^j153.93° = 4.1207e ^–j116.07° B

i_A(t) = 17.67 Sin (ωt – 68.91°) + 0.15 Sin (5ωt – 86.07°)

i_B(t) = 17.67 Sin (ωt + 171.09°) + 0.15 Sin (5ωt + 33.93°)

i_C(t) = 17.67 Sin (ωt + 51.09°) + 0.15 Sin (5ωt + 153.93°)

i_AZ1(t) = 2.49 Sin (ωt – 29.62°) + 0.03 Sin (5ωt – 76.77°)

i_BZ1(t) = 2.49 Sin (ωt – 149.62°) + 0.03 Sin (5ωt + 43.23°)

i_CZ1(t) = 2.49 Sin (ωt + 90.38°) + 0.03 Sin (5ωt + 163.23°)

i_ABZ2(t) = 9.14 Sin (ωt – 44.62°) + 0.07 Sin (5ωt – 118.08°)

i_BCZ2(t) = 9.14 Sin (ωt – 164.62°) + 0.07 Sin (5ωt + 1.92°)

i_CAZ2(t) = 9.14 Sin (ωt + 75.38°) + 0.07 Sin (5ωt + 121.92°)

U_AZ(t) = 141.38 Sin (ωt + 21.09°) + 5.84 Sin (5ωt + 3.93°)

U_BZ(t) = 141.38 Sin (ωt – 98.91°) + 5.84 Sin (5ωt + 123.93°)

U_CZ(t) = 141.38 Sin (ωt + 141.09°) + 5.84 Sin (5ωt – 116.07°)

U_AZ1(t) = 52.75 Sin (ωt – 74.62°) + 0.40 Sin (5ωt – 88.08°)

U_BZ1(t) = 52.75 Sin (ωt + 165.38°) + 0.40 Sin (5ωt + 31.92°)

U_CZ1(t) = 52.75 Sin (ωt + 45.38°) + 0.40 Sin (5ωt + 151.92°)

U_ABZ2(t) = 91.37 Sin (ωt – 44.62°) + 0.69 Sin (5ωt – 118.08°)

U_BCZ2(t) = 91.37 Sin (ωt – 164.62°) + 0.69 Sin (5ωt + 1.92°)

U_CAZ2(t) = 91.37 Sin (ωt + 75.38°) + 0.69 Sin (5ωt + 121.92°)

А.3. Определяем показания амперметра электродинамической системы по формуле

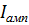
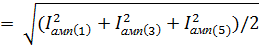
Запишем комплексы амплитуд отдельных гармоник:

I_{амперметр (1)} = 15.8265e ^j165.38° A

I_{амперметр (3)} = 0e ^j0° A

I_{амперметр (5)} = 0.1201e ^j31.92° A

тогда

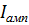
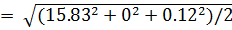= 11.19 А

Запишем выражение для тока в ветви с амперметром:

i_амп (t) = 15.826Sin (ωt + 165.38°) + 0.120Sin (5ωt + 31.92°) (см.рис.5)

А.4. Определяем мощность измеряемую ваттметрами для ваттметра W1 в 1 – й ветви по формуле

P = Re (S_W1),

S_W1 = Ʃ_1,3,5 U_W1 I_W1* = U_W1(1) I*_{W1 (1)} + U_W1(3) I*_W1(3) + U_W1(5) I*_W1(5)

для ваттметра W2 в 2 – й ветви по формуле

P = Re (S_W2),

S_W2 = Ʃ_1,3,5 U_W2 I_W2* = U_W2(1) I*_{W2 (1)} + U_W2(3) I*_W2(3) + U_W2(5) I*_W2(5)

где суммирование идет по всем гармоникам. Учитывая, что токи третьей гармоники равны нулю, получим

U_{W1 (1)} = 64.61e ^–j104.62° B

I_{W1 (1)} = 12.4965e ^–j68.91° A

U_{W1 (1)} I*_W1(1) = 807.42e ^–j35.71° B A

U_{W1 (5)} = 0.49e ^–j58.08° B

I_{W1 (5)} = 0.1032e ^–j86.07° A

U_{W1 (5)} I*_W1(5) = 0.05e ^j27.98° B A

S_W1 = 807.4382e ^–j35.71° = 655.6466 – j471.2579

P_W1 = 655.65 Вт

U_W2(1) = 64.61e ^–j164.62° B

I_W2(1) = 12.4965e ^j171.09° A

U_W2(1) I*_W2(1) = 807.42e ^j24.29° B A

U_W2(5) = 0.49e ^j1.92° B

I_W2(5) = 0.1032e ^j33.93° A

U_W2(5) I*_W2(5) = 0.05e ^–j32.02° B A

S_W2 = 807.4438e ^j24.29° = 735.9857 + j332.1003

P_W2 = 735.99 Вт

А.5. Строим векторные диаграммы для всех гармоник.

Несимметричная схема получается из исходной путем замыкания ключа S₁, вследствие чего закорачивается сопротивление Z в ветви А.

После этого цепь приобретает вид, изображенный на рис.8. Из схемы убираем рубильник и измерительные приборы.

В этом случае сопротивление части схемы, находящейся правее точек А₁, В₁, С₁, вычисляем также, как было описано выше, а затем учитываем, что сопротивление Z в ветви А закорочено, т.е. Z = 0. Точнее говоря, преобразуем правую часть ветви в эквивалентную звезду Z₁₂, сопротивления ветвей которой для каждой из гармоник были рассчитаны выше, а затем вычислим сопротивления ветвей в целом по формулам

Z_Aобщ = Z_A1

Z_Bобщ = Z + Z_B1

Z_Cобщ = Z + Z_C1

где Z_A1 = Z_B1 = Z_C1 = Z₁₂

Далее вычисляем проводимости ветвей

Y_A = 1 / Z_Aобщ

Y_В = 1 / Z_Вобщ

Y_С = 1 / Z_Собщ

и смещение точки О₁ относительно О:

U_O1O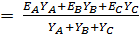

Токи отдельных ветвей по формулам

I_A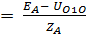

I_A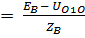

I_B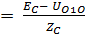

В.1. Разложение функции входного напряжения в ряд Фурье приведено выше.

В.2. Определим выражения для мгновенных значений токов и напряжений во всх ветвях схемы.

В.2.1. Определим вначале комплексы действующих величин ЭДС, токов и напряжений во всех ветвях для первых трех нулевых гармоник.

В.2.1.1. 1 – я гармоника.

e_{A (1)} E_{A (1)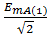} = = 103.1687e ^j0°

e_{B (1)} E_{B (1)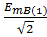} = e ^–j120° = 103.1687е ^–j120°

e_{C (1)} E_{C (1)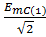} = e ^j120 = 103.1687e ^j120°

Z = 0 + j8 = 8e ^j90° Ом

Z₁ = 15 – j15 = 21.2132e ^–j45° Ом

Z₂ = 10 – j0 = 10e ^j0° Ом

Z'₁ = 15 – j15 = 21.2132e ^–j45° Ом

Z'₂ = 3.3333 + j0 = 3.3333e ^j0° Ом

Z_12зв = Z'₁ Z'₂ / (Z'₁ + Z'₂) = 21.2132e ^–j45° 3.3333e ^j0° / (15 – j15 + 3.3333 + j0) = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_A1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_В1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_С1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_Aобщ = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_Вобщ = 2.9703 + j7.7030= 8.2558e ^j68.91° Ом

Z_Собщ = 2.9703 + j7.7030 = 8.2558e ^j68.91° Ом

Z_A1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_В1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

Z_С1 = 2.9703 – j0.2970 = 2.9851e ^–j5.71° Ом

и смещение точки О₁ относительно О:

U_ONO = (103.2e ^j0° 3.3500 10 ^-1 e ^j5.71° + 103.2e ^–j120° 1.2113 10 ^-1 e ^–j68.91° + 103.2e ^j120° 1.2113 10 ^-1 e ^–j68.91° / (0.3333 + j0.333 + 0.0436 – j0.1130 + 0.0436 – j0.1130) = 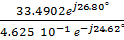= 72.4045e ^j51.42° = 45.1540 + j56.5997

Вычисляем токи ветвей:

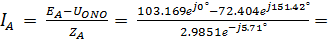27.1517e ^–j38.58°

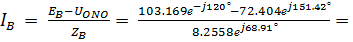21.2088e ^j167.55°

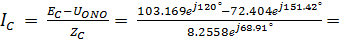12.3708e ^j92.39°

Проверяем равенство нулю векторной суммы всех токов (истинность первого уравнения Кирхгофа для узла О):

I_A + I_B + I_C = 21.2249 – j16.9327 - 20.7100 + j4.5727 – 0.5149 + j12.3600 = 0 + j0 = 0

Итак, баланс выполняется, т.е. токи найдены правильно.

Теперь вычислим токи через сопротивления Z₁, Z₂ в каждой ветви.

Падения напряжения между ключевыми точками:

U_A1ON = Z_А1 I_A = 2.9851e ^–j5.71° 27.1517e ^–j38.58° = 81.0508e ^–j44.29° B

U_B1ON = Z_В1 I_B = 2.9851e ^–j5.71° 21.2088e ^j167.55° = 63.3107e ^j161.84° B

U_C1ON = Z_С1 I_C = 2.9851e ^–j5.71° 12.3708e ^j92.39° = 36.9281e ^j86.67° B

U_A1B1 = U_A1ON - U_B1ON = 58.0147 – j56.5997 – (- 60.1567 + j19.7338) = 118.1714 – j76.3335 = 140.6814e ^–j32.86° B

U_B1C1 = U_B1ON - U_C1ON = - 60.1567 + j19.7338 – (2.1420 + j36.8659) = -62.2987 – j17.1321 = 64.6114e ^–j164.62° B

U_C1A1 = U_C1ON - U_A1ON = 2.1420 + j36.8659 – (58.0147 – j56.5997) = -55.8727 + j93.4656 = 108.8925e ^j120.87° B

Токи соответствующих разветвлений:

Между точками А1, В1, С1 – симметричная звезда из Z1. Мысленно заменяем ее эквивалентным симметричным треугольником из сопротивлений 3 Z1. Тогда 'фиктивные' токи между узлами А1, В1, С1:

I_A1B1 = U_A1B1 / 3 Z₁ = 140.6814e ^–j32.86° / 3 21.2132e ^-j45° = 2.2106e ^j112.14° A

I_B1C1 = U_B1C1 / 3 Z₁ = 64.6114e ^–j32.86° / 3 21.2132e ^-j45° = 1.0153e ^–j119.62° A

I_C1A1 = U_C1A1 / 3 Z₁ = 108.8925e ^j120.87° / 3 21.2132e ^-j45° = 1.7111e ^j165.87° A

а токи в фазах реальной звезды:

I_AZ1 = I_A1B1 – I_C1A1 = (2.1612 + j0.4649) – (- 1.6593 + j0.4177) = 3.8205 + j0.0472 = 3.8208e ^j0.71° A

I_BZ1 = I_B2C1 – I_A1B1 = (-0.5019 - j0.8826) – (2.1612 + j0.4649) = -2.6630 – j1.3474 = 2.9845e ^–j153.16° A

I_CZ1 = I_C1A1 – I_B1C1 = (-1.6593 + j0.4177) – (- 0.5019 - j0.8826) = -1.1575 + j1.3003 = 1.7408e ^j131.67° A

I_B2C2 = U_B1C1 / Z₂ = 64.6114e ^–j164.62° / 10e ^j0° = 6.4611e ^–j164.62° A

I_A2B2 = U_A1B1 / Z₂ = 140.6814e ^–j32.86° / 10e ^j0° = 14.0681e ^–j32.86° A

I_C2A2 = U_C1A1 / Z₂ = 108.8925e ^j120.87° / 10e ^j0° = 10.8892e ^j120.87° A

Токи в линейных проводах блока с Z2:

I_AZ2 = I_A2B2 – I_C2A2 = (11.8171 + j7.6333) – (- 5.5873 + j9.3466) = 17.4044 – j16.9799 = 24.3152e ^–j44.29° A

I_BZ2 = I_B2C2 – I_A2B2 = (-6.2299 – j1.7132) – (11.8171 + j7.6333) = -18.0470 + j5.9201 = 18.9932e ^j161.84° A

I_CZ2 = I_C2A2 – I_B2C2 = (-5.5873+ j9.3466) – (- 6.2299 – j1.7132) = 0.6426 + j11.0598 = 11.0784e ^j86.67° A

U_AA1 = Z I_A = 0e ^j0 27.1517e ^–j38.58° = 0e ^–j38.58° B

U_BB1 = Z I_B = 8e ^j90 21.2088e ^j167.55° = 169.6706e ^–j102.45° B

U_CC1 = Z I_C = 8e ^j90 12.3708e ^j92.39° = 98.9660e ^–j177.61° B

В.2.1.3. Для третьей гармоники токи заведомо равны нулю, поэтому их не вычисляем.

В.2.1.5. 5 – я гармоника.

e_{A (5)} E_{A (5)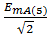} = = 4.1267e ^j0°

e_{B (5)} E_{B (5)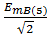} = e ^–j600° = 4.1267е ^–j600°

e_{C (5)} E_{C (5)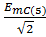} = e ^j600 = 4.1267e ^j600°

Z = 0 + j40 = 40e ^j90° Ом

Z₁ = 15 – j3 = 15.2971e ^–j11.31° Ом

Z₂ = 10 + j0 = 10e ^j0° Ом

Z'₁ = 15 – j3 = 15.2971e ^–j11.31° Ом

Z'₂ = 3.3333 + j0 = 3.3333e ^j0° Ом

Z_12зв = Z'₁ Z'₂ / (Z'₁ + Z'₂) = 15.2971e ^–j11.31° 3.3333e ^j0° / (15 – j3.3333 + j0) = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_A1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_В1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_С1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_Аобщ = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_Вобщ = 2.7431 + j39.9034 = 39.9976e ^j86.07° Ом

Z_Собщ = 2.7431 + j39.9034 = 39.9976e ^j86.07° Ом

Z_A1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_В1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

Z_С1 = 2.7431 – j0.0966 = 2.7448e ^–j2.02° Ом

и смещение точки О₁ относительно О:

U_ONO = (4.1e ^j0° 3.6433 10 ^-1 e ^j2.02° + 4.1e ^j600° 2.5002 10 ^-2 e ^–j86.07° + 4.1e ^j600° 2.5002 10 ^-2 e ^–j86.07° / (0.3641 + j0.0128 + 0.0017 – j0.0249 + 0.0017 – j0.0249) = 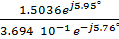= 4.0704e ^j11.71° = 3.9857 + j0.8260

Вычисляем токи ветвей:

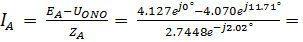0.3053е ^–j78.29°

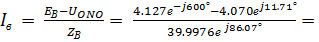0.1661е ^j69.50°

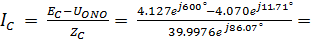0.1870е ^j129.96°

Проверяем равенство нулю векторной суммы всех токов (истинность первого уравнения Кирхгофа для узла 0):

I_A + I_B + I_C = 0,0619 – j0.2989 + 0.0582 + j0.1556 – 0.1201 + j0.1433 =- 0 - j0 = 0e ^–j92.35°

Итак, баланс выполняется, т.е. токи найдены правильно.

Теперь вычислим токи через сопротивления Z₁, Z₂ в каждой ветви.

Падения напряжения между ключевыми точками:

U_A1ON = Z_А1 I_A = 2.7448e ^–j2.02° 0.3053e ^–j78.29° = 0.8379e ^–j80.31° B

U_B1ON = Z_В1 I_B = 2.7448e ^–j2.02° 0.1661e ^j69.50° = 0.4559e ^j67.49° B

U_C1ON = Z_С1 I_C = 2.7448e ^–j2.02° 0.1870e ^j129.96° = 0.5133e ^j127.95° B

U_A1B1 = U_A1ON - U_B1ON = 0.1411 – j0.8260 – (0.1746 + j0.4212) = -0.0335 – j1.2471 = 1.2476e ^–j91.54° B

U_B1C1 = U_B1ON - U_C1ON = 0.1746 + j0.4212 – (-0.3156 + j0.4048) = 0.4902 + j0.0164 = 0.4905e ^j1.92° B

U_C1A1 = U_C1ON - U_A1ON = -0.3156 + j0.4048 – (0.1411 – j0.8260) = -0.4567 + j1.2307 = 1.3127e ^j110.36° B

Токи соответствующих разветвлений:

Между точками А1, В1, С1 – симметричная звезда из Z1. Мысленно заменяем ее эквивалентным симметричным треугольником из сопротивлений 3 Z1. Тогда 'фиктивные' токи между узлами А1, В1, С1:

I_A1B1 = U_A1B1 / 3 Z₁ = 1.2476e ^–j91.54° / 3 15.2971e ^–j11.31° = 0.0272e ^–j80.23° A

I_B1C1 = U_B1C1 / 3 Z₁ = 0.4905e ^j1.92° / 3 15.2971e ^–j11.31° = 0.0107e ^j13.23° A

I_C1A1 = U_C1A1 / 3 Z₁ = 1.3127e ^j110.36° / 3 15.2971e ^–j11.31° = 0.0286e ^j121.67° A

а токи в фазах реальной звезды:

I_AZ1 = I_A1B1 – I_C1A1 = (0.0046 - j0.0268) – (- 0.0150 + j0.0243) = 0.0196 - j0.0511 = 0.0548e ^–j69.00° A

I_BZ1 = I_B2C1 – I_A1B1 = (0.0140 + j0.0024) – (0.0046 - j0.0268) = 0.0058 + j0.0292 = 0.0298e ^j78.79° A

I_CZ1 = I_C1A1 – I_B1C1 = (-0.0150 + j0.0243) – (0.0104 + j0.0024) = -0.0254 + j0.0219 = 0.0336e ^j139.26° A

I_B2C2 = U_B1C1 / Z₂ = 0.4905e ^j1.92° / 10e ^j0° = 0.0491e ^j1.92° A

I_A2B2 = U_A1B1 / Z₂ = 1.2476e ^–j91.54° / 10e ^j0° = 0.1248e ^–j91.54° A

I_C2A2 = U_C1A1 / Z₂ = 1.3127e ^j110.36° / 10e ^j0° = 0.1313e ^j110.36° A

Токи в линейных проводах блока с Z2:

I_AZ2 = I_A2B2 – I_C2A2 = (-0.0034 – j0.1247) – (-0.0457 + j0.1231) = 0.0423 – j0.2478 = 0.2515e ^–j80.31° A

I_BZ2 = I_B2C2 – I_A2B2 = (0.0490 + j0.0016) – (-0.0034 – j0.1247) = 0.0524 + j0.1264 = 0.1368e ^j67.49° A

I_CZ2 = I_C2A2 – I_B2C2 = (-0.0457 + j0.1231) – (0.0490 + j0.0016) = -0.0947 + j0.1214 = 0.1540e ^j127.95° A

U_AA1 = Z I_A = 0e ^j0 0.3053e ^–j78.29° = 0e ^–j78.29° B

U_BB1 = Z I_B = 40e ^j90 0.1661e ^j69.50° = 6.6444e ^j159.50° B

U_CC1 = Z I_C = 40e ^j90 0.1870e ^j129.96° = 7.4804e ^–j140.04° B

В.2.2. Запишем теперь выражения для мгновенных значений токов, протекающих через элементы схемы, и падения напряжений на этих элементах, учитывая, что амплитуда гармоник больше модулей комплексов соответствующих действующих значений в 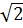раз:

i_A(t) = 38.40 Sin (ωt – 38.58°) + 0.43 Sin (5ωt – 78.29°)

i_B(t) = 29.99 Sin (ωt + 167.55°) + 0.23 Sin (5ωt + 69.50°)

i_C(t) = 17.49 Sin (ωt + 92.39°) + 0.26 Sin (5ωt + 129.96°)

i_AZ1(t) = 5.40 Sin (ωt + 0.71°) + 0.08 Sin (5ωt - 69°)

i_BZ1(t) = 4.22 Sin (ωt – 153.16°) + 0.04 Sin (5ωt + 78.79°)

i_CZ1(t) = 2.46 Sin (ωt + 131.67°) + 0.05 Sin (5ωt + 139.26°)

i_ABZ2(t) = 19.90 Sin (ωt – 32.86°) + 0.18 Sin (5ωt – 91.54°)

i_BCZ2(t) = 9.14 Sin (ωt – 164.62°) + 0.07 Sin (5ωt + 1.92°)

i_CAZ2(t) = 15.40 Sin (ωt + 120.87°) + 0.19 Sin (5ωt + 110.36°)

U_AZ(t) = 0 Sin (ωt – 38.58°) + 0 Sin (5ωt – 78.29°)

U_BZ(t) = 239.95 Sin (ωt – 102.45°) + 9.40 Sin (5ωt + 159.50°)

U_CZ(t) = 139.96 Sin (ωt – 177.61°) + 10.58 Sin (5ωt – 140.04°)

U_AZ1(t) = 114.62 Sin (ωt – 44.29°) + 1.18 Sin (5ωt – 80.31°)

U_BZ1(t) = 89.53 Sin (ωt + 161.84°) + 0.64 Sin (5ωt + 67.49°)

U_CZ1(t) = 52.22 Sin (ωt + 86.67°) + 0.73 Sin (5ωt + 127.95°)

U_ABZ2(t) = 198.95 Sin (ωt – 32.86°) + 1.76 Sin (5ωt – 91.54°)

U_BCZ2(t) = 91.37 Sin (ωt – 164.62°) + 0.69 Sin (5ωt + 1.92°)

U_CAZ2(t) = 154 Sin (ωt + 120.87°) + 1.86 Sin (5ωt + 110.36°)

B.3. Определяем показания амперметра электродинамической системы по формуле

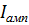
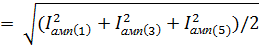
Запишем комплексы амплитуд отдельных гармоник:

I_{амперметр (1)} = 26.8605e ^j161.84° A

I_{амперметр (3)} = 0e ^j0° A

I_{амперметр (5)} = 0.1934e ^j67.49° A

тогда

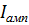
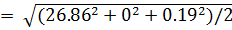= 18.99 А

Запишем выражение для тока в ветви с амперметром:

i_амп (t) = 26.860Sin (ωt + 161.84°) + 0.193Sin (5ωt + 67.49°) (см.рис.12)

B.4. Определяем мощность измеряемую ваттметрами для ваттметра W1 в 1 – й ветви по формуле

P = Re (S_W1),

S_W1 = Ʃ_1,3,5 U_W1 I_W1* = U_W1(1) I*_{W1 (1)} + U_W1(3) I*_W1(3) + U_W1(5) I*_W1(5)

для ваттметра W2 в 2 – й ветви по формуле

P = Re (S_W2),

S_W2 = Ʃ_1,3,5 U_W2 I_W2* = U_W2(1) I*_{W2 (1)} + U_W2(3) I*_W2(3) + U_W2(5) I*_W2(5)

где суммирование идет по всем гармоникам. Учитывая, что токи третьей гармоники равны нулю, получим

U_{W1 (1)} = 108.89e ^–j59.13° B

I_{W1 (1)} = 27.1517e ^–j38.58° A

U_{W1 (1)} I*_W1(1) = 2956.61e ^–j20.55° B A

U_{W1 (5)} = 1.31e ^–j69.64° B

I_{W1 (5)} = 0.3053e ^–j78.29° A

U_{W1 (5)} I*_W1(5) = 0.40e ^j8.65° B A

S_W1 = 2956.9634e ^–j20.54° = 2768.9163 – j1037.6585

P_W1 = 2768.92 Вт

U_W2(1) = 64.61e ^–j164.62° B

I_W2(1) = 21.2088e ^j167.55° A

U_W2(1) I*_W2(1) = 1370.33e ^j27.83° B A

U_W2(5) = 0.49e ^j1.92° B

I_W2(5) = 0.1661e ^j69.50° A

U_W2(5) I*_W2(5) = 0.08e ^–j67.59° B A

S_W2 = 1970.3245e ^j27.82° = 1211.8973 + j639.6048

P_W2 = 1211.90 Вт

B.5. Строим векторные диаграммы для всех гармоник (рис.13, 14).

 

Рис.1б (схема 1)

 

 

 

 

1. Найдем разложение функции f (ωt), график которой изображен на рис.1б, в ряд Фурье:

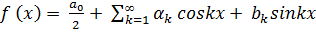(1)

Так как заданная функция нечетна, то она содержит в своем разложении только синусы, так что

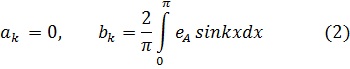
Руководствуясь видом функции на графике, запишем аналитическое представление для кусочно заданной на участке (0, π) функции:

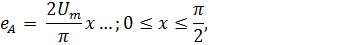
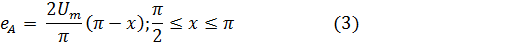
Подставляя аналитическое определение (3) в интегралы (2), пoлучим

 

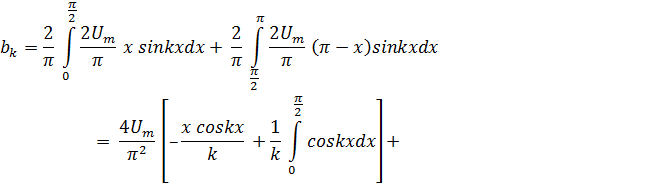
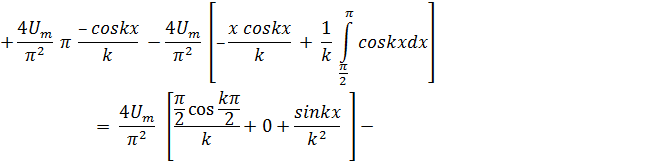
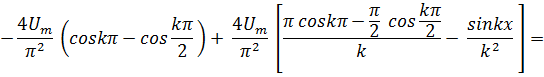
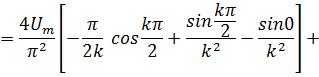
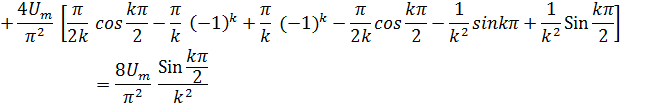
При четных k = 21 (1=0,1,2…),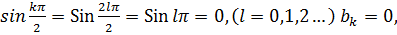

При нечетных k = 21+1, 1=0,1,2…

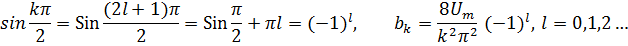
Таким образом, место х в (1) подставляем ωt и учитываем только первые три гармоники, получим входной сигнал: