Магнитоэлектрические измерительные механизмы

В магнито­электрических измерительных механизмах вращающий момент соз­дается в результате взаимодействия магнитного поля постоянного магнита и магнитного поля проводника с током, выполняемого обычно в виде катушки. Применяются как измерительные механизмы с под­вижной катушкой и неподвижным магнитом, так и измерительные механизмы с неподвижной катушкой и подвижным магнитом. Больше распространены измерительные механизмы с подвижной катушкой.

Основными узлами магнитоэлектрического измерительного ме­ханизма являются магнитная система и подвижная часть. В зави­симости от взаимного расположения постоянного магнита и подвиж­ной катушки различают измерительные механизмы с внешним маг­нитом и с внутрирамочным магнитом.

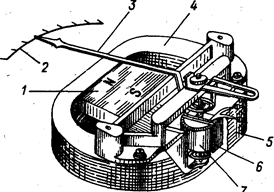
Рис. 5 – Устройство магнитоэлектрического прибора с подвижной рамкой

Магнитная система с внешним магнитом (рис.5) состоит из постоянного магнита 1, магнитопровода 4, полюсных наконечников 5 и неподвижного сердечника 7.

В воздушном зазоре располагается рамка 6. Она свободно охватывает сердечник и жестко крепится на полуосях, поворот которых вызывает перемещение стрелки 3 над шкалой 2. Рамка имеет обмотку из медного или алюминиевого изо­лированного провода диаметром от 0,03 до 0,2 мм и чаще всего бывает прямоуголь­ной формы. Применяются бескаркасные и каркасные рамки.

В бескаркасной рамке необходимая жесткость катушки обеспечивается пу­тем склеивания ее витков бакелитовым лаком. В каркасных рамках обмотка на­матывается на каркас, выполняемый из алюминия, толщиной порядка 0,1—0,2 мм. Каркас необходим для того, чтобы увеличить механическую прочность райки, но также и для получения нужного успокоения подвижной части. В магнито­электрических измерительных механизмах используется магнитоиндукционное успокоение, но без применения специальных успокоителей. При движении рамки в поле постоянного магнита момент успокоения создается за счет взаимодействия вихревых токов, возникающих в цепи обмотки рамки, с полем магнита. Этот мо­мент зависит от величины внешнего сопротивления, на которое включена обмотка рамки, и имеет незначительную величину. Для увеличения момента успокоения на рамку наматывается несколько короткозамкнутых витков.

Если же этого недостаточно, то применяется металлический каркас, представляющий собой в электрическом отношении как бы один короткозамкнутых виток.

Влияние трения рамки о воздух на ве­личину успокоения незначительно.

На рис. 6 представлена магнитная си­стема с внутрирамочным магнитом. Она со­стоит из магнита 1, полюсных наконечников 2, служащих для получения равномерного ради­ального поля в рабочем воздушном зазоре, и ярма 3, являющегося одновременно магнит­ным экраном.

В системах с внутрирамочным магнитом по сравнению с системами с внешним магни­том значительно меньше потоки рассеяния и, следовательно, лучше используется энергия магнита. Применение такой магнитной систе­мы позволяет создать приборы малого веса и габарита.

К недостаткам систем с внутрирамочным магнитом следует отнести то, что магнитное поле в воздушном зазоре по величине и одно­родности уступает полю, которое может быть получено в системах с внешним магнитом. Это объясняется относительно малым возможным объемом внутрирамочного магнита и трудностями выравнивания поля. В связи с этим по точности и чувствительности приборы с внутрирамочным магнитом пока усту­пают приборам с внешним магнитом.

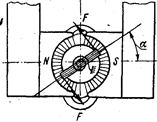
На рис. 7 показана подвижная рамка измерительного механизма, находящаяся в радиальном магнитном поле. При протекании по об­мотке рамки тока возникают силы F, стремящиеся повернуть рамку так, чтобы ее плоскость стала перпендикулярной к направлению магнитных силовых линий. При равенстве вращающего и противодействующего мо­ментов подвижная часть останавливается.

	Рис. 7. Подвижная катушка в радиальном магнитном поле

Для получения зависимости между углом отклонения и силой постоянного тока в рамке воспользуемся основными положениями.

Применительно к нашему случаю вы­ражение (2) для вращающего, момента представляется так:

(5)

где Ф — поток, сцепляющийся с обмоткой рамки; I — ток в обмотке рамки.

Величина Ф может быть подсчитана как произведение В в воздушном зазоре, числа витков w обмотки рамки и суммы двух боковых поверхностей, описанных активными сторонами подвижной катушки при ее повороте на угол a от нейтрального положения.

В соответствии с рис. 7 активными сторонами обмотки рамки будут являться стороны, расположенные в плоскости, перпендикулярной рисунку. Стороны рамки, находящиеся в плоскости рисунка, при своем движении скользят вдоль силовых линий, не пересекая их, и поэтому не будут участвовать в создании вращающего момента. Следовательно,

Ф = B2lωα (6)

где r — радиус рамки; I — длина рамки; a — угол поворота рамки от нейтрального положения.

Обозначив площадь катушки через s, можем написать

Ф = Bsωα (7)

Подставляя это выражение в формулу (5) и дифференцируя его, получим

M = BsωI. (8)

Так как противодействующий момент создается пружинками, то можно воспользоваться формулой (3) и для режима установившегося отклонения написать

BsωI = W_α,

откуда

(9)

Из выражения (9) и определения понятия чувствительности следует, что для магнитоэлектрических приборов

(10)

Из уравнения (10) видно, что чувствительность магнитоэлектри­ческого прибора не зависит от угла отклонения и постоянна по всей шкале.

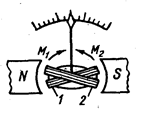
Рис. 8 – Устройство измерительного меха­низма магнитоэлектрического логометра

Преимущества магнитоэлектрических приборов:

- относятся к числу наиболее точных приборов;

- высокая чувствительность;

- малое собственное потребление мощности.

Недостатки магнитоэлектрических приборов:

- сложная и дорогая конструкция;

- невысокая перегрузочная способность.

На рис.8 изображен магнитоэлектрический логометр.

Подвижная часть выполняется в виде двух жестко скрепленных между собой рамок 1 и 2, по обмоткам которых протекают токи I ₁ и I ₂. Пружинки для соз­дания механического противодействующего момента не ставятся, а ток к обмоткам подводится с помощью безмоментных токоподводов, выполняемых в виде тонких неупругих ленточек.

Выражения для моментов М₁ и М₂ могут быть записаны так:

М₁ = k₁F₁(α)I₁;

М₂ = k₂F₂(α)I₂,

где k₁=s₁w₁; k₂=s₂w₂; F₁(a) и F₂(a) — функции, выражающие закон изменения индукции для рамок 1 и 2 при перемещении их в зазоре. При установившемся равновесии моменты M₁ и М₂, равны, т. е.

k₁F₁(α)I₁ = k₂F₂(α)I₂

откуда

или, обозначив

и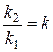

получим

Выражение для обратной функции:

(11)