2.1. Алгоритм перевода целых десятичных чисел
в двоичную систему счисления
Алгоритм перевода целого десятичного числа в двоичное будет следующим:
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньшее 2.
Записать полученные остатки вобратной последовательности.
В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в табл. 2:
Таблица 2
Пример перевода целого десятичного числа
в двоичную систему счисления
| Десятичное число/ целое частное | Делитель (основание системы) | Остаток | Цифры двоичного числа |
 a0 a0
| |||
| a1 | |||
| a2 | |||
| a3 | |||
| a4 |
В результате получаем двоичное число:
N2 = a4 a3 a2 a1 a0 = 100112
2.2. Алгоритм перевода правильных десятичных дробей
в двоичную систему счисления.
Алгоритм перевода правильной десятичной дроби в двоичную будет следующим:
1. Последовательно выполнять умножение исходной десятичной дроби и получаемых дробных частей произведений на основание системы (на 2) до тех пор, пока не получится нулевая дробная часть или не будет достигнут требуемая точность вычислений.
2. Записать полученные целые части произведения в прямой последовательности.
В качестве примера рассмотрим перевод десятичной дроби 0,75 в двоичную систему, записывая результаты в табл. 3:
Таблица 3
Пример перевода правильной десятичной дроби
в двоичную систему счисления
| Десятичная дробь/ дробная часть произведения | Множитель (основание системы) | Целая часть произведения | Цифры двоичного числа |
| 0,75 |  a-1 a-1
| ||
| 0,50 | a-2 | ||
| 0,00 |
В результате получаем двоичную дробь:
N2 = 0,а-1 а-2 = 0,112.
2.3. Перевод чисел из системы с основанием р
в систему с основанием q.
Перевод чисел из позиционной системы с произвольным основанием р в систему с основанием q производится по алгоритмам, аналогичным рассмотренным выше.
Рассмотрим алгоритм перевода целых чисел на примере перевода целого десятичного числа N10 = 42410 в шестнадцатеричную систему, то есть из системы счисления с основанием р = 10 в систему счисления с основанием q = 16.
В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае шестнадцатеричной) (табл. 4).
Таблица 4
Пример перевода целого десятичного числа
в шестнадцатеричную систему счисления
| Десятичное число/ целое частное | Делитель (основание системы) | Остаток | Цифры двоичного числа |
 a0 a0
| |||
| 10 (A) | a1 | ||
| a2 |
В результате получаем шестнадцатеричное число:
N16 = a2 a1 a0 = 1А816.
Рассмотрим теперь алгоритм перевода дробных чисел на примере перевода десятичной дроби N10 = 0,40625 в восьмеричную систему, то есть из системы счисления с основанием р = 10 в систему счисления с основанием q = 8.
В процессе выполнения алгоритма необходимо обратить внимание, что все действия необходимо осуществлять в исходной системе счисления (в данном случае десятичной), а полученные остатки записывать цифрами новой системы счисления (в данном случае восьмеричной) (табл. 5).
Таблица 5
Пример перевода правильной десятичной дроби
в восьмеричную систему счисления
| Десятичная дробь/ дробная часть произведения | Множитель (основание системы) | Целая часть произведения | Цифры двоичного числа |
| 0,40625 |  a-1 a-1
| ||
| 0,25 | a-2 | ||
| 0,00 |
В результате получаем восьмеричную дробь:
N8 = 0,а-1 а-2 = 0,32 8.
Перевод чисел, содержащих и целую и дробную части, производится в два этапа. Отдельно переводится по соответствующему алгоритму целая часть и отдельно — дробная. В итоговой записи полученного числа целая часть от дробной отделяется запятой.
2.4. Перевод чисел из двоичной системы счисления
в восьмеричную и шестнадцатеричную и обратно
Перевод чисел между системами счисления, основания которых являются степенями числа 2, может производиться по более простым алгоритмам. Такие алгоритмы могут применяться для перевода чисел между двоичной (q = 21), восьмеричной (q = 23) и шестнадцатеричной (q = 24) системами счисления.
2.4.1. Перевод чисел из двоичной системы счисления в восьмеричную. Для записи двоичных чисел используются две цифры, то есть в каждом разряде числа возможны 2 варианта записи. Решаем показательное уравнение:
2 = 2I. Так как 2 = 21, то I = 1 бит.
Каждый разряд двоичного числа содержит 1 бит информации.
Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение:
8 = 2I. Так как 8 = 23, то I = 3 бита.
Каждый разряд восьмеричного числа содержит 3 бита информации.
Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012 → 1∙22 + 0∙21 + 1∙20 0∙22 + 0∙21 + 1∙20 → 518
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) ввосьмеричные цифры (табл. 6):
Таблица 6
Преобразование двоичных триад в восьмеричные цифры
| Двоичные триады | ||||||||
| Восьмеричные цифры |
Для перевода дробного двоичного числа (правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой группе окажется меньше трех цифр, дополнить ее справа нулями. Далее необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число N2 = = 0,1101012 в восьмеричную систему счисления (табл. 7):
Таблица 7
| Двоичные триады | ||
| Восьмеричные цифры |
Получаем: N8 = 0,658.
2.4.2. Перевод чисел из двоичной системы счисления в шестнадцатеричную. Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи. Решаем показательное уравнение:
16 = 2I. Так как 16 = 24, то I= 4 бита.
Каждый разряд шестнадцатеричного числа содержит 4 бита информации.
Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если впоследней, левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.
Затем надо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр (табл. 8).
Таблица 8
Соответствие двоичных тетрад и шестнадцатеричных цифр
| Двоичные тетрады | ||||||||
| Шестнадцатеричные цифры | ||||||||
| Окончание таблицы №8 | ||||||||
| Двоичные тетрады | ||||||||
| Шестнадцатеричные цифры | A(10) | B(11) | C(12) | D(13) | E(14) | F(15) |
Переведем целое двоичное число N2 = 1010012 в шестнадцатеричное (табл. 9).
Таблица 9
| Двоичные тетрады | ||
| Шестнадцатеричные цифры |
В результате имеем: N16 = 2916.
Переведем дробное двоичное число N2= 0,1101012 в шестнадцатеричную систему счисления (табл. 10).
Таблица №10
| Двоичные тетрады | ||
| Шестнадцатеричные цифры | D |
Получаем: N16 = 0,D416.
Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.
2.5. Перевод чисел из восьмеричной и шестнадцатеричной
систем счисления в двоичную
Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа — в группу из четырех цифр (тетраду).
Например, преобразуем дробное восьмеричное число N8 = = 0,478 в двоичную систему счисления (табл. 11).
Таблица 11
| Восьмеричные цифры | ||
| Двоичные триады |
Получаем: N2 = 0,1001112
 Переведем целое шестнадцатеричное число N16 = AB16 в двоичную систему счисления (табл. №12).
Переведем целое шестнадцатеричное число N16 = AB16 в двоичную систему счисления (табл. №12).
Таблица 12
| Шестнадцатеричные цифры | А | В | |
| Двоичные тетрады | |||
В результате имеем: N2 = 101010112.
Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения (табл. 13).
Таблица 13
Арифметические действия над двоичными числами
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0 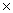 0=0 0 0=0 0 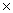 1=0 1 1=0 1 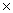 0=0 1 0=0 1  1=1 1=1
|
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и перенос из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Пример. Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
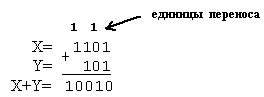
Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;

Результат 1101+101+111=11001.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.

Результат 10010 - 101=1101.
Умножение двоичных чисел производится по тем же правилам, что и для десятичных, с помощью таблиц двоичного умножения и сложения.
Пример. 1001  101=?
101=?

Результат 1001  101=101101.
101=101101.
Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.
Пример. 1100.011: 10.01=?

Результат 1100.011: 10.01=101.1.
Задание 1.
Перевести следующие числа в десятичную систему счисления.
Таблица 14
| Номер задания | ()2 | ()8 | ()16 |
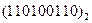
| 
| 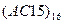
| |
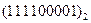
| 
| 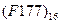
| |
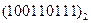
| 
| 
| |
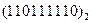
| 
| 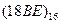
| |

| 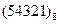
| 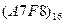
| |

| 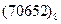
| 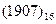
| |
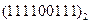
| 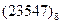
| 
| |
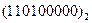
| 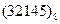
| 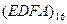
| |
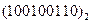
| 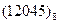
| 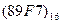
| |
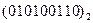
| 
| 
| |
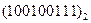
| 
| 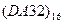
| |
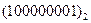
| 
| 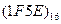
| |

| 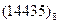
| 
| |
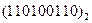
| 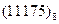
| 
| |
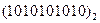
| 
| 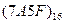
| |

| 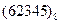
| 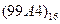
| |

| 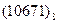
| 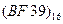
| |

| 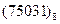
| 
| |

| 
| 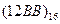
| |
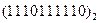
| 
| 
| |
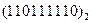
| 
| 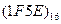
| |

| 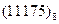
| 
| |
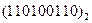
| 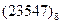
| 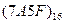
| |
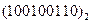
| 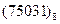
| 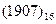
| |

| 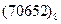
| 
| |
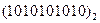
| 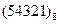
| 
| |
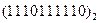
| 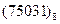
| 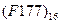
| |
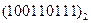
| 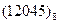
| 
| |

| 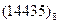
| 
| |
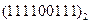
| 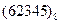
| 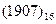
| |
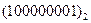
| 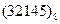
| 
| |

| 
| 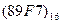
| |
| Окончание таблицы 14 | |||

| 
| 
|
Задание 2
Перевести в различные системы счисления из десятичной системы.
Таблица 15
| Номер задания | ()2 | ()8 | ()16 |
Задание 3
Перевести следующие числа из "10" с.с. в "2", "8", "16" с.с. (точность вычислений - 5 знаков после точки).
Таблица 16
| Номер задания | ()2 | ()8 | ()16 |
| 89.7865 | 26.83638 | 71.82557 | |
| 20.5776 | 85.27481 | 81.24015 | |
| 13.73132 | 5.012013 | 80.60332 | |
| 76.4339 | 44.11573 | 26.38159 | |
| 78.45395 | 81.69169 | 14.68738 | |
| 17.37239 | 15.2214 | 65.88041 | |
| 35.34158 | 10.4597 | 32.59281 | |
| 10.78611 | 45.80574 | 15.15715 | |
| 51.55492 | 79.32604 | 79.49258 | |
| 42.00625 | 82.18332 | 17.77342 | |
| 64.50671 | 43.50781 | 73.86342 | |
| 41.5236 | 11.36643 | 33.80041 | |
| 24.42148 | 50.8255 | 74.97336 | |
| 64.4697 | 78.33991 | 34.50648 | |
| 78.05792 | 97.34678 | 9.263874 | |
| 28.01141 | 63.87399 | 1.635239 | |
| 21.1466 | 27.58419 | 80.81452 | |
| 1.900355 | 25.47041 | 0.485862 | |
| 84.51437 | 65.98507 | 92.7803 | |
| 36.78392 | 60.49811 | 16.43428 | |
| 76.02919 | 73.06626 | 22.18313 | |
| 3.805754 | 4.861077 | 81.64203 | |
| 97.44221 | 61.77253 | 27.53602 | |
| 1.040206 | 89.16717 | 52.40544 | |
| 36.99126 | 31.86707 | 94.97233 | |
| 12.28652 | 87.58477 | 44.3591 | |
| 87.0619 | 91.13255 | 71.88561 | |
| 56.02728 | 33.92358 | 9.725709 | |
| 65.02889 | 84.63753 | 37.32031 | |
| 69.89317 | 46.30993 | 43.8877 | |
| 41.98384 | 30.99016 | 42.23452 | |
| 44.44666 | 75.49326 | 6.343357 | |
| 31.78583 | 40.44453 | 19.23946 |
Задание 4. Перевести следующие числа в двоичную с. счисления.
Таблица 17
| Номер задания | ()8 | ()16 |

| 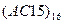
| |

| 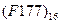
| |

| 
| |

| 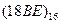
| |
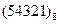
| 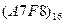
| |
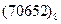
| 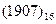
| |
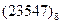
| 
| |
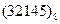
| 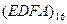
| |
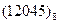
| 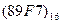
| |

| 
| |

| 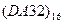
| |

| 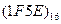
| |
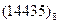
| 
| |
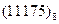
| 
| |

| 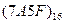
| |
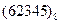
| 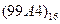
| |
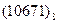
| 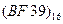
| |
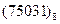
| 
| |

| 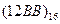
| |

| 
| |

| 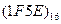
| |
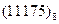
| 
| |
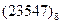
| 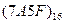
| |
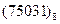
| 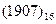
| |
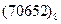
| 
| |
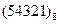
| 
| |
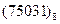
| 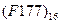
| |
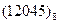
| 
| |
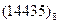
| 
| |
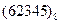
| 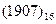
| |
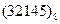
| 
| |

| 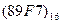
| |

| 
|
Задание 5 (табл. 18)
Перевести следующие числа в восьмеричную систему счисления:
Таблица 18
| Номер задания | ()2 | ()10 | ()16 |
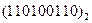
| 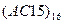
| ||
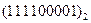
| 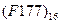
| ||
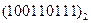
| 
| ||
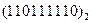
| 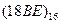
| ||

| 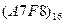
| ||

| 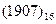
| ||
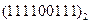
| 
| ||
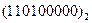
| 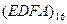
| ||
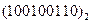
| 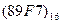
| ||
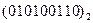
| 
| ||
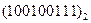
| 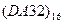
| ||
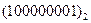
| 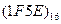
| ||

| 
| ||
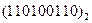
| 
| ||
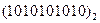
| 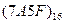
| ||

| 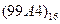
| ||

| 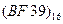
| ||

| 
| ||

| 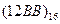
| ||
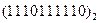
| 
| ||
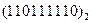
| 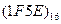
| ||

| 
| ||
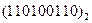
| 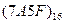
| ||
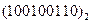
| 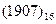
| ||

| 
| ||
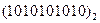
| 
| ||
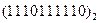
| 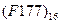
| ||
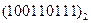
| 
| ||

| 
| ||
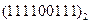
| 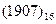
| ||
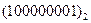
| 
| ||

| 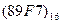
| ||

| 
|
Задание 6 (табл. 19)
Перевести следующие числа в шестнадцатиричную систему счисления:
Таблица 19
| Номер задания | ()2 | ()8 | ()10 | |
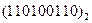
| 
| |||
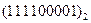
| 
| |||
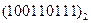
| 
| |||
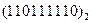
| 
| |||

| 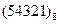
| |||

| 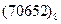
| |||
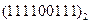
| 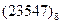
| |||
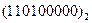
| 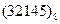
| |||
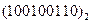
| 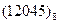
| |||
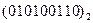
| 
| |||
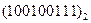
| 
| |||
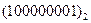
| 
| |||

| 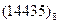
| |||
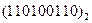
| 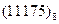
| |||
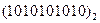
| 
| |||

| 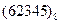
| |||

| 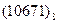
| |||

| 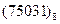
| |||

| 
| |||
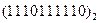
| 
| |||
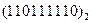
| 
| |||

| 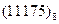
| |||
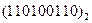
| 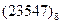
| |||
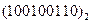
| 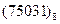
| |||

| 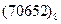
| |||
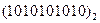
| 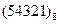
| |||
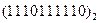
| 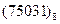
| |||
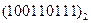
| 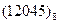
| |||

| 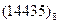
| |||
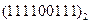
| 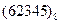
| |||
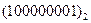
| 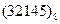
| |||
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-08-20 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |