Материал для 5-6 классов.

Учимся решать комбинаторные задачи

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Комбинаторная задача - это задача, в которой требуется либо перебрать все возможные варианты для той или иной операции, либо определить число таких вариантов, либо сделать и то и другое.

Например, для задачи: «Сколько двузначных чисел можно составить из цифр 1, 2 и 3?» перебор вариантов возможен при помощи:

единицы

таблицы или ориентированного графа.

десятки

●

●

●

Ответ: 9 чисел. (Каждое ориентированное ребро графа обозначает число. Всего 9 ребер, значит и чисел 9.)

Граф – это фигура, состоящая из точек и отрезков, соединяющих некоторые из этих точек. Точки называются вершинами графа, а отрезки – ребрами графа.

Ребро графа называют ориентированным, если одну вершину считают началом ребра, а другую концом. На рисунке ориентированное ребро изображают стрелкой.

 

Комбинаторные задачи также можно решать с помощью дерева возможных вариантов и с помощью правила умножения.

Рассмотрим вариант решения с помощью построения специальной схемы – так называемого дерева возможных вариантов. Это название принято потому, что такая схема действительно напоминает дерево, правда, расположенное «вверх ногами» и без ствола. Корень дерева изображают знаком ∗.

Задача 1. «Сколько трехзначных чисел можно составить из цифр 3, 4 и 5 при условии, что цифры в записи числа не повторяются?» дерево возможных вариантов будет таким:

						∗
Сотни		·				·				·
Десятки	· 4		·		·		·		·		·
Единицы	·		·		·		·		·		·
Числа

 

Ответ: из цифр 3, 4 и 5 при условии, что цифры в записи числа не повторяются можно составить 6 трехзначных чисел.

 

В чем заключается правило умножения?

Если первый элемент в комбинации можно выбрать а способами, после чего второй элемент b способами, а третий элемент с способами, то общее число комбинаций из трёх элементов будет a×b×c.

Для вышерассмотренной задачи первой цифрой числа (сотни) может быть любая из трёх данных цифр (3, 4, 5), второй (десятки) – любая из двух других. А третьей (единицы) – оставшаяся. Всего из данных цифр можно составить 3 × 2 × 1 = 6 трехзначных чисел.

 

Материал для 5-6 классов.

Уникурсальные фигуры

 

Уникурсальная фигура – это фигура, которую можно начертить одним росчерком, то есть, не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды.

Существует правило, позволяющее определить, можно ли начертить фигуру одним росчерком. Оно основывается на понятиях четной и нечетной вершины графа: вершину графа называют четной, если из нее исходит четное число ребер, и нечетной, если из нее исходит нечетное число ребер. Граф – это фигура, состоящая из конечного множества точек плоскости и отрезков, соединяющих некоторые из этих точек. Точки называются вершинами графа, а отрезки – ребрами графа.

Правило:

фигуру можно начертить одним росчерком, если:

1) все ее вершины четные, при этом движение можно начинать с любой вершины и закончить в той же вершине;

2) у нее только две нечетные вершины, при этом движение нужно начать с одной из этих нечетных вершин и закончить другой.

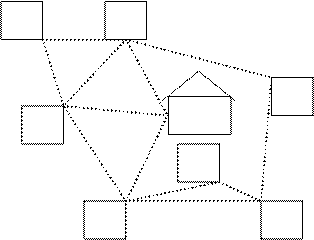
Вот пример задачи, где используется уникурсальная фигура.

почта

Почтальон Печкин разнес почту во все дома деревни и зашел к Дяде Фёдору выпить молока. На рисунке показаны все тропинки, которые проходил Печкин, причем по каждой тропинке он прошёл только один раз. Укажи номерами порядок прохождения тропинок, а стрелками – направление. В каком доме живёт Дядя Фёдор?

 

Применим вышеизложенное правило к данной задаче:

Вершина - является четной, т.к. она имеет четное число рёбер (четыре).

 

Вершины 2, 3, 4, 6, 7 – также четные.

Вершина 5 и вершина под названием «почта» – нечетные, т.к. они имеют нечетное количество рёбер (по три каждая).

Согласно пункту 2 вышеизложенного правила, мы имеет возможность весь путь «начертить одним росчерком», т.к. в нашей задаче только две нечетные вершины. При этом движение мы должны начать с одной из этих нечетных вершин и закончить другой.

Попробуем начать с вершины «почта» и закончить вершиной 5.

Ответ: п-1-3-п-7-1-2-3-4-5-6-7-5. Дядя Фёдор живет в домике №5.

Вывод: Математически доказано, что у почтальона Печкина в данной задаче есть возможность разнести всю почту по адресам, при этом проходить по каждой тропинке он будет только один раз.

 

При решении задач, по условию которых необходимо проложить маршрут, рекомендуется:

- построить граф;

- проверить его на правило для уникурсальных фигур;

- сделать вывод о наличии или отсутствии решения;

- если решение имеется, искать маршрут.