Варианты индивидуальных заданий 18
Библиографический список 24
Введение
Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №1.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы [1] – [3] и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Большое количество образцов решенных задач дано в руководстве к решению задач [5]. Задачи для самостоятельного решения имеются как в представленных методических указаниях, так и в сборниках задач [4], [6].
Номер варианта по каждому заданию студент выбирает по формуле 
,
где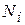 
- номер варианта,
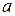- номер задания,
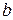- предпоследняя цифра шифра студента,
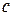- последняя цифра шифра.
Пример.
Пусть шифр студента 1235, тогда:
номер варианта первого задания: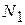 
= 
;
номер варианта второго задания: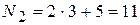 
;
номер варианта третьего задания: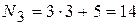 
;
номер варианта четвертого задания: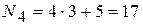 
.
Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая цифра по формуле получится число больше 20, то для определения варианта от полученной цифры отнимают 20.
Пример.
Пусть шифр студента 1298.
Номер варианта второго задания: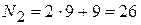 
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу вариант №6.
1 Решение систем линейных уравнений методами Крамера и Гаусса
Пусть дана система n уравнений с n неизвестными:
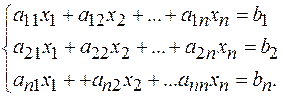
Основная матрица А такой системы квадратная. Определитель этой матрицы
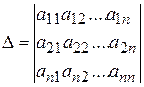
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной и имеет единственное решение.
|
|
В дальнейшем мы будем иметь дело только с такими системами.
Наиболее простым методом для решения таких систем линейных уравнений является метод Крамера.
Формулы Крамера имеют вид: 
(1.1.1)
Более универсальным и эффективным является метод Гаусса, состоящий в последовательном исключении неизвестных.
Решение осуществляется в два этапа: 1) система приводится к треугольному виду, 2) последовательно определяют неизвестные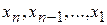 
.
Пример 1.
Решить систему уравнений методами Крамера и Гаусса:
Решение:
а) Метод Крамера.
Найдем определитель системы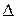 
, 
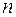. Предварительно сложив второй столбец с третьим и разложив определитель по элементам последнего столбца.
= 
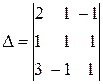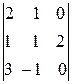=2(-1)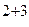 
=-2(-2-3)=10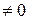 
.
Так как 
, то система имеет единственное решение.
Найдем определител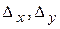и 
и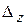 
, заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов (при вычислении определителя 
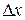преобразования аналогичные предыдущему.)
= 
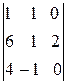=2(-1)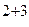 
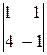-2(-1-4)=10.
При вычислении определителя 
последнюю строку складываем с первой и вычитаем из второй строки. Разлагаем по элементам последнего столбца.
= 
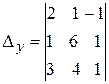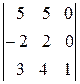=1(-1)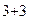 
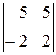=10+10=20.
При вычислении определителя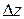 
последнюю строку складываем с первой и со второй строки и разлагаем получившийся определитель по элементам второго столбца.
= 
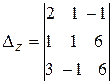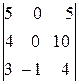=-1(-1)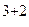 
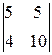=50-20=30.
Подставляя найденные значения в формулы (1.1.1), получим:
х=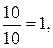 
у= 
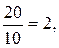z= 
б) Метод Гаусса.
Составим расширенную матрицу системы:
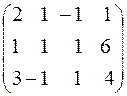
Разрешающим элементом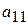 
удобно иметь единицу, поэтому переставим второе уравнение на место первого.
|
|
Получим нули в первом столбце, умножив первое уравнение последовательно на (-2) и (-3) и складывая со вторым и третьим.
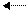
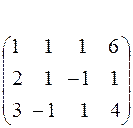(-2) (-3)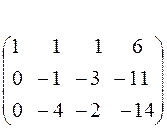 
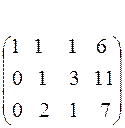
С помощью второго элемента второй строки сделаем нуль во втором столбце третьей строки, для чего умножим вторую строку на (-2) и сложим с третьей.
(-2)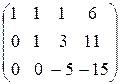 
.
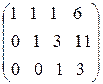Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:
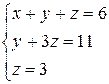
Из последнего уравнения сразу находим значение z=3, подставляя которое во второе уравнение находим у=11-3z=11-9=2. Затем из первого уравнения найдем
х=1, у=2, z=3.
Вопросы для самопроверки
1. Что называется определителем системы?
2. Когда система линейных уравнений имеет единственное решение?
3. Напишите формулы Крамера для решения системы трех линейных уравнений с тремя неизвестными.
4. В чем заключается основная идея метода Гаусса?
5. Какой из рассмотренных методов решения системы линейных уравнений показался Вам более простым?
Аналитическая геометрия на плоскости
Основным методом решения задач аналитической геометрии является метод координат.
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости. Одной из таких систем является прямоугольная (декартова) система координат, которая задается двумя взаимно перпендикулярными прямыми-осями координат, на каждой из которых выбрано положительное направление и масштаб.
Координаты произвольной точки А в системе ОХУ записываются так: А(х;у).
Напомним наиболее важные формулы и уравнения аналитической геометрии, необходимые для решения задач.
|
|
Так, пусть даны две точк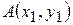и 
и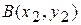 
Тогда: 1)Расстояние между ними определяется по формуле:
. (2.1.1)
2) Координаты точки М (х,у), делящей отрезок АВ в отношении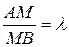 
, имеют вид:
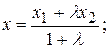
(2.1.2)
3) В частности, координаты середины отрезка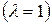 
находятся по формулам:
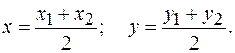(2.1.3)
4) Уравнение прямой, проходящей через две точки, имеет вид:
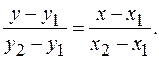(2.1.4)
Уравнение прямой с угловым коэффициентом будет:
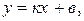(2.1.5)
где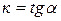 
- угловой коэффициент или тангенс угла, образованного прямой с положительным направлением оси Ох; b – отрезок, отсекаемый прямой на оси Оу.
Угол между двумя прямыми, заданными своими уравнениями с угловыми коэффициентами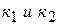 
, находится по формуле:
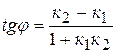. (2.1.6)
Из этой формулы легко получить условие параллельности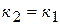 
и перпендикулярности 
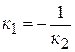прямых.
Во многих задачах используется уравнение прямой, проходящей через данную точку в данном направлении (уравнение пучка прямых):
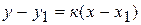, (2.1.7)
где (х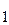 
,у 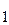) - координаты заданной точки (центр пучка).
Общее уравнение прямой на плоскости имеет вид:
Ах+Ву+С=0. (2.1.8)
Расстояние от точки А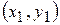 
до прямой, заданной общим уравнением: Ах+Ву+С=0, находится по формуле:
. (2.1.9)
Пример 2.
Найти длину отрезка АВ, если известны координаты точек А(1;1) и В(4;5).
Решение:
Согласно формуле (2.1.1) будем иметь: подставим координаты точек А и В, получим: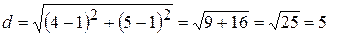 
(ед.дл.).
Пример 3.
Найти уравнение прямой, проходящей через точки А(1;2) и В(4;4) и ее угловой коэффициент.
Решение:
Используем уравнение (2.1.4): Подставим в него координаты точек А и В; 
;
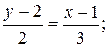
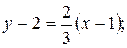
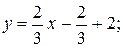
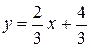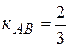- угловой коэффициент.
Пример 4.
Найти уравнение и длину перпендикуляра, опущенного из точки С(1;2) на прямую 3х – 4у + 2 =0.
Решение:
Через точку С проведем пучок прямых(2.1.7):
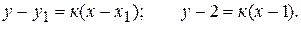
Угловой коэффициент «к» найдем из условия перпендикулярности прямых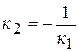 
, для чего прежде найдем угловой коэффициент заданной прямой.
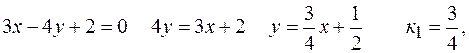тогда 
.
Подставим найденное значение в уравнение пучка прямых.
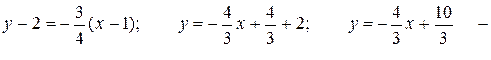уравнение перпендикуляра.
Длину этого перпендикуляра найдем по формуле(2.1.7):
где
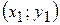- координаты точки С.
В нашем случае это будет: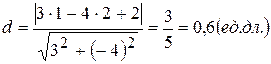 
Пример 5.
Найти: а) уравнение медианы АЕ; б) прямой, проходящей через точку Е, параллельно стороне АВ в треугольнике с вершинами в точках А(-3;0),В(2;5) и С(4;3).
Решение:
а) Найдем координаты точки Е – середины отрезка ВС по формулам(2.1.3):
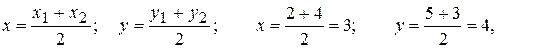Е(3;4).
Уравнение медианы найдем, используя уравнение прямой, проходящей через две точки(2.1.4).
Подставим в него координаты точек А и Е:
.
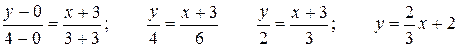б) Прежде, чем ответить на вопрос задачи, найдем уравнение стороны АВ, как прямой, проходящей через две точки. Затем через точку Е проведем пучок прямых, подчинив его условию параллельности прямых.
; 
.
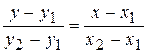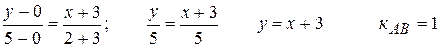Пучок прямых,. проходящих через точку Е: у-4=к (х-3).
Условие параллельности прямых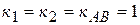 
. Подставим это значение «к» в уравнение пучка, у-4=х-3, или у=х+1.
Вопросы для самопроверки
1. Напишите формулы для вычисления расстояния между двумя точками и деления отрезка в данном отношении.
2. Как найти координаты середины отрезка?
3. Как найти угловой коэффициент прямой, если она задана общим уравнением?
4. Сформулируйте условия параллельности и перпендикулярности прямых.
5. Что представляет собой уравнение пучка прямых?
6. Напишите уравнение прямой, проходящей через две точки.
7. Как найти расстояние от точки до прямой?