Синтез СОО с заданной стоимостью

Синтез СОО с заданным временем ответа (с заданной производительностью)

 

В качестве модели СОО используем разомкнутую стохастическую

сеть.

P₁₁ Допущения:

s₁

p₁₀ 1) поток задач простейший;

2) экспоненциальный закон рас-

v₁ пределения длительности об-

служивания заявок в каждой

s₂ p₁₂ системе сети.

V₂

 

s_n

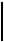
v_n p_1n

 

Рис.18.11.

 

Среднее время пребывания задачи в сети,состоящей из n систем:

 

,

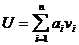где ai - коэффициент передачи (среднее количество обращений к

системе i),

ui -время пребывания заявки в системе i.

В сети могут использоваться типовые устройства ЭВМ, производительность которых заранее известна.

S

v Их стоимость ,

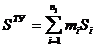где mi -количество i-типовых устройств стоимостью Si.

ni -количество типов ТУ.

 

Нетиповые устройства ЭВМ - у которых производительность может быть различной. Их стоимость:

,

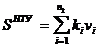где v_i -быстродействие НТУ,

k_i -коэффициент,

n₂-их количество.

Общая стоимость ВС:

;

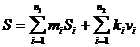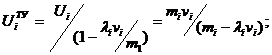
(18.2)

 

К (18.2) применим метод множителей Лагранжа. Составим функцию:

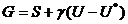, где 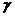-неопределенный множитель.

Дифференцируем G по V_i:

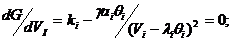, (i=1,...,n₂)

 

Получим:

(18.3)

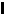
V_imin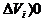

 

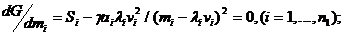
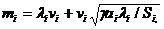(i=1,...,n₁) (18.4)

m_imin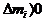

Для нахождения неопределенного множителя 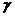используем соотношение, определяющее ограничение на время ответа СОО.ВС будет иметь минимальную стоимость, если U=U*.

В выражение (18.2) подставим (18.3) и (18.4) и получим:

 

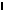
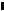
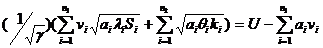
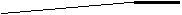можно рассматривать как время пребывания

задачи на типовых устройствах при бесконечном количестве этих

устройств.

 

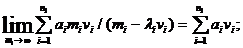
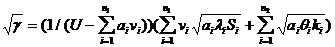(18.5)

Подставляя (18.5) в (18.3), получим vi,которые называются оптимальным распределением быстродействия для СОО с заданным временем ответа.

Распределение быстродействий vi для каждого устройства i заключается в следующем:

1) для каждого устройства выделяется минимально необходимое быстродействие 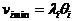(при котором существует стационарный режим);

2) увеличение этого быстродействия за счет минимума затрат до значения, при котором выполниется ограничение на время ответа системы.

Величина добавочного быстродействия для каждого устройства ропорциональна корню нагрузки на устройство и обратно пропорционально ограничению U* на время ответа, т.е. чем меньше время ответа требуется от системы, тем больше величина добавочного быстродействия и, следовательно, стоимость системы:

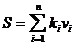(18.6)

где k_i-коэффициент пропорциональности, отражающий стоимость единицы быстродействия.

Стоимость (18.6) минимальна:

1 2

1-определяет минимально допустимую стоимость СОО, при которой обеспечивается стационарный режим в системе без учета ограничений на время ответа;

2-дополнительная стоимость на устройства, при которой выполняется ограничение на время ответа.

 

Синтез СОО с заданной стоимостью

 

1. Производительность (пропускная способность) системы 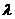ограничена.

2. Суммарная стоимость устройств.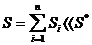

 

3. Оптимальной считается система, имеющая минимальное время ответа U ->min.

Пусть известны характеристики класса задач проектируемой СОО. Определены ресурсы системы: емкость ОП, емкость ВУ, необходимые процессорные операции и операции ввода-вывода в расчете на одну решаемую задачу. На основе этих сведений могут быть определены номенклатура устройств ЭВМ (количество процессоров, каналов ввода-вывода,ВЗУ) и конфигурация связей между ними, т.е. структура ЭВМ.

Теперь возникает задача определения быстродействий устройств: быстродействие процессора (B), времени доступа к ВЗУ. Быстродействие устройств влияет на их стоимость. Быстродействия устройств должны быть согласованы с трудоемкостью задач и стоимость S должна быть распределена между n устройствами. Таким образом, чтобы время ответа U имело минимальное значение.

Задача оптимального распределения стоимости устройств, т.е. их быстродействия при ограничении на суммарную стоимость устройств решается следующим образом.

Модель СОО - разомкнутая стохастическая сеть.

 

P₁₀ Дано:

1) трудоемкости об-

p служивания заявок в каждой из

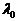
S₁ n систем.

2) a₁,...,a_n -коэффициенты пе-

редач (количество обращений к

p₁₂ соответствующим устройствам

S₂ при решении одной задачи.

3) Допущения: поток простей-

ший,длительности обслуживания

S_n заявок в каждой сети распре-

p_1n делены по экспоненциальному

закону.

Рис.18.12.

 

Сеть экспоненциальна и может рассматриваться как n независимых

систем массового обслуживания с .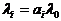

Известны v_i - средняя длительность обслуживания заявок в системе i:

v_i = ;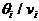

- интенсивность обслуживания.

Время пребывания заявки в системе:

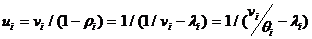
Среднее время пребывания задачи в сети, состоящей из n систем:

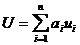, где (18.7)

 

a_i -коэффициент передачи (количество обращений к системе i).

Стоимость системы:

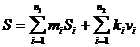(18.8)

Следовательно, задача выбора быстродействий устройств сводится

к минимизации функции (18.7) при ограничении (18.8).

Эта задача решена Л.Клейнроком следующим образом:

к (18.7) применяется метод множителей Лагранжа и составляется

функция G=U+ 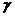(S-S*).

Дифференцируем G по v_i и, приравнивая к нулю, получим:

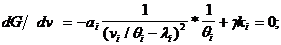
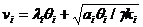(18.9)

 

Дифференцируем G по m _i и приравнивая к нулю, получим:

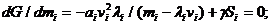
(18.10)

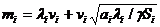
Приравняем S=S*.

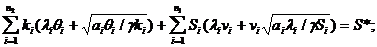
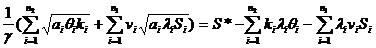
кол-во

нетиповых устройств

S₀

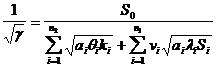(18.11)

Подставляя (5) в (3) получим v_i.

Подставляя (5) в (4) получим m _i.

С учетом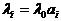

; (18.12)

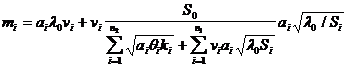; (18.13)

 

Таким образом, минимум среднего времени пребывания задач

(среднего времени ответа на запрос пользователя) для СОО стои-

мостью S достигается при распределении быстродействий v_i в соот-

ветствии с (18.12). Такое распределение быстродействий называется

оптимальным для СОО заданной стоимости. Количество типовых

устройств i-го типа определяется по (18.13).