Лекция № 7
ТЕМА ЛЕКЦИИ
Интервальная оценка случайных составляющих погрешности
Цель лекции – изучить методики определения границ случайных погрешности при наличии различной априорной информации
План лекции:
1. Применение неравенств Чебышева………..………...20 мин.
2. Применение распределения Лапласа………………..20 мин.
3. Применение распределения Стьюдента……………..20 мин.
4. Применение распределения Пирсона………………..20 мин.
Рекомендуемая литература
1. А.Г. Сергеев, М.В. Латышев, В.В. Терегеря. Метрология, стандартизация и сертификация. Стр. 13-37.
2. А.С. Сигов, В.И. Нефедов. Метрология, стандартизация и технические измерения. Стр. 14-41
Вводная часть
В целях повышения психологического настроя студентов на восприятие данной дисциплины в начале каждой лекции целесообразно проводить короткий опрос по материалу предыдущей лекции.
Вопросы для контроля:
а) Что понимается под косвенным измерением?
б) Приведите примеры косвенных измерений.
Требовать от отвечающих студентов представления перед ответом по форме: «Студент Сергеев. Группа ЭП – 1 – 04». Оценки заносить в журнал преподавателя.
После опроса объявить тему и цель лекции.
Основная часть
1. Применение неравенств Чебышева
Более полным и надежным способом оценки случайных величин является интервальная оценка, которая с заданной степенью достоверности включает в себя значение оцениваемого параметра.
При интервальной оценке определяется доверительный интервал ∆1, ∆2, между границами которого с доверительной вероятностью Р находится истинное значение Р[(А - ∆1:) ^ А < (А + ∆2)] = Р =1-q.
Доверительная вероятность определяет область допустимых значений, а уровень значимости — критическую область. Выбираемое значение q должно быть достаточно малым, чтобы не была совершена ошибка первого рода, т. е. чтобы не была забракована правильная оценка. С другой стороны, слишком малое значение q может привести к ошибке второго рода, когда будет принята ложная оценка. Уровень значимости лежит в пределах 0,02 < q < 0,1.
В общем случае доверительные интервалы можно строить на основе неравенства Чебышева, при этом необходимо знать не вид распределения наблюдений, а среднее квадратическое отклонение σх.
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном измерении случайная погрешность по абсолютному значению не превысит некоторого наперед заданного значения ε, т. е. вероятность Р{|∆сл| < ε }. Для этого используется неравенство Чебышева
Р{|∆сл| < ε } > 1 - σх² / ε² или Р{|∆сл| < ε } > σх² / ε².
Однако получаемые с помощью неравенства Чебышева интервалы оказываются слишком широкими, поэтому на практике выясняют вид распределения выборочных характеристик, используемых в качестве оценки выборочной величины, задаются доверительной вероятностью и определяют доверительный интервал. Рассмотрим доверительные интервалы некоторых выборочных распределений.
2. Применение распределения Лапласа
Определение доверительного интервала для выборочного среднего арифметического значения измеряемой величины А при известной дисперсий σх²:
случайная величина (результат измерения) х имеет нормальное распределение с математическим ожиданием тх и дисперсией σх². В этом случае выборочное распределение оценки среднего значения А также нормально и имеет то же математическое ожидание и дисперсию.
Если доверительные границы ∆1 = ∆2 = А2 = z ∙ σх/√n, то доверительный интервал
Р{(А - z ∙ σх/√n) < А < (А + z ∙ σх/√n)},
где z — квантиль нормированного распределения Лапласа;
n – количество измерений.
Значения нормированной функции Лапласа Ф(z) = Р/2
| z | Ф(z) | z | Ф(z) | z | Ф(z) | z | Ф(z) | z | Ф(z) |
| 0,0 0,1 0,2 0,3 0,4 0.5 0,6 0,7 0,8 | 0,00000 0,03983 0,07926 0,11791 0,15542 0,19146 0,22575 0,25804 0,28814 | 0,9 1,0 1,1 1,2 1,3 1.4 1,5 1,6 1,7 | 0,31594 0,34134 0,36433 0,38493 0,40320 0,41924 0,43319 0,44520 0,45543 | 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 | 0,46407 0,47128 0,47725 0,48214 0,48610 0.48928 0,49180 0,49379 0,49534 | 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 | 0,49653 0,49744 0,49813 0,49865 0,49903 0,49931 0,49952 0,49966 0,49977 | 3,6 3,7 3,8 3,9 4,0 4,5 | 0,49984 0,49989 0,49993 0,49995 0,49997 0,49999 |
Результат измерений записывается в форме А ± ∆.
Еслислучайная величина х распределена по закону, отличному от нормального, то и з следствий центральной предельной теоремы вытекает, что при увеличении объема выборки n выборочное распределение среднего значения выборки А приближается к нормальному распределению независимо от вида распределения исходной величины (данное утверждение справедливо, если измеряемая случайная величина обладает конечной дисперсией).
Нормальность выборочного распределения величины А приемлема во многих случаях при п > 4 и вполне хорошо оправдывается при п > 10.
3. Применение распределения Стьюдента
Определение доверительного интервала для выборочного среднего арифметического значения измеряемой величины при неизвестной дисперсии (реальный случай, когда число измерений небольшое). Результаты измерения х распределены по нормальному закону со средним значением тх и неизвестной дисперсией.
Выборочное распределение среднего значения А при неизвестной дисперсии имеет распределение Стьюдента:
Р{[А - tРn* S(А)] <mх<[А + tРn* S (А)]}.
Доверительный интервал определяется через квантиль Стьюдента (см. таблицу) от - tРn* S(А)до + tРn* S(А).
Коэффициенты Стьюдента
| n -1 | P = 0,95 | P = 0,99 | n - 1 | P = 0,95 | P = 0,99 |
| 3,182 2,776 2,571 2,447 2,365 2,306 2,228 2,179 2,145 | 5,841 4,604 4,032 3,707 3,499 3,355 3,169 3,055 2,977 | ∞ | 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,043 1,960 | 2,921 2,878 2,845 2,819 2,797 2,779 2,763 2,750 2,576 |
Этот интервал будет шире и при увеличении числа измерений п приближается к интервалу, рассчитанному через квантиль Лапласа z. В этом случае доверительный интервал будет
А ± tРn* S(А)
где S(А) = √∑(xi – А)²/n(n – 1)
2.4. Применение распределения Пирсона
Определение доверительного интервала для выборочной дисперсии и среднеквадратического отклонения результатов измерений.
Случайная величина х имеет нормальное распределение со средним значением тх и дисперсией σх². Оценка дисперсии выборки объема п независимых значений случайной величины х:
S² = ∑(xi – А)²/(n – 1)
Отношение k* S²/ σх² = χ²
имеет χ² (хи-квадрат) распределение Пирсона с к = п - 1 степенями свободы.
Пользуясь χ² (см. таблицу), можно найти границы доверительного интервала для оценки дисперсии результатов измерений при заданной доверительной вероятности Р =1 - q, где q— уровень значимости.
Квантиль χ² - распределения при различных k,q
| K | 1 – q/2 | q/2 | ||||
| 0,99 | 0,95 | 0,90 | 0,10 | 0,05 | 0,01 | |
| 0,0000157 0,0201 0,115 0,297 0,554 0,872 1,239 1,646 2,088 2,558 3,571 4,660 5,812 7.015 8,260 14,953 | 0,000393 0,103 0,352 0,711 1,145 1,635 2,167 2,733 3,325 3,940 5,226 6,571 7,962 9,390 10,851 18,493 | 0,0158 0,211 0,584 1,064 1,610 2,204 2,833 3,490 4,168 4,865 6,304 7,790 9,312 10,865 12,444 20,599 | 2,706 4,605 6,251 7,779 9,236 10,645 12,017 13,362 14,684 15,987 18,549 21,064 23,542 25,989 28,412 40,256 | 3,841 5,991 7.815 9,488 11,070 12,592 14,067 15,507 16,919 18,307 21,026 23,685 26,296 28,869 31,410 43,773 | 6,635 9,210 11,345 13,277 15,086 16,812 18,475 20,090 21,666 23,309 26,217 29,141 32,000 34,805 37,566 50,892 |
Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q, причем вероятности выхода за обе границы интервала равны между собой и составляют q/ 2, Границы χ²| доверительного интервала находятся как
Р{ χ²k;q/2 < χ² < χ²k;1 – q/2} = 1 - q
Зная границы доверительного интервала для верительный интервал для χ², построим доверительных интервал для дисперсии
Р{(n – 1)S²/ χ²k;q/2 < σх² < (n – 1)S²/ χ²k;1 – q/2} = 1 - q
Полученное выражение означает, что с вероятностью P = 1 - qистинное значение σх² дисперсии результатов измерений лежит в интервале (S1; S2), границы которого
S1 = (n – 1)S²/ χ²k;q/2; S2 = (n – 1)S²/ χ²k;1 – q/2
При обработке результатов измерений случайной величины, заведомо подчиняющейся нормальному закону распределения, при принятии решения об исключении или сохранении резко отклоняющихся (грубых) результатов измерений необходимо внимательно проанализировать условия, в которых получился такой результат. Сомнительным может быть лишь наибольший хмах или наименьший хмш из результатов измерений. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами статистических гипотез. Для проверки гипотезы, что результат не содержит грубой погрешности, вычисляют
утах = (хтах - А)/S или ут!„ = (А - хт{п)/S. Результаты Ушах и Уш1п сравнивают с наибольшим значением уq, которое случайная величина V может принять по чисто случайным причинам. Значения уq для n = 3... 25 протабулированы и представлены в таблице при заданной доверительной вероятности или уровне значимости q.
Значения уq при различных n,q
| n | q | n | q | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||
| 1,406 | 1,412 | 2,326 | 2,493 | ||
| 1,645 | 1,689 | 2,354 | 2,523 | ||
| 1,731 | 1,869 | 2,380 | 2,551 | ||
| 1,894 | 1,996 | 2,404 | 2,557 | ||
| 1,974 | 2,093 | 2,426 | 2,600 | ||
| 2,041 | 2,172 | 2,447 | 2,623 | ||
| 2,097 | 2,237 | 2,467 | 2,644 | ||
| 2,146 | 2,294 | 2,486 | 2,664 | ||
| 2,190 | 2,383 | 2,504 | 2,683 | ||
| 2,229 | 2,387 | 2,520 | 2,701 | ||
| 2,264 | 2,426 | 2,537 | 2,717 | ||
| 2,297 | 2,461 |
Пример расчета границ доверительного интервала. Приближенно определить границы доверительного интервала, в котором с заданной вероятности Р = 0,75 находится истинное значение измеряемой величины. Известно, что sср = 0,2.
Решение. Находим по табл. П5 Прилож. аргумент t функции Ф(t) = =0,75. Значение t = 1,15. Произведение t sср = ±0,23. Следовательно, с вероятностью 0,75 истинное значение находится в интервале ±23% от измеренной величины.
Пример расчета доверительной вероятности. В результате проведения многократных наблюдений напряжения получены следующие результаты в вольтах: 19,2; 18,9; 19,4; 19,1; 18,98; 19,3. Априорно известно, что закон распределения погрешностей нормальный. Определить вероятность, с которой в интервале ± 10 % находится истинное значение измеряемого напряжения.
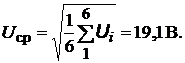Решение. За результат измерения примем
Найдем среднее квадратическое отклонение результата измерения
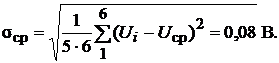
Воспользуемся формулой (6.12):
так как из табл. П6 Прилож. F (1) = 0,818 при количестве наблюдений, равном 6. Таким образом, доверительная вероятность равна 64 %.
Пример расчета границ доверительного интервала. При нормальном законе распределения погрешностей определить интервал, в котором с доверительной вероятностью 95 % находится истинное значение измеряемой физической величины. Среднее квадратическое отклонение результата измерения равно 0,05.
Решение. Преобразуем формулу (6.12) к виду
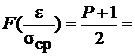
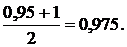
Из табл. П6 Прилож. определим значение аргумента t при значении функции 0,975 и количестве наблюдений, равном 6: t = 2,57. Отсюда e= t sср = = 2,57×0,05 = ± 0,1285.
Заключительная часть
Общие замечания, контроль присутствия
1.
На первой лекции не будет лишним напомнить учащимся о правилах поведения, организационных моментах, связанных с контролем присутствия и периодическим контролем знаний.
Тема лекции дается под запись, цель проговаривается.
Вступительное слово
Ежесекундно при выработке, передаче и потреблении электрической энергии происходят миллионы измерений параметров различных физических объектов. Измерение - сложный процесс, включающий в себя взаимодействие ряда структурных элементов - измерительной задачи, объекта измерения, принципов, методов и средств измерения, его модели, условий измерения, наблюдателя, результата и погрешности измерения. Сам процесс измерения состоит из ряда последовательных этапов, включающих в себя постановку измерительной задачи, планирование измерительного эксперимента, непосредственно измерительный эксперимент, обработку экспериментальных данных, завершаемую анализом и интерпретацией полученных результатов, а также записью результата в соответствии с установленной формой представления. Грамотное и сознательное выполнение всех этапов измерения является залогом сведения к минимуму ошибочных выводов, сделанных по результатам измерений, и принятия решений, не приводящих к материальным и моральным потерям.
Особенно ответственные решения приходится принимать в ряде областей человеческой деятельности, связанных с повышенной опасностью, к которым смело можно отнести и энергетику. Поэтому умение правильно проводить разнообразные измерения для инженера-энергетика трудно переоценить.
Основная часть
1. Цели и задачи дисциплины.
1.1. Определения метрологии, стандартизации и сертификации
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Стандартизация (в соответствии с законом «О техническом регулировании» - это деятельность по установлению правил и характеристик в целях их добровольного многократного использования, направленная на достижение упорядоченности в сферах производства и обращения продукции и повышение конкурентоспособности продукции, работ или услуг.
Сертификация – форма осуществляемого органом по сертификации подтверждения соответствия объектов требованиям технических регламентов, положениям стандартов или условиям договоров.
1.2. Цели, задачи и план прохождения дисциплины.
Дисциплина «Метрология, стандартизация и сертификация» является одной из базовых общепрофессиональных дисциплин, служит общетехнической подготовке студентов и создает теоретическую базу для изучения последующих специальных дисциплин, связанных с контролем, управлением и автоматизацией технологических процессов, производством и передачей электроэнергии, электроснабжением и электрооборудованием соответствующих отраслей.
Цели дисциплины: изучение существующих видов и методов измерений, погрешностей измерений и способов их уменьшения, обработки результатов измерений; получение основных сведений об устройстве и принципе действия различных средств измерений; приобретение определенных навыков практического использования средств измерений и теоретического расчета погрешностей; ознакомление с основами обеспечения единства измерений, целями и задачами стандартизации и сертификации.
Задачи дисциплины:
- знать виды и методы измерений, основы обеспечения единства измерений, причины возникновения, классификацию и способы выражения погрешности измерения, характеристики средств измерений, методику и способы обработки результатов наблюдений, способы повышения точности измерений, методы исключения систематической погрешности;
- знать классификацию средств измерений, характеристики случайных сигналов, принцип действия и свойства средств измерения прямого и уравновешивающего преобразования, содержание терминов: цифровой измерительный прибор, аналоговый измерительный прибор, мера, измерительный преобразователь, квантование по уровню, дискретизация по времени, детерминированный, случайный, стационарный, эргодический сигнал, среднее, средневыпрямленное, действующее значение тока и напряжения, коэффициент формы, коэффициент амплитуды;
- знать цели, задачи и правовые основы стандартизации, виды стандартов, цели и объекты сертификации на международном, региональном и национальном уровнях, схемы и системы сертификации, правила и порядок проведения сертификации;
- иметь представление о государственной системе и международной организации стандартизации, органах по сертификации и испытательных лабораториях, структуре и функциях метрологической службы, обязательной и добровольной сертификации, сертификации услуг и системах качества;
- уметь проводить расчет предельной погрешности, определяемой классом точности средств измерений, погрешности косвенных измерений, методической погрешности, вызванной внутренним сопротивлением электроизмерительного прибора, доверительных интервалов и вероятностей при различных начальных условиях.
План прохождения дисциплины включает:
- лекции - 16 часов;
- практические занятия 16 часов;
-дифференцированный зачет.
2. Физические величины (ФВ) и их единицы
2.1. Общие понятия и определения.
Исходным элементом любого измерения является его цель. Целью измерений является нахождение значений физической величины - оценки ее в принятых единицах с заданной точностью в определенных условиях.
Физическая величина – одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном индивидуальное для каждого из них.
Единица величины - фиксированное значение величины, которое принято за единицу такой величины и применяется для количественного выражения однородных с ней величин;
Внесистемная единица величины - единица величины, не входящая в принятую систему единиц;
Когерентная единица величины - производная единица величины, которая представляет собой произведение основных единиц, возведенных в степень, с коэффициентом пропорциональности, равным 1;
Логарифмическая единица величины - логарифм безразмерного отношения величины к одноименной величине, принимаемой за исходную;
Международная система единиц (СИ) - система единиц, основанная на Международной системе величин.
2.2. Системы единиц ФВ (СИ).
Система единиц величин СИ - совокупность основных и производных единиц СИ, их десятичных кратных и дольных единиц, а также правил их использования;
Основная величина - величина, условно принятая в качестве независимой от других величин Международной системы величин;
Основная единица СИ - единица основной величины в Международной системе единиц (СИ);
Относительная величина - безразмерное отношение величины к одноименной величине, принимаемой за исходную;
Производная величина - величина, определенная через основные величины системы;
Производная единица СИ - единица производной величины Международной системы единиц (СИ);