Функция распределения вероятностей и ее свойства. Независимость случайных величин; критерий их независимости.
Для одномерной С.В. Х.
Функция распределения – числовая функция F(x), определенная на всей числовой прямой и принимающая значение: F(x)=P(X<x). Свойства
1. F( )=
)= 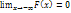 , F(+
, F(+  )=
)= 
F( )=P(X<
)=P(X<  )=P(
)=P( )=0
)=0
F(+  )=P(X<+
)=P(X<+  )=P(Ω)=1
)=P(Ω)=1
2. F(x) неубывает по x, т.е. для  ,F(
,F( )
) 
P( )=P(X<
)=P(X<  )=P({X<
)=P({X<  }+{
}+{  })=P(X<
})=P(X<  )+P(
)+P( )=F(
)=F( )+P(
)+P( ), F(
), F( )
)  .
.
3. 0  (из св-в 1 и 2.)
(из св-в 1 и 2.)
4. F(x) непрерывна слева по x, т.е.  или
или  где
где  ,
,
 =F(
=F( )+P(
)+P( ), тогда F(
), тогда F( )= P(
)= P( ),
),

5. P(X 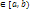 )=P(a
)=P(a  )=F(b)-F(a)-осн. Ф-ла вероятностей СВ.
)=F(b)-F(a)-осн. Ф-ла вероятностей СВ.
{X<b}={a  }+{X<a}, P(X<b)=P(a
}+{X<a}, P(X<b)=P(a  )+P(X<a)
)+P(X<a)
F(b)=P(a  )+F(a), F(b)-F(a)=P(a
)+F(a), F(b)-F(a)=P(a  ).
).
Из св-в 1,2,4  что каждая ф-я распределения явл. Неубыв. Слева, уд.усл: F(
что каждая ф-я распределения явл. Неубыв. Слева, уд.усл: F( )=0, F(+
)=0, F(+  )=1. Верным является и обратное:всякая ф-я, удовл. этим условиям может рассматриваться как ф-я распределения нек. СВ. Эти св-ва явл. Характеристич. Для ф-ии распред СВ.
)=1. Верным является и обратное:всякая ф-я, удовл. этим условиям может рассматриваться как ф-я распределения нек. СВ. Эти св-ва явл. Характеристич. Для ф-ии распред СВ.
Ф-я распред. n-мерной СВ ( ) определяется ан-но, т.е. ф-я распред n-мерной СВ F(
) определяется ан-но, т.е. ф-я распред n-мерной СВ F( ) нзв числовую ф-ю, определенную в n-мерном арифмет пр-ве
) нзв числовую ф-ю, определенную в n-мерном арифмет пр-ве  , знач-е которой опред-ся рав-ом: F(
, знач-е которой опред-ся рав-ом: F( )=P(
)=P(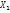 <
< 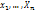 <
<  )
)
P({ 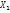 <
< 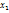 }...{
}...{ 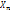 <
<  }).
}).
С геом точки зрения: F( вероятность попадания значения (-
вероятность попадания значения (- 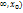
Ф -и распред многомерн СВ обладают св-ми(н-р для ф-ии распред двумерн СВ):
1. 0 
2. F(x,y)-неуб по каждому из аргументов
3. F(x,y) – непрер слева по каждому их аргументов
4. F(+  )=
)=  ,
, 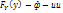 распред составляющей сногомерн СВ, эти законы иногда нзв предельными законами.
распред составляющей сногомерн СВ, эти законы иногда нзв предельными законами.
Понятие независимости СВ опред след образом: 2 СВ X,Y нзв независимыми, ес вып рав-ва: F(x,y)=  ес СВ X,Y- дискрет СВ критерий их независимости формулир-ся след образом: Они будут независимы тогда и только тогда когда вы прав-во:
ес СВ X,Y- дискрет СВ критерий их независимости формулир-ся след образом: Они будут независимы тогда и только тогда когда вы прав-во: 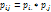 для
для  где
где 
 ЕсX непрер СВ крит их независимости формул след образ: они независ тогда и токо тогда когда ф-я плотности распред вер-ти: f(x,y)=
ЕсX непрер СВ крит их независимости формул след образ: они независ тогда и токо тогда когда ф-я плотности распред вер-ти: f(x,y)= 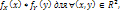
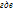 f(x,y)=
f(x,y)=  -совместная ф-я плотности распред вер-ти;
-совместная ф-я плотности распред вер-ти; 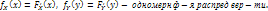
Закон больших чисел Чебышева. Центральная предельная теорема для сумм независимых одинаково распределенных случайных величин.
Под законом больших чисел в ТВ понимают ряд предельных теорем в кажд из которых устанавливают факт сходимости средних арифметич большого числа СВ к некот неслучайным величинам. Основной формой закона больших чисел явл предельная теор Чебышева.
Теорема Чебышева (Закон больших чисел в форме Чебышева)
Пусть X1,X2,…,Xn, - послед-ть независимых случ. величин с матем ожиданием и дисперсиями: MXi=ai; DXi=  , (ограниченными одним и тем же числом c)
, (ограниченными одним и тем же числом c)
Тогда для ε  имеет место равенство:
имеет место равенство:
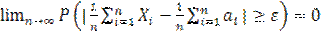 или
или 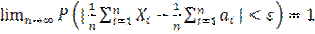 .
.
Т о в теор Чебышева утверж-ся,что сред аоиф СВ при большом числе слагаемых теряет св-во случайности и может быть заменено неслуч величиной средним арифм их мат ожиданий.
Следствие: Если послед-ть X1, X2,…,Xn,… - послед-ть независ. одинаково-распределенных случ величин с мат ожиданием MXi=a, DXi=  ,тогда для
,тогда для 
 , если a – измеряемое зн-е некот величины, точное зн-е которого неизвестно.Найти приблизит. зн-ие можно выбирая среднее арифметич всех результатов.
, если a – измеряемое зн-е некот величины, точное зн-е которого неизвестно.Найти приблизит. зн-ие можно выбирая среднее арифметич всех результатов.
В основе док-ва теор Чебышева лежит нер-во Чебышева и понятие сх-ти послед-ти СВ по вероятности. Посл-ть СВ X1, X2,…, Xn,…нзв сх-ся по вероятности к нек величине A, ЕС для 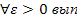 рав-во:
рав-во: 
Сх-ть по вероятности означает, что послед-ть СВ X1, X2,…, Xn,… приближается к величине А (она м б случайной и неслучайной), так что отклонение  от A по модулю, превосходящее
от A по модулю, превосходящее  становятся все менее вероятнее с увеличением n но отклонения <
становятся все менее вероятнее с увеличением n но отклонения <  становятся все более достоверными.
становятся все более достоверными. 
Для кажд СВ X имеющей конечную дисперсию DX при 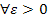 им место нер-во:
им место нер-во:
P( )
) 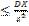 – нер-во Чебышева.
– нер-во Чебышева.
Д-во теор Чебышева: П/ь Yn= 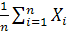 ; MYn=M(
; MYn=M(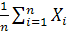 )=
)=  ;
;
DYn=D(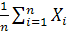 ) =
) =  , согласно 2-му неравенству Чебышева (П/ь X- случ величина, обладающая конечной дисперсией
, согласно 2-му неравенству Чебышева (П/ь X- случ величина, обладающая конечной дисперсией  , тогда для ∀ε
, тогда для ∀ε 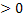 имеет место нер-во:
имеет место нер-во: 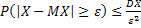 )) вероятность
)) вероятность  ;
;
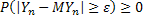 ;
; 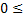
 след-но
след-но 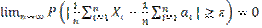 ч.т.д.
ч.т.д.
В центр пред теореме исследуется вопрос возникновения нормального распределения как предельного для суммы большого числа СВ. Она выявляет ту особую роль, кот играет норм распр-е. На практике норм закон всегда им место в тех случаях кгд СВ является результатом действ на большого числа равномерно малых но их влиянию на весь результатслуч факторов действующихнезависимо др от друга
Для случая одинаково распред-х предельн независ СВ
Цкетральная пред теор формул след обр: П/ь X1, X2,…,Xn,… - послед-ть независ. одинаково-распределенных случ величин с мат ожиданием MXi=a, DXi=  , тогда ф-я распред стандартизированной СВ
, тогда ф-я распред стандартизированной СВ  для
для  стремится к ф-ии распределения стандартной нормальной СВ.
стремится к ф-ии распределения стандартной нормальной СВ.

 , т.е.
, т.е. 