Лекция 6
Предел последовательности
Напомним обозначения двух логических символов, символ  - знак всеобщности; символ
- знак всеобщности; символ  - символ существования.
- символ существования.
Обозначим через N множество натуральных чисел. Итак, N=  .
.
Определение 1. Последовательностью действительных чисел  называется закон, согласно которому каждому
называется закон, согласно которому каждому  N ставится в соответствие действительное число
N ставится в соответствие действительное число  , называемое элементом последовательности. Элемент
, называемое элементом последовательности. Элемент  называется общим членом последовательности.
называется общим членом последовательности.
Определение 2. 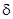 - окрестностью точки - окрестностью точки  называется множество точек называется множество точек  , удовлетворяющих неравенству , удовлетворяющих неравенству  (которое равносильно двойному неравенству (которое равносильно двойному неравенству  ). ).
|
Геометрически 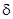 - окрестность точки
- окрестность точки  представляет собой открытый интервал
представляет собой открытый интервал  числовой прямой:
числовой прямой:

Определение 3. 1) Число  называется пределом последовательности
называется пределом последовательности  , если
, если  (N – натуральное число), такое, что
(N – натуральное число), такое, что  число
число  попадает в
попадает в 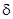 - окрестность точки a, то есть выполняется неравенство:
- окрестность точки a, то есть выполняется неравенство:
 . .
|
Тот факт, что a есть предел  обозначается следующим образом:
обозначается следующим образом:  .
.
2) В случае, если не существует числа  , удовлетворяющего пункту 1) данного определения, говорят что последовательность
, удовлетворяющего пункту 1) данного определения, говорят что последовательность  расходится (не имеет конечного предела).
расходится (не имеет конечного предела).
3) Если  ,
, 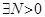 , такое, что
, такое, что 
 (соответственно,
(соответственно,  ), то говорят, что последовательность
), то говорят, что последовательность  расходится к
расходится к 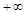 (соответственно, расходится к
(соответственно, расходится к  ), и этот факт обозначают следующим образом:
), и этот факт обозначают следующим образом:  (соответственно,
(соответственно,  ).
).
4) Если  ,
, 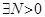 , такое, что
, такое, что 
 , то говорят, что последовательность
, то говорят, что последовательность  расходится к
расходится к  , и этот факт обозначают следующим образом:
, и этот факт обозначают следующим образом: 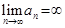 .
.
Определение 4. Последовательность  называется монотонно возрастающей (соответственно, монотонно убывающей), если
называется монотонно возрастающей (соответственно, монотонно убывающей), если  N
N  (соответственно,
(соответственно,  ). Если
). Если  N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности.
N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности.
Определение 5. Число  называется числом Эйлера.
называется числом Эйлера.
Определение предела функции
Рассмотрим действительную функцию 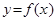 действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть
действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть  или просто
или просто  ).
).
Определение 6. 1) Предположим, что существует хотя бы одна последовательность  D(y), строго стремящаяся к a. Точка b называется пределом функции
D(y), строго стремящаяся к a. Точка b называется пределом функции 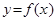 при x стремящемся к a, если для любой последовательности
при x стремящемся к a, если для любой последовательности  D(y), строго стремящейся к a, выполняется соотношение:
D(y), строго стремящейся к a, выполняется соотношение:  . Тот факт, что b является пределом функции
. Тот факт, что b является пределом функции 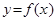 при х стремящемся к a, обозначают так:
при х стремящемся к a, обозначают так:  .
.
2) Предположим, что существует хотя бы одна последовательность  D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции
D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции 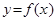 при x стремящемся к a, если для любой последовательности
при x стремящемся к a, если для любой последовательности  D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение:
D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение:  . Обозначение левого предела:
. Обозначение левого предела:  (соответственно, правого предела:
(соответственно, правого предела:  ).
).
Теорема. Если  , то
, то  .
.
Свойства предела функции
1. Если  то
то  .
.
2. Если 
 и
и 
 и конечны, то
и конечны, то 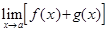 =
=  +
+  .
.
3. Если  и
и 
 и конечен, то
и конечен, то 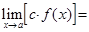
 .
.
4. Если 
 и
и 
 и конечны, то
и конечны, то 
 .
.
5. Если 
 и
и 
 и конечны и, то
и конечны и, то  .
.
6. Если в некоторой окрестности точки a (исключая, быть может, саму a)  и
и 
 и
и 
 , то
, то 
 .
.
7. Если  =
=  = b и если в некоторой окрестности точки a (исключая, быть может, саму a)
= b и если в некоторой окрестности точки a (исключая, быть может, саму a) 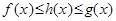 то
то 
 .
.
8. Если в некоторой окрестности точки a (исключая, быть может, саму a) функция 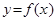 ограничена, а
ограничена, а  , то
, то  .
.
Замечательные пределы
1.  (первый замечательный предел).
(первый замечательный предел).
2.  (второй замечательный предел).
(второй замечательный предел).