Задача 1.
СМО
Номер варианта – последняя цифра зачетной книжки.
1. Дежурный по администрации города имеет 5 телефонов. Телефонные звонки поступают с интенсивностью 90 заявок в час. Средняя продолжительность разговора составляет 2мин.
Определить показатели дежурного администратора как объекта СМО.
2. На стоянке автомобилей возле магазина имеются 3 места, каждое из которых отводится под один автомобиль. Автомобили прибывают на стоянку с интенсивностью 20 автомобилей в час. Продолжительность пребывания автомобилей на стоянке составляет в среднем 15 мин. Стоянка на проезжей части не разрешается.
Определить среднее количество мест, не занятых автомобилями, и вероятность того, что прибывший автомобиль не найдет на стоянке свободного места.
3. АТС предприятия обеспечивает не более 5 переговоров, одновременно. Средняя продолжительность разговоров составляет 1 мин. На станцию поступает в среднем 10 вызовов в секунду.
Определить характеристики АТС как объекта СМО.
4. В морской порт поступает в среднем 6 сухогрузов в сутки. В порту имеются 3 крана, каждый из которых обслуживает 1 сухогруз в среднем за 8 часов. Краны работают круглосуточно.
Определить характеристики работы порта как объекта СМО и в случае необходимости дать рекомендации по его улучшению его работы.
5. В магазине покупателей обслуживают 2 продавца. Среднее время обслуживания одного покупателя – 4 мин. Интенсивность потока покупателей – 3 человека в минуту. Вместимость магазина такова, что одновременно в нем в очереди могут находиться не более 5 человек. Покупатель, пришедший в переполненный магазин, когда в очереди уже стоит 5 человек, не ждет снаружи и уходит.
|
|
Определить вероятность того, что пришедший в магазин покупатель покинет магазин необслуженным.
6. Морской вокзал г. Североморск обслуживает касса с двумя окнами. В выходные дни, когда население активно морским сообщением, интенсивность потока сообщений составляет 0,9 человек/мин. Кассир затрачивает на обслуживание пассажира в среднем 2 мин.
Определить среднее число пассажиров у кассы и среднее время, затрачиваемое пассажиром на приобретение билета.
7. На АЗС имеются 3 колонки. Площадка при станции, на которой машины ожидают заправку, может вместить не более одной машины, и если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а проезжает на соседнюю АЗС. В среднем машины прибывают на станцию каждые 2 мин. Процесс заправки одной машины продолжается в среднем 2,5 мин.
Определить вероятность отказа, абсолютную пропускную способность АЗС, среднее число машин, ожидающих заправку, среднее время ожидания машины в очереди, среднее время пребывания машины на АЗС (включая обслуживание).
8. Салон – парикмахерская имеет 4 мастера. Входящий поток посетителей имеет 5 человек в час. Среднее время обслуживания одного клиента составляет 40 мин.
Определить среднюю очередь на обслуживание, считая ее неограниченной.
9. В мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской, не ожидая. Среднее число клиентов, обращающихся в мастерскую за 1 час, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин.
|
|
Определить вероятность того, что клиент получит отказ, будет обслужен, а также среднее число клиентов, обслуживаемых мастерской в течении 1 часа, и среднее число занятых мастеров.
10. В мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской. Среднее число клиентов, обращающихся в мастерскую за 1 час, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин. Определить вероятность того, что клиент получит отказ, будет обслужен, а также среднее число клиентов, обслуживаемых мастерской в течении 1 часа, и среднее число занятых мастеров.
Задача 2
Анализ поведения потребителя при известной функции полезности
Пусть предпочтения потребителя, покупающего два блага, описываются следующей функцией полезности:
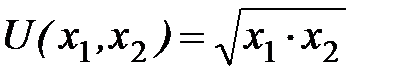 ,
,
где х 1 и х 2 – объемы потребления первого и второго блага соответственно.
Требуется:
1. Определить цены на первое и второе благо (Р1 и Р2) при следующих условиях: доход потребителя составляет I; известно, что при сложившихся ценах, затрачивая весь свой доход, потребитель может купить один из двух следующих наборов благ: набор 1 или набор 2.
2. Сформулировать модель поведения потребителя. Найти оптимальный объем потребления (х*1 и х*2) и предельную полезность денег.
Исходные данные
| № | набор 1 | набор 2 | I |
| (14, 15) | (9, 16) | ||
| (14, 19) | (13, 21) | ||
| (14, 18) | (10, 21) | ||
| (12, 19) | (7, 23) | ||
| (13, 16) | (12, 18) | ||
| (14, 18) | (11, 23) | ||
| (11, 19) | (8, 21) | ||
| (10, 17) | (7, 20) | ||
| (11, 15) | (9, 17) | ||
| (12, 17) | (11, 20) |
|
|
Задача 3
Сетевое планирование
Дан перечень работ и время выполнения каждой работы.
Требуется:
1. построить сетевой график;
2. найти временные параметры сетевого графика;
3. определить, сколько всего времени понадобится для выполнения всех работ;
| Параметр | Номер варианта | |||||||||
| 0-1 | ||||||||||
| 1-2 | ||||||||||
| 1-3 | ||||||||||
| 2-4 | ||||||||||
| 2-6 | ||||||||||
| 3-5 | ||||||||||
| 3-6 | ||||||||||
| 4-5 | ||||||||||
| 5-6 | ||||||||||
| 6-7 | ||||||||||
| 7-8 |