Самостоятельная работа
Тема: «Исследование функции с помощью производной (по графику производной)».
Цель работы: выработать специфические умения и навыки по работе с графиком производной функции для их применения при выполнении практической работы; формирование умений читать свойства функции по графику её производной; умений анализировать материал, выявлять аналогии; способствовать формированию мышления, направленного на решение нестандартных задач;
Умение и навыки, которые должны приобрести студенты: самостоятельное овладение навыками чтения свойств функций по графикам их производных, осуществлять поиск информации с использованием компьютерной техники и Интернета.
Рекомендации по выполнению.
1. По данным, приведённым в таблице, охарактеризуйте поведение функции.
2. Построить графики функций и их производных в одной системе координат.
3.Для графиков функции заполнить таблицу по схеме.
4.По построенным графикам производных исследовать свойства функции. Заполнить третий столбец таблиц. Сравнить с правильным заполнением таблиц. Сделать вывод.
5.Выполнить задания тренажера.
6.Оформить решение задач тренажера в тетради.
1.По следующим данным, приведённым в таблице, охарактеризуйте поведение функции.
| х | (-3;0) | (0;4) | (4;8) | (8;+∞) | |||
| f΄(x) | + | - | - | + | |||
| f(x) | -3 | -5 |
Запишите вывод.
2.Построить графики функций и их производных в одной системе координат:
- у=x2+4x+3 и y΄=2x+4;(нечетный номер в журнале)
- у=3x5-5x3+1 и у΄=15x4-15x2.(четный номер в журнале).
Проверить правильность построения графиков (Приложение 1)
3.Для графика функции заполнить таблицу по схеме исследования свойств функции:
- D(y);
- E(y);
- является ли функция чётной (нечётной);
- нули функции;
- промежутки знакопостоянства;
- промежутки монотонности;
- точки экстремума, экстремумы функции
- наибольшее и наименьшее значения функции.
4.По построенным графикам производных исследовать свойства функции. Заполнить третий столбец таблиц. Сравнить с правильным заполнением таблиц (Приложение 1).
4.1.Для функции у =x2+4x+3 и ее производной.
| у =x2+4x+3 | у =2x+4 | |
| D(y) | R | |
| E(y) | [-1;+∞) | |
| нули функции | x=-3;-1 | |
| чётность (нечётность) | ни четная ни нечётная | |
| промежутки знакопостоянства | y>0 на (-∞;-3) и (1;+∞); y<0 на (-3;-1) | |
| промежутки возрастания – убывания – | [-2;+∞) (-∞; -2] | |
| точки экстремума и значения функции в этих точках | x =-2 – точка минимума, y(-2)= -1 – наименьшее значение | |
| наибольшее и наименьшее значения функции | у=-1 – наименьшее значение, наибольшего значения нет |
4.2.Для функции у=3x5-5x3+1 и ее производной.
| у=3x5-5x3+1 | у=15x4-15x2 | |
| D(y) | R | |
| E(y) | R | |
| количество нулей функции | ||
| чётность (нечётность) | ни чётная ни нечётная | |
| количество промежутков знакопостоянства | y>0 – 2 y<0 – 2 | |
| Промежутки возрастания – убывания – | (-∞;-1], [1;+∞) [-1;1] | |
| точки экстремума и значения функции в этих точках | х=-1 – точка максимума, х=1 – точка минимума, у(-1)=3, у(1)=-1 | |
| наибольшее и наименьшее значения функции | Нет |
4.3.Сделать вывод: по графику производной функции мы можем указать …..
5.Выполнить задания тренажера
Тренажер «Исследование функцию
с помощью производной (по графику производной)»
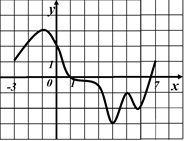По графику производной ответить на вопросы:
1) Функция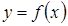 
определена
на промежутке (– 3; 7). На рисунке
изображен график ее производной.
Найдите точку,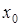 
в которой
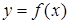принимает наибольшее значение.
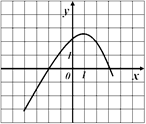2) На рисунке изображен график производной 
Найдите точку максимума функции
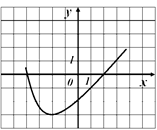3) На рисунке изображен график производной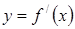
Найдите точку минимума функции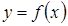
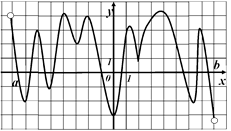4) Функции 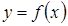задана на отрезке 
.
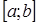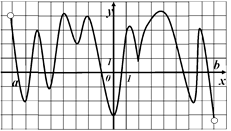
На рисунке изображен график ее производной
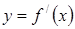. Исследуйте функцию 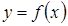на
монотонность ив ответе укажите длину
промежутка убывания
5) Функции 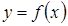задана на отрезке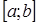
На рисунке изображен график ее производной
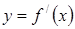Исследуйте на экстремумы функцию 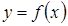. В ответе укажите количество точек минимума.
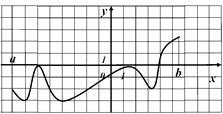
6) Функции 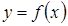задана на отрезке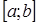
На рисунке изображен график ее производной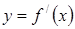
Исследуйте на экстремумы функцию 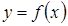. В ответе укажите количествоточек максимума.