Лекция 1
МеТоды оптимизации
Метод наименьших квадратов
Решение переопределенной системы линейных уравнений методом наименьших квадратов
Рассмотрим переопределенную систему линейных уравнений
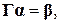 (1.1.1)
(1.1.1)
где Γ ― матрица размерности r × s, причем r > s, α и β ― векторы соответствующей размерности.
Задача приближенного решения такой системы в смысле наименьших квадратов будет иметь вид
 (1.1.2)
(1.1.2)
Сформулируем необходимое условие экстремума
 (1.1.3)
(1.1.3)
Отсюда
 (1.1.4)
(1.1.4)
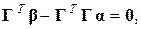 (1.1.5)
(1.1.5)
 (1.1.6)
(1.1.6)
Приближенное оценивание элементов матриц динамической линейной модели методом наименьших квадратов
Нелинейная динамическая модель объекта управления, имеет вид [1]
 (1.2.1)
(1.2.1)
где x p ― вектор состояния, u p ― вектор управления, w p ― вектор внешних воздействий, а f ― нелинейная вещественная векторная функция. Координаты вектора состояния (переменные состояния) такого объекта управления, например авиационного газотурбинного двигателя (ГТД), это частоты вращения роторов, температуры и давления в различных сечениях проточной части двигателя. Координаты вектора управления (переменные управления) ― это расход топлива, изменяемые геометрические характеристики проточной части двигателя, в частности, площадь критического сечения реактивного сопла и углы поворота направляющих аппаратов вентилятора и компрессора. Координаты вектора внешних воздействий (переменные внешних воздействий) это угол отклонения рычага управления двигателем (управляющее воздействие), а также высота и скорость полета (переменные внешних условий).
Соответственно, нелинейная статическая модель объекта управления, имеет вид
 (1.2.2)
(1.2.2)
Постоянные управляющее воздействие и внешние условия, входящие в вектор s w p, определяют установившийся режим работы двигателя (рабочую точку), которому соответствуют вектор установившихся значений переменных управления s u p и вектор установившихся значений переменных состояния s x p.
В небольшой окрестности произвольного установившегося режима нелинейный объект управления можно приближенно описать [1] с помощью линейной динамической модели в нормированных отклонениях от установившихся значений
 (1.2.3)
(1.2.3)
или
 (1.2.4)
(1.2.4)
где
 (1.2.5)
(1.2.5)
 (1.2.6)
(1.2.6)
A и B ― матрицы динамической линейной модели для рассматриваемого установившегося режима.
Для оценивания матричных параметров динамической линейной модели используются переходные процессы нелинейной модели объекта управления в отклонениях от установившихся значений  . При этом переходный процесс
. При этом переходный процесс  состоит из разнесенных по времени прямоугольных импульсов по каждой из координат вектора управления. Здесь
состоит из разнесенных по времени прямоугольных импульсов по каждой из координат вектора управления. Здесь  соответствуют
соответствуют  , причем
, причем  , где
, где  это шаг дискретности.
это шаг дискретности.
Если шаг дискретности достаточно мал, то можно приближенно считать, что произвольная строка векторно-матричного описания линейной модели в отклонениях (1.2.4) имеет вид

 (1.2.7)
(1.2.7)
Пусть
 (1.2.8)
(1.2.8)
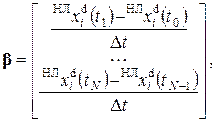 (1.2.9)
(1.2.9)
 (1.2.10)
(1.2.10)
где r = N, s = n+m.
Таким образом, можно приближенно оценивать элементы матриц динамической линейной модели с помощью метода наименьших квадратов (1.1.6).
Пример 1.2.1 Оценивание параметров линейной модели с постоянными коэффициентами методом наименьших квадратов
Пусть линейная модель имеет вид

Рассмотрим реакцию этой модели на единичное ступенчатое воздействие при нулевых начальных условиях, если a = –1, b = 1.
| t | u | x |
| 0.1 | 0.096 | |
| 0.2 | 0.183 | |
| 0.3 | 0.262 | |
| 0.5 | 0.397 | |
| 0.637 | ||
| 1.5 | 0.781 | |
| 0.868 | ||
| 2.5 | 0.920 | |
| 0.952 |
Задачу оценивания коэффициентов a и b можно свести к задаче (1.1.2).


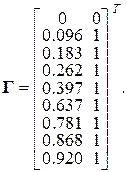
В этом случае применение (1.1.6) дает оценку
 .
.