Лекция 3
МеТоды оптимизации
Нейронные сети
Модель нейрона и нейронная сеть
Модель нейрона представлена на рис.1.1.
Здесь
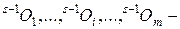разные входы одного нейрона s-ого слоя,
веса связей разных входов нейрона s-ого слоя,
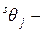сигнал смещения для данного нейрона s-ого слоя,
функция активации данного нейрона s-ого слоя,
одинаковые выходы данного нейрона s-ого слоя,
(1.1.1)
где
(1.1.2)
или
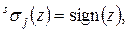(1.1.3)
или
(1.1.4)
Сигмоидная функция активации изображена на рис.1.2.
Рис.1.1 Модель нейрона.
Рис.1.2 Сигмоидная функция активации.
Рис.1.3 Нейронная сеть.
На рис.1.3 изображена простейшая нейронная сеть, которая включает в себя m нейронов входного слоя с линейной функцией активации (1.1.2), n нейронов скрытого (промежуточного) слоя (в общем случае скрытых слоев может быть несколько) с нелинейными функциями активации (1.1.4) и l нейронов выходного слоя с линейной функцией активации (1.1.2).
У каждого из нейронов входного слоя по одному входу, а у каждого из нейронов выходного слоя по одному выходу. У каждого из нейронов входного слоя n одинаковых выходов, а у каждого из нейронов скрытого слоя l одинаковых выходов. Соответственно, на входе у каждого из нейронов скрытого слоя выходы всех нейронов входного слоя, а на входе у каждого из нейронов выходного слоя выходы всех нейронов скрытого слоя.
Управление системой с помощью линейного регулятора, дополненного нелинейной нейронной сетью
Пусть в дискретные моменты времени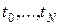 
описание линейного регулятора, дополненного параллельной нелинейной нейронной сетью, вместе с уравнением замыкания имеет вид
(1.2.1)
Здесь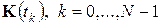 
матрица коэффициентов линейного регулятора, а 
это дополнительный вектор управления, который формируется параллельной линейному регулятору нелинейной нейронной сетью. Этот дополнительный вектор используется для того, чтобы приблизить значения переменных состояния замкнутой системы управления к заданным значениям. Применение нейронной сети для формирования дополнительного вектора управления соответствует решению задачи нелинейного программирования без ограничений градиентным методом. При этом для одномерного поиска используются уравнения линейной модели объекта управления и метод золотого сечения.
Целевая функция нейронной сети управления в каждый момент времени 
представляет собой квадратичную функцию ошибок и затрат вида
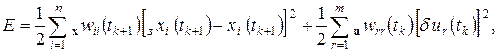(1.2.2)
где 
и 
положительные элементы соответствующих диагональных весовых матриц.
Входные сигналы нейронной сети управления
(1.2.3)
а выходные сигналы этой нейронной сети
(1.2.4)
Тогда
― входы и равные им выходы n нейронов входного слоя (у каждого из нейронов входного слоя по одному входу и q одинаковых выходов для каждого из нейронов скрытого слоя),
― веса связей разных входов q нейронов скрытого слоя,
― выходы q нейронов скрытого слоя (у каждого из q нейронов скрытого слоя m одинаковых выходов), каждый из которых равен 
, 
, 
, 
сигналы смещения скрытого слоя, 
,
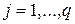― веса связей разных входов m нейронов выходного слоя,
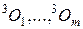― m выходов нейронов выходного слоя (у каждого из нейронов выходного слоя по одному выходу), каждый из которых равен 
, 
сигналы смещения выходного слоя, 
.
Определим компоненты вектора градиента, соответствующего алгоритму обучения (“алгоритму обратного распространения”), то есть алгоритму выбора весов связей скрытого и выходного слоев нейронной сети управления с помощью метода наискорейшего спуска. Объединим все переменные, которые подбираются в процессе обучения, в один вектор
(1.2.5)
размерность которого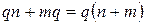 
.
Поскольку в каждый момент времени при известном входном сигнале 
, 
выходной сигнал нейронной сети 
, 
, то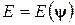 
.
Тогда один шаг оптимизации (минимизации) в направлении, противоположном направлению вектора градиента 
(в направлении “наискорейшего спуска”), будет иметь вид
(1.2.6)
где величина шага 
определяется с помощью минимизации функции одной переменной
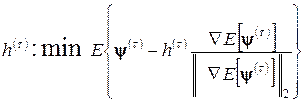(1.2.7)
одним из методов одномерного поиска, например, методом золотого сечения.
Компоненты вектора градиента определим аналитически.
(1.2.8)
(1.2.9)
Поскольку
(1.2.10)
(1.2.11)
то
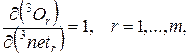(1.2.12)
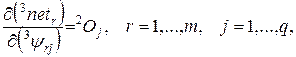(1.2.13)
(1.2.14)
(1.2.15)
(1.2.16)
Здесь 
веса связей выходного и скрытого слоев, 
сигналы смещения выходного слоя, 
выходные сигналы и сигналы смещения скрытого слоя.
Согласно теореме о дифференцировании сложной функции многих переменных
(1.2.17)
В данном выражении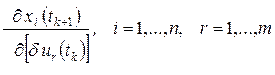 
можно определить с помощью уравнения линейной модели объекта управления
(1.2.18)
Таким образом, в силу (1.2.8, 1.2.12, 1.2.13)
(1.2.19)
где (1.2.17, 1.2.18)
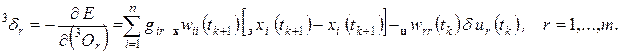(1.2.20)
Соответственно, в силу (1.2.9, 1.2.12, 1.2.14, 1.2.15, 1.2.16, 1.2.20)
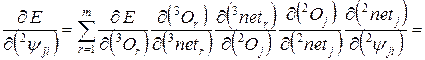
(1.2.21)
где
(1.2.22)