| Элемент | |||||||||
| Надёжность | 0.5 | 0.6 | 0.3 | 0.6 | 0.8 | 0.2 | 0.4 | 0.3 | 0.3 |
Основная схема
Резервная схема
Расчеты по пунктам задания
Раздельное резервирование обеспечивает возможность включения очередного резервного элемента при отказе любого элемента основной цепи.
Сначала вычислим надёжность основной схемы.
При вычислении, имеем ввиду, что надёжность последовательно соединённых элементов A и B равна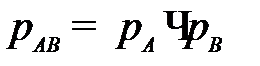 
. Надёжность же параллельно соединённых элементов равна 
.
Надёжность основной цепи
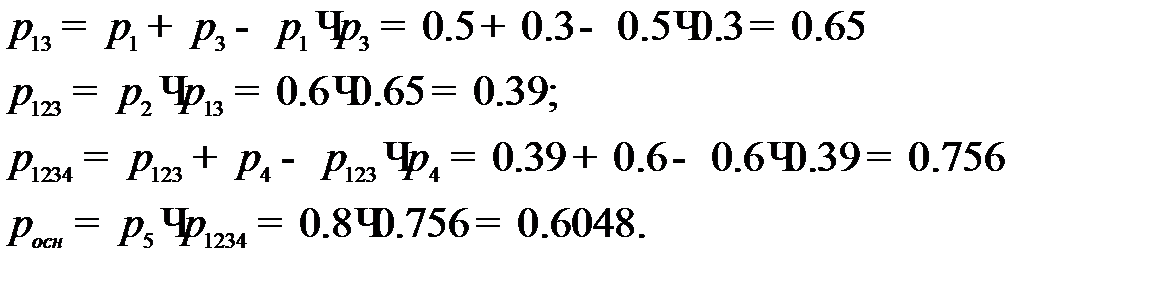
Надёжность меньше 0,95.
Проведём резервирование. Добавим к каждому элементу основной цепи
элемент половинной надёжности.
Схема резервирования
Рассчитаем надёжность резервированного элемента 
.
| Элемент | |||||
| Надёжность | 0.5 | 0.6 | 0.3 | 0.6 | 0.8 |
| Надёжность резервирующего элемента | 0,25 | 0,3 | 0,15 | 0,3 | 0,4 |
| Надёжность резервированного элемента | 0.6250 | 0.7200 | 0.4050 | 0.7200 | 0.8800 |
Рассчитываем надёжность цепи после однократного резервирования, используя надёжности из таблицы.
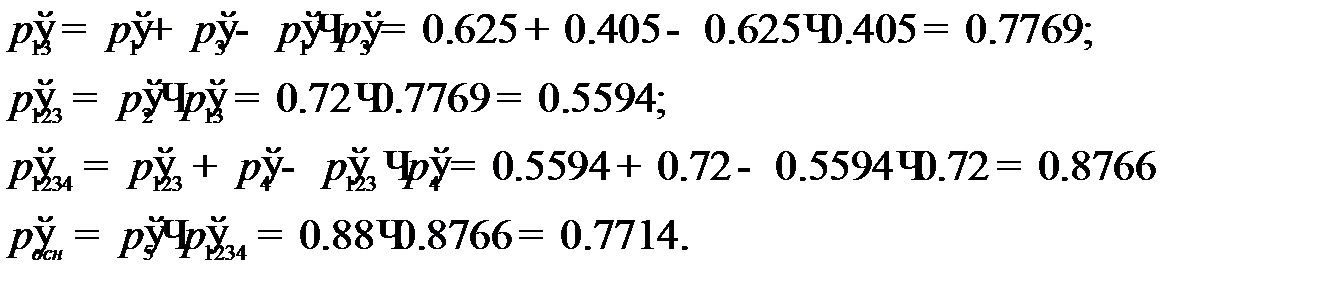
Надёжность меньше 0,95.
Повторим резервирование.
| Элемент | |||||
| Надёжность | 0.6250 | 0.7200 | 0.4050 | 0.7200 | 0.8800 |
| Надёжность резервирующего элемента | 0,3711 | 0,4104 | 0,2627 | 0,4104 | 0,4664 |
| Надёжность резервированного элемента | 0,7422 | 0,8208 | 0,5255 | 0,8208 | 0,9328 |
Рассчитываем надёжность цепи после двукратного резервирования, используя надёжности из таблицы.
Надёжность всё ещё меньше 0,95.
Повторим резервирование ещё раз.
| Элемент | |||||
| Надёжность | 0,7422 | 0,8208 | 0,5255 | 0,8208 | 0,9328 |
| Надёжность резервирующего элемента | 0,4189 | 0,4472 | 0,3251 | 0,4472 | 0,4821 |
| Надёжность резервированного элемента | 0,8379 | 0,8943 | 0,6502 | 0,8943 | 0,9641 |
Рассчитываем надёжность цепи после трёхкратного резервирования, используя надёжности из таблицы.
Надёжность всё ещё меньше 0,95.
Повторим резервирование.
| Элемент | |||||
| Надёжность | 0,8379 | 0,8943 | 0,6502 | 0,8943 | 0,9641 |
| Надёжность резервирующего элемента | 0,4529 | 0,4708 | 0,3819 | 0,4708 | 0,4907 |
| Надёжность резервированного элемента | 0,9058 | 0,9416 | 0,7639 | 0,9416 | 0,9814 |
Рассчитываем надёжность цепи после четырёхкратного резервирования, используя надёжности из таблицы.
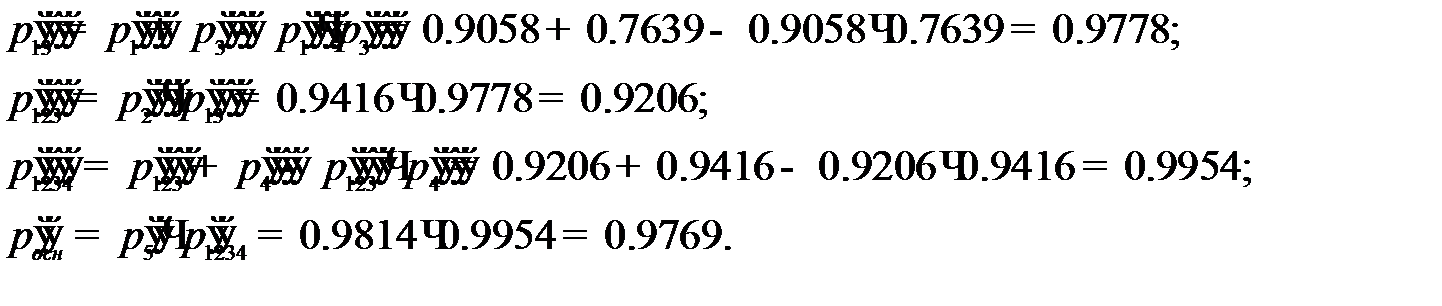
Надёжность больше 0,95.
Резервирование выполнено.
Общее резервирование предполагает, что при отказе любого элемента основной цепи включается резервная цепь, которая полностью заменяет основную.
Вычислим надёжность резервной схемы.
Проведём резервирование резервной схемой.
Надёжность системы при однократном резервировании равна
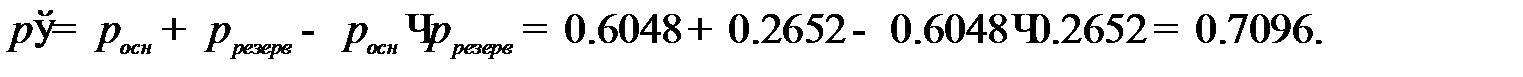
Надёжность меньше 0,95. Повторим резервирование.
Надёжность системы при двукратном резервировании равна
.
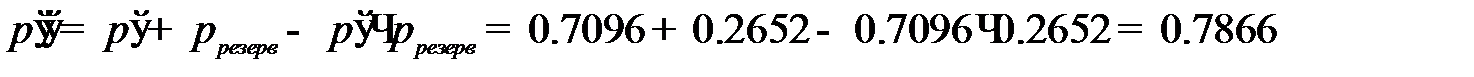Надёжность меньше 0,95. Повторим резервирование.
Надёжность системы при трёхкратном резервировании равна
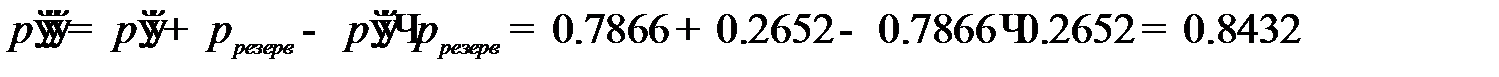
Надёжность меньше 0,95. Повторим резервирование.
Надёжность системы при четырёхкратном резервировании равна
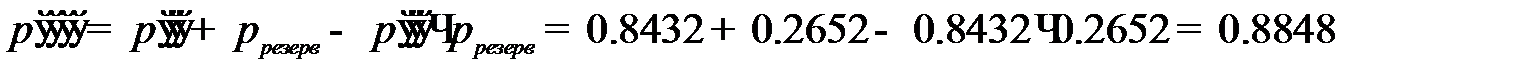Надёжность меньше 0,95. Повторим резервирование.
Надёжность системы при пятикратном резервировании равна
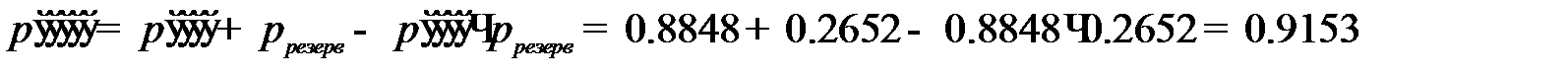
Продолжаем…
Надёжность системы при шестикратном резервировании равна
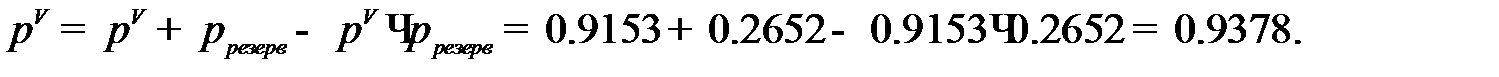Надёжность системы при семикратном резервировании равна
Надёжность больше 0,95.
Резервирование выполнено.
Выводы по этапу 1.
При раздельным резервировании каждый элемент основной схемы был резервирован элементом половинной надёжности.
При общем резервировании схема была резервирована 7-ю резервными схемами по 4 элемента.
В основной схеме 5 элементов. Таким образом, для резервирования её методом раздельного резервирования с надежностью 0,95 необходимо 20 резервных элементов.
В резервной схеме 4 элемента. При семикратном резервировании используется также 28 резервных элементов.
| Метод | Число резервных элементов |
| Раздельное резервирование | |
| Общее резервирование |
Таким образом, предпочтительно раздельное резервирование.
Этап 2
Теоретическая часть
Дискретной называют такую случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Примерами могут послужить денежный выигрыш в лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения: непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей должна равняться 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)).
Закон распределения может быть задан следующей таблицей:
| Значения хi | x1 | x2 | x3 | … | xn |
| Вероятности pi | p1 | p2 | p3 | … | pn |
События X = xi (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Следовательно, сумма их вероятностей равна единице: р1+р2+р3+…+рn = 1.
Функция распределения случайной величины - это вероятность того, что случайная величина (для удобства назовём её ξ) примет значение меньшее, чем какое-то конкретно заданное числовое значение x: F(X) = P(ξ<X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины.
Далее рассмотрим основные числовые характеристики дискретных случайных величин:
§ Математическое ожидание дискретной случайной величины равно сумме произведений всех значений, которые принимает случайная величина на соответствующие вероятности: M(X)=Σxipi. Для биномиального распределения M(X) = np, для распределения Пуассона M(X) = λ
§ Дисперсия дискретной случайной величины есть разность математического ожидания случайной величины, возведённой в квадрат, и квадрата математического ожидания: D(X) = M[X–M(X)]2 = M(X2)−[M(X)]2. Здесь разность X–M(X) - отклонение случайной величины от ее математического ожидания. Для биномиального распределения D(X) = npq, для распределения Пуассона D(X) = λ
§ Среднее квадратическое отклонение дискретной случайной величины можно посчитать как квадратный корень из дисперсии: σ(X) = √D(X)
Функция распределения дискретной случайной величины является ступенчатой, причем в точках разрыва величины скачков равны вероятностям соответствующих реализаций случайной величины Х:
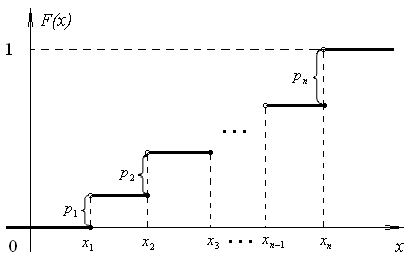
Функция распределения обладает следующими свойствами.
1. Функция распределения заключена между нулем и единицей, поскольку она определена как вероятность случайного события.
2. Вероятность попадания случайной величины в интервал равна разности значений функции распределения на концах этого интервала. Отсюда следует, что вероятность отдельного значения непрерывной случайной величины равна нулю.
3. Функция распределения случайной величины не убывает.
4. На минус бесконечности функция распределения равна нулю, а на плюс бесконечности - единице.
Статистический ряд часто оформляется графически в виде так называемой гистограммы, которая служит графической иллюстрацией для непрерывного признака.
Практическая часть
Исходные данные:
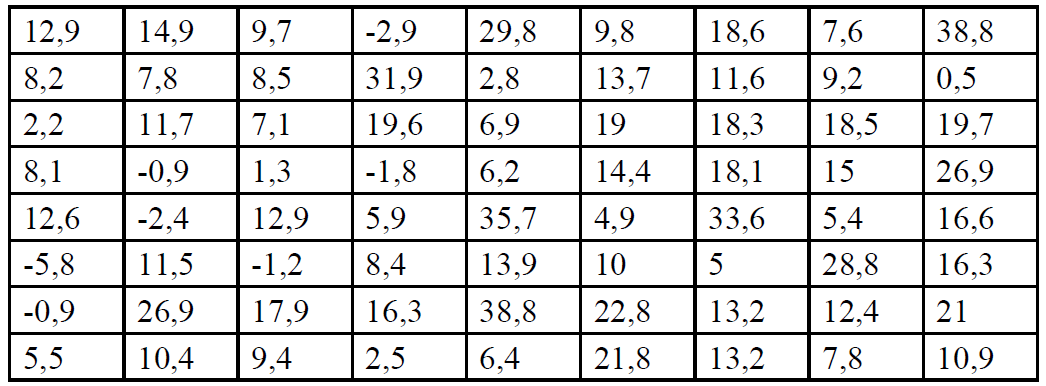
1. Найти статистические оценки числовых характеристик случайной величины Х.
Числовые характеристики
Выборочное среднее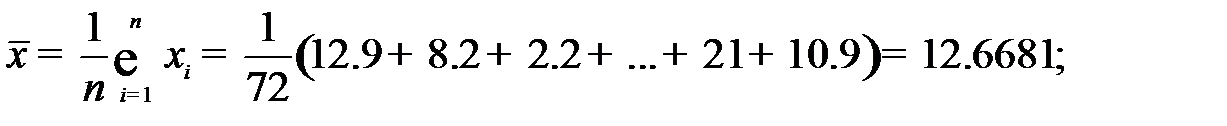 
Выборочная дисперсия 
Несмещённая оценка
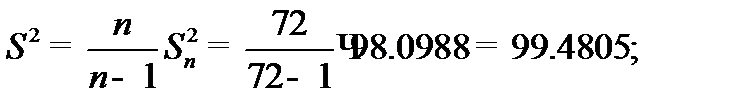
Среднеквадратическое отклонение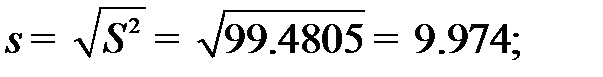 
.
Мода — значение в выборке, которое встречается наиболее часто,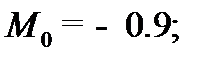 
.
Медиана — число, характеризующее выборку (например, набор чисел) — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него,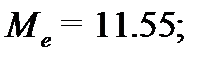 
2. Построить интервальный статистический ряд распределения случайной величины Х и соответствующую функцию распределения F(x), построить гистограмму.
Объём выборки N=72;
Находим число интервалов по формуле Стёрждесса.
Максимальный и минимальный элементы и шаг интервала:
Размах
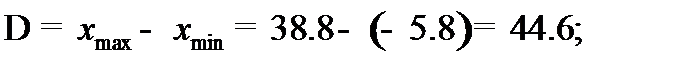
Шаг интервала
Интервальный статистический ряд
| Интервалы | -5.8000 0.5714 | 0.5714 6.9429 | 6.9429 13.3143 | 13.3143 19.6857 | 19.6857 26.0571 | 26.0571 32.4286 | 32.4286 38.8 |
| Абсолютная частота, | |||||||
| Относительная частота, | 0.1111 | 0.1667 | 0.3333 | 0.2083 | 0.0556 | 0.0694 | 0.0556 |
| Накопленная частота | |||||||
| Накопленная относительная частота | 0.1111 | 0.2778 | 0.6111 | 0.8194 | 0.8750 | 0.9444 |
Высота столбцов гистограммы: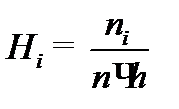 
.
| Интервалы | -5.8000 0.5714 | 0.5714 6.9429 | 6.9429 13.3143 | 13.3143 19.6857 | 19.6857 26.0571 | 26.0571 32.4286 | 32.4286 38.8 |
Высота столбцов гистограммы,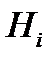 
| 0.0174 | 0.0262 | 0.0523 | 0.0327 | 0.0087 | 0.0109 | 0.0087 |
3. По виду гистограммы сформулировать гипотезу о теоретическом законе распределения.
Можно выдвинуть гипотезу о нормальном распределении выборки.
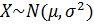
4. Используя методы максимального правдоподобия или моментов, найти оценки параметров выбранного закона распределения и вычислить их.
Плотность вероятности:
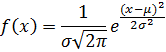
Функция вероятности:
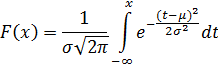
Составим функцию правдоподобия
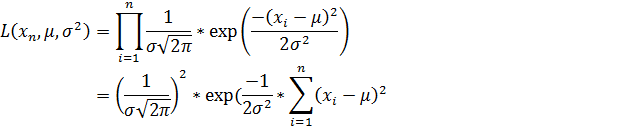
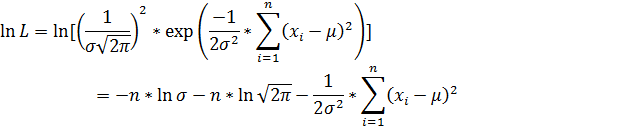
Находим частные производные
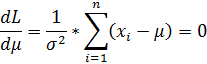
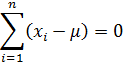
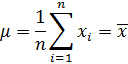
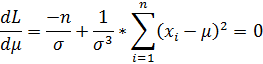
Приходим к выводу, что:
5. Теоретические законы распределения f(x), F(x) построить вместе с гистограммой и статистической функцией распределения F(x).
Выводы по этапу 2.
Проведя необходимые расчеты, было вычислено
· выборочное среднее
· выборочная дисперсия
· несмещенная оценка
· среднеквадратичное отклонение
· мода
· медиана
Построен интервальный статистический ряд распределения случайной величины Х, соответствующая функция распределения F(x), построена гистограмма.
На основании этого сделан вывод о том, что распределение нормальное.
Используя методы максимального правдоподобия, найдены оценки параметров выбранного закона распределения и вычислены.
Построены графики теоретической плотности и теоретической функции вероятности.
В результате расчётов было установлено, что выдвинутая гипотеза о нормальном законе распределения случайной величины X соответствует экспериментальным данным.
Список использованной литературы
1. Кибзун А.И., Горяинова Е.Р., Наумов А.В. «Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами: Учебник. – 3-е изд., перераб. и доп. — М.: Физматлит, 2013.-232с.
2. Захаров В.К., Севастьянов Б.А., Чистяков В.П. «Теория вероятностей» — М.: Наука, 1983.
3. Пугачев В.С. «Теория вероятностей и математическая статистика» — М.: Наука, 1979.
4. Кочетков Е.С., Смерчинская С.О. «Теория вероятностей в задачах и упражнениях» —М.: Форум, 2008.