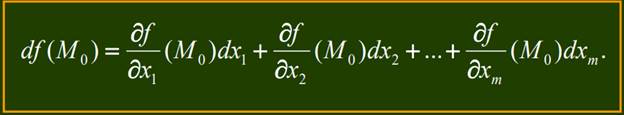ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Частные производные. Пусть функция u = f(x1, x2,..., xm) определена в окрестности точки М. Пусть x1 – переменная величина, а x2= x2 0,..., xm= xm 0. Тогда эта функция, рассматриваемая как функция от x1, может иметь производную в точке x1 0. По определению такая производная называется частной производной по переменной x1 и обозначается
Определение дифференцируемости функции двух переменных в точке.
ОПРЕДЕЛЕНИЕ. Функция z = f(М) = f(x, y) называется дифференцируемой в точке M0 (x0, y0), если она определена в некоторой окрестности этой точки и существуют такие числа А1, А2, что полное приращение функции в этой точке представимо в виде Df = f(x0+Dx, y0+Dу) – f(x0, y0)= А1Dx + А2Dу + a1 (Dx, Dy)Dx+a2 (Dx, Dy)Dy, где a1 (Dx, Dy), a2 (Dx, Dy) – бесконечно малые при Dx®0, Dy®0 функции.
Дифференциалом df дифференцируемой в точке M0 (x0, y0) функции z =f(М) = f(x, y) называется главная, линейная относительно приращений аргументов часть приращения этой функции в точке M0 (x0, y0), то есть df(M0)= А1Dx+ А2Dу.
Другая форма условия дифференцируемости.
Рассмотрим бесконечно малую при Dx®0, Dy®0 функцию 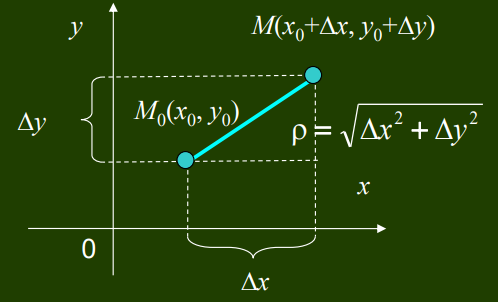
a1 (Dx, Dy)Dx+a2 (Dx, Dy)Dy = о(ρ) и условие дифференцируемости может быть записано так: Df = f(x0+Dx, y0+Dу) – f(x0, y0)= А1Dx + А2Dу + о(ρ) при Dx®0, Dy®0
Определение дифференцируемости функции m переменных в точке.
Функция u = f(М) = f(x1, x2,..., xm) называется дифференцируемой в точке М0 (х1 0, х2 0,..., хm 0) Î Rm, если она определена в некоторой окрестности этой точки и существуют такие числа А1, А2,..., Аm, что полное приращение функции в этой точке представимо в виде Df = f(М) – f(М0)= А1 Dx1+ А2Dx2 +... +АmDxm + a1Dx1+ a2Dx2 +... + amDxm, где a1, a2, …, am – бесконечно малые при Dx1→ 0, Dx2→ 0, …, Dxm→ 0 функции. Дифференциалом df дифференцируемой в точке M0 функции u = f(М) называется главная, линейная относительно приращений аргументов часть приращения этой функции в точке M0, то есть df(M0)= А1Dx1+ А2Dx2 +... +АmDxm.
Необходимое условие дифференцируемости.
ТЕОРЕМА. Если функция u = f(x1, x2,..., xm) дифференцируема в точке М0 (х1 0, х2 0,..., хm 0) Î Rm, то она имеет в этой точке все частные производные и ее дифференциал равен 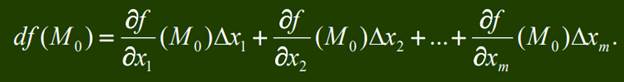
Доказательство. Приведем доказательство для функции двух переменных z = f(x, y). Пусть сначала Dу = 0. Тогда условие дифференцируемости функции в точке M0 (x0, y0) принимает вид: Df = f(x0+Dx, y0) – f(x0, y0) = А1Dx + a1 (Dx)Dx, откуда вытекает, что
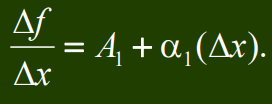
Переходя к пределу при Dx®0 и учитывая, что 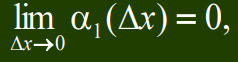
Получим 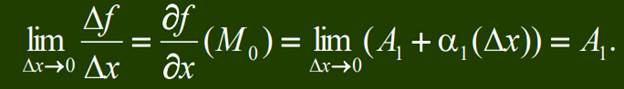
Таким образом 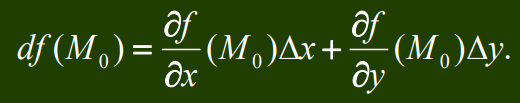
Связь между дифференцируемостью функции в точке и непрерывностью.
ТЕОРЕМА. Если функция u = f(x1, x2,..., xm) дифференцируема в точке М0 (х1 0, х2 0,..., хm 0) Î Rm, то она непрерывна в этой точке.
Достаточные условия дифференцируемости функции в точке.
ТЕОРЕМА. Если функция u = f(x1, x2,..., xm) имеет частные производные по всем переменным в некоторой окрестности точки М0, непрерывные в этой точке, то функция дифференцируема в точке М0.
Полное приращение функции представим в виде Df = f(x0+Dx, y0+Dу) – f(x0, y0+Dу)) + + (f(x0, y0+Dу) – f(x0, y0).
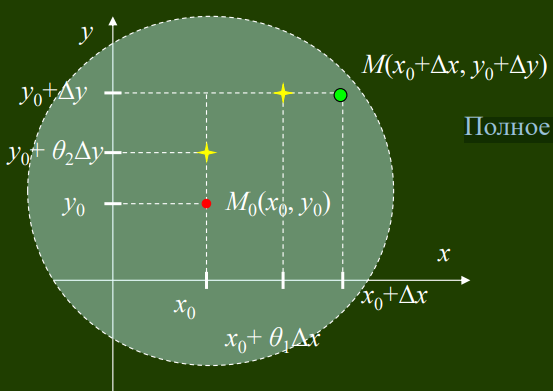
Зафиксировав y0+Dу, применим формулу конечных приращений Лагранжа к функции f(x,y0+Dу)одной переменной х на отрезке [x0, x0+Dx]: 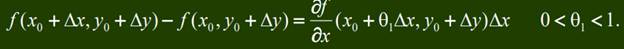
ЗАМЕЧАНИЕ. Эта теорема имеет важное значение для установления дифференцируемости функции, так как проверка непрерывности ЧП часто оказывается проще непосредственной проверки дифференцируемости по определению. Обозначим dx1 = Dx1, dx2 = Dx2, …, dxm = Dxm – дифференциалы независимых переменных. В этих обозначениях дифференциал функции u = f(x1, x2,..., xm) записывается в виде